Систематический помехоустойчивый код. Построение систематического кода.
Систематический код – это групповой n-значный код в котором k символов является информационными, а n-k являются проверочными, избыточными. Они занимают одни и те же позиции. Задание СК производится с помощью производящей матрицы А и проверочной матрицы Н.
Производящая матрица позволяет получить все комбинации кода путем суммирования по модулю 2.
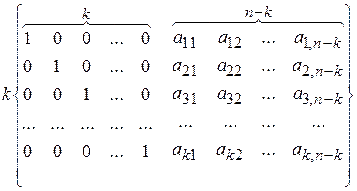
(n-k) разрядные кодовые комбинации, в которых количество единиц не менее чем dmin-1, а сумма любых двух строк по модулю 2 должна содержать не менее чем dmin-2«единиц». Желательно при этом, чтобы единицы чередовались с нулями, чтобы серии единиц были короткие. 2k – число кодовых комбинации.
Структура производящей матрицы позволяет строить систематический код, у которого первые k-позиции будут информационными, а оставшиеся (n-k) проверочные, при этом общее число разрешенных кодовых комбинаций равно 2k и все различные кодовые комбинации могут быть получены в результате линейной операции суммы по |2| любых двух, трех и более строк производящей матрицы.
Построение проверочной матрицы:
Берем единичную матрицу размерности n-k и слева к ней приписывают транспонированную дополнительную матрицу D, которую использовали для построения производящей матрицы А.
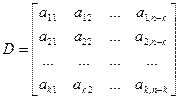 ,
, 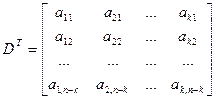

Таким образом, проверочная матрица H позволяет построить алгоритм кодирования и декодирования систематического кода, исходя из того, что единица в каждой строке соответствует тем разрядам, сумма которых по модулю 2 должна быть равна нулю.
Из проверочных уравнений выделяют проверочные разряды, количество которых равно n-k. Проверочные разряды встречаются в каждом из проверочных уравнений только по одному разу.
Процесс приема-передачи с корректировкой ошибок:
Формируется информационная часть кодовой комбинации. На ее основе строится проверочная часть с помощью проверочных уравнений.
На приемной стороне полученные разряды подставляются в проверочные уравнения. Если кодовая комбинация передана без ошибки, то все проверочные уравнения примут нулевые значения.
Если какие либо уравнения примут ненулевое значение, тогда формируют опознаватель для обнаружения и исправления ошибок.
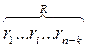
Если вектор-опознаватель не равен нулю, тогда производится обнаружение ошибочных разрядов следующим образом:
доказано, что вектор-опознаватель совпадает со значением «правой части» производящей матрицы, если кратность ошибки равна 1.
Если кратность ошибки больше 1, тогда ошибочные разряды могут быть обнаружены следующим образом: формируется сумма по модулю 2 из «правых частей» строк проверочной матрицы. Количество различных строк, которые включаются в сумму по модулю 2 определяют кратность ошибки.