Действия с матрицами

Прямоугольная таблица чисел, содержащая m строк и n столбцов, называется матрицей размера m´n:

.

Каждый элемент матрицы снабжается двумя индексами: первый указывает номер строки, второй – номер столбца, в которых расположен этот элемент.

Две матрицы называются равными, если числа их строк и столбцов равны и если равны элементы, расположенные на соответствующих местах этих матриц.

Если число столбцов матрицы n равно числу ее строк, то матрицу называют квадратной матрицей порядка n. Элементы , , 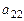, 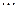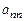квадратной матрицы порядка n образуют ее главную диагональ.

Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю.

Диагональная матрица Е называется единичной, если все ее элементы, расположенные на главной диагонали, равны единице.

Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число.

Суммой матриц A и B одинаковых размеров называется матрица, элементы которой равны суммам элементов матриц A и B, расположенных на соответствующих местах:

+ =

= .

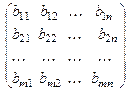Матрицу 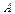можно умножить на матрицу только в том случае, когда число столбцов матрицы равно числу строк матрицы . В результате умножения получится матрица 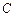, у которой столько же строк, сколько их в матрице , и столько же столбцов, сколько их в матрице . Элементы матрицы 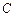вычисляются по формуле

,

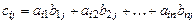т.е. для получения элемента 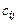, расположенного в i-й строке и j-м столбце матрицы c, надо элементы i-й строки матрицы A умножить на соответствующие элементы j -го столбца матрицы B и полученные произведения сложить:

Пример.

= .
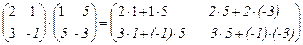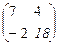