Алгоритм

1. Одним простым вращением нельзя прямую общего положения поставить в положение проецирующей, поэтому сначала решают задачу №1: прямую СD поставить в положение горизонтали.

2. Выбираем ось вращения i ^ П₂; i É С (рис. 4-48, б)

3. Радиус вращения: R = | С₂D₂ |

4. Вращаем C₂D₂ вокруг оси i₂ = C₂ до положения, когда C₂D₂ станет ^ C₁C₂ (рис. 4-48 в).

5. Точка C₁ останется на оси i₁, все другие точки прямой переместятся по прямым, перпендикулярным линиям связи. Точка D₁ переместится в положение D₁’

6. Отрезок CD’ - горизонталь Þ | CD | = | C₁D₁’ | (рис. 4-48, г)

7. Угол b - угол наклона CD к П₂.

а) CD – прямая общего положения

б)

в) Прямая CD заняла положение горизонтали

г) CD(CD’) - горизонталь

Рис. 4-48

8. Проводим второе вращение. Ось i² выбираем ^ П₁, i ² É D¹; i₁² = D₁¹; i₂² || D₁¹D₂¹ (рис. 4-49а);

9. Радиус вращения: R = | C₁D₁¹ |.

10. Вращаем C₁D₁¹ до положения, когда C₁D₁¹ станет || линиям связи, и станет равной С₁²D₁¹ (точка D₁¹ не вращается).

11. Точка С₂, двигаясь по прямой, займет положение D₂¹, т.е. С₂² = D₂¹ (рис. 4-49 в)

12. Отрезок С²D¹ - проецирующий, С²D¹ ^^ П₂ .

13. Общий вид решения показан на рис. 4-49 б.

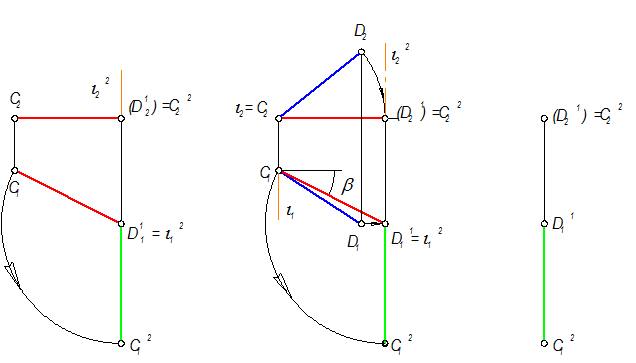
а) Задача №2

б) Задача №1 и №2

в) CD(C2D1) – проецирующая прямая

Рис. 4-49