Взаимная перпендикулярность двух прямых общего положения

Задача: Через точку К, взятую на прямой общего положения m, провести прямую n, тоже общего положения, перпендикулярную m (рис. 4-15).

Рис. 4-15

Так как прямой угол между прямыми общего положения искажается на обеих плоскостях проекций, то решение задачи на построение взаимно перпендикулярных прямых приходится сводить к задаче на построение взаимно перпендикулярных прямой и плоскости.

При этом используется известное положение, что две прямые перпендикулярны в том, и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.

Алгоритм решения:

1. Через точку К проводим плоскость S, перпендикулярную прямой m. Плоскость задаём пересекающимися горизонталью и фронталью (рис. 4-16), причём, h₁ ^ m₁, a f₂ ^ m₂.

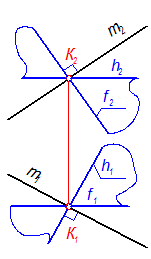
Рис. 4-16

2. Так как плоскость S(h Ç f) ^ m, то в этой плоскости можно взять некоторую прямую общего положения n, проходящую через точку К (рис. 4-17). Она будет перпендикулярна m. Задаём n₁.

Рис. 4-17

3. Известно, что прямую определяют две точки. На n₁, кроме К₁, возьмём ещё одну точку Р₁.

4. Находим n₂ в плоскости S. Для этого проводим в этой плоскости прямую 12(1₁ -2₁). Точка Р₁ принадлежит этой прямой, а, следовательно, плоскости S. Находим Р₂ и проводим прямую n₂

Алгоритмическая запись решения:

1. S ^ m, S = h Ç f = K; h ^ m Þ h₁ ^ m₁, h₂ ^ K₂K₁; f ^ m Þ f₂ ^ m₂, f₁ ^ K₂K₁;

2. n = PK, n Ì S, n₁ = P₁K₁; P₁ Î 1₁2₁ Þ P₁ Î S Þ P₂ Þ n₂.

3. n Ì S Þ n ^ m.