Взаимная перпендикулярность прямой и плоскости.

Из элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Задача: Через точку К Î S построить прямую n, перпендикулярную плоскости S(а || b). Анализ решения задачи проведём на пространственном чертеже, рис. 4-2.

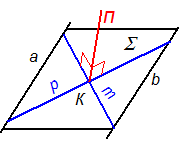
Чтобы провести прямую n ^ S, нужно в этой плоскости взять две пересекающиеся прямые (на рис. 4-2 это р Ç m = К). Прямую n нужно строить перпендикулярно одновременно двум этим прямым.

Однако, если прямые р и m будут прямыми общего положения, то прямой угол к ним ни на одной плоскости проекций не спроецируется в натуральную величину. Согласно теореме опроецировании прямого угла (см. свойство 2 ортогонального проецирования, модуль №1) прямой угол спроецируется в натуральную величину на какую-нибудь плоскость проекций, если одна сторона прямого угла будет параллельной этой плоскости проекций. Поэтому, в качестве прямых р и m выгодно взять горизонталь h и фронталь f (рис. 4-3). Тогда прямой угол между n и h спроецируется в натуральную величину на П₁, а прямой угол между n и f - на П₂.

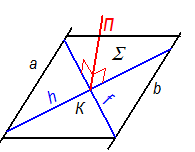
Рис. 4-3

Плоский чертёж: На рис. 4-4 плоскость S задана параллельными прямыми а и b. Точка К(К₂) принадлежит этой плоскости. Нужно построить n ^ S, n Î К.

Рис. 4-4

Согласно приведённым выше рассуждениям, в плоскости необходимо взять горизонталь и фронталь, затем, перпендикулярно каждой из них строить п. Построения начинаем с горизонтали (рис. 4-5).

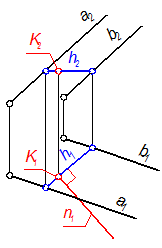
Рис. 4-5

Через точку К₂ проводим h₂ ^ линиям связи, находим h₁, а на ней, с помощью линии связи, К₁. Так как n ^ h, то n₁ ^ h₁, поэтому проводим n₁ ^ h₁ через точку K₁.

Аналогично находим n₂ (рис. 4-6). Через точку К₁ проводим f₁ ^ линиям связи, находим f₂. Так как n ^ f, тo n₂ ^ f₂, поэтому проводим n₂ ^ f₂ через точку К₂.

Рис. 4-6

Полностью решение задачи представлено на рис. 4-7. Видимость прямой n не учитывалась.

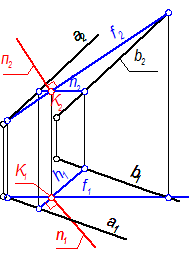
Рис. 4-7

Алгоритмическая запись решения:

1. h Ì S, f Ì S, h Ç f = K.

2. K Î n Þ K₁ Î n₁, K₂ Î n₂.

3. n ^ h Þ n₁ ^ h₁;

4. n ^ f Þ n₂ ^ f₂.

 

Итак, чтобы задать на комплексном чертеже прямую n, перпендикулярную данной плоскости S, достаточно построить n₁ и n₂, расположив их в любом месте чертежа, чтобы n₁^h₁, n₂ ^ f₂, где h и f - горизонталь и фронталь плоскости, при условии, что h Ç f.

 

Если плоскость S занимает проецирующее положение, то прямая, перпендикулярная ей, является линией уровня (рис. 4-8, 4-9).

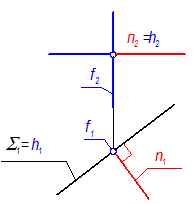
Рис. 4-8

Если S - горизонтально проецирующая:

S ^^ П₁ Þ h₁ = S₁, f ^^ П₁

n ^ h Þ n₁ ^ h₁; n ^ f Þ n₂ ^ f ₂; Þ n - горизонталь

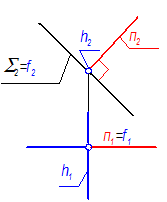
Рис. 4-9

Если S - фронтально проецирующая:

S ^^ П₂ Þ f₂ = S₂, h ^^ П₂.

n ^ h Þ n₁ ^ h₁; n ^ f Þ n₂ ^ f₂; Þ n -фронталь

 

Чтобы лучше понять данное утверждение, нужно вспомнить , какие прямые являются линиями уровня в проецирующих плоскостях. Для этого посмотрите рис. 2-12 и 2-14 в модуле № 2.