Шесть функций денежной единицы.
Суть оценки стоимости приносящего прибыль проекта состоит в том, что определяется текущая стоимость прибыли, которая будет получена в прогнозируемом периоде. Гривна, полученная завтра, стоит меньше, чем гривна полученная сегодня. Это обусловлено тем, что деньги со временем приносят доход; а во-вторых - инфляционные процессы обесценивают деньги. В связи с этим рассмотрим шесть функций денежной единицы, которые отражают текущую стоимость денег.
Первая (прямая) функция. Накопление суммы денежной единицы: будущая стоимость денежной единицы.
При расчете будущей стоимости денежной единицы используется обычная формула сложного процента, которая позволяет рассчитывать и учитывать процент на вложенный процент:
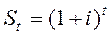 , где
, где
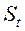 – депозитная сумма после t периодов, если вложен 1 долл.; 1 – один доллар; i – периодическая ставка процента; t – число периодов.
– депозитная сумма после t периодов, если вложен 1 долл.; 1 – один доллар; i – периодическая ставка процента; t – число периодов.
Существую специальные таблицы шести функций денежной единицы, содержащие предварительно рассчитанные элементы (отдельные множители) сложного процента, но можно рассчитывать их и самим.
На рис. 9.1 представлена диаграмма возрастания во времени текущей стоимости, положенной на депозит, по сложному проценту.
 | |||
|
Данные о накопленной сумме в 1 доллар по сложному проценту при ставке 10% и ежегодном накоплении.
| Год (t) | Накопленная сумма (St) | Год (t) | Накопленная сумма (St) |
| 1,10 | 1,9487 | ||
| 1,21 | 2,1436 | ||
| 1,331 | 2,3579 | ||
| 1,4642 | 2,5937 | ||
| 1,6105 | 6,7275 | ||
| 1,7716 | 17,4494 |
Накопление денежных средств может происходить более часто, чем год: ежедневно. Ежемесячно, ежеквартально или каждое полугодие. При более частом накоплении денежных средств эффективная ставка снижается. Расчет производится по основной формуле сложного процента с определенной ее корректировкой: число лет (t), на протяжении которого происходит накопление, умножается на частоту накопления в течение года, а номинальная годовая ставка процента делится на частоту накопления.
Вторая (обратная) функция сложного процента: текущая стоимость денежной единицы.
Текущая стоимость денежной единицы (стоимость реверсии, V) – это величина, обратная накопленной сумме единицы:
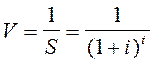
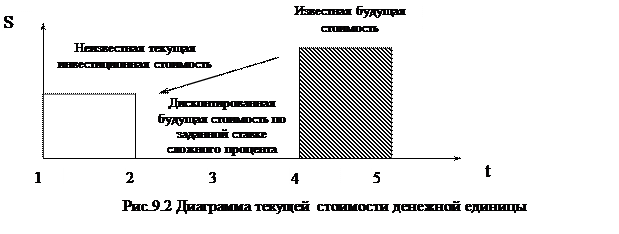
Текущая стоимость денежной единицы – это текущая стоимость одного доллара, которая будет получена в будущем. Диаграмма текущей стоимости денежной единицы показана на рис. 9.2.
 |
Коэффициент текущей стоимости денежной единицы используется для оценки текущей стоимости известного (или прогнозируемого) единовременного поступления денежных средств с учетом заданного процента (с учетом ставки дисконта).
Допустим, инвестору необходимо определить, сколько нужно заплатить сегодня за оцениваемое предприятие, чтобы получить от него доход в 10% годовых, а через 2 года его продать, например за 10 млн. долл. Если инвестор собирается получить 10% на вложенный капитал, то сумма, которую он может предложить за предприятие сегодня:  млн. долл.
млн. долл.
Механизм определения коэффициента текущей стоимости денежной единицы при годовой ставке дисконта 10%.
| Год (t) | Накопленная сумма (St) | Обратная величина | Текущая стоимость единицы (V) |
| 1,10 | 1/1,10 | 0,9091 | |
| 1,21 | 1/1,21 | 0,8264 | |
| 1,331 | 1/1,331 | 0,7512 | |
| 1,4642 | 1/1,4642 | 0,6830 | |
| 1,6105 | 1/1,6105 | 0,6209 |
Третья (прямая) функция сложного процента: текущая стоимость единичного аннуитета.
Аннуитет (обычный) – серия равновеликих платежей, первый из которых осуществляется через один период, начиная с настоящего момента, то есть платеж производится в конце рассматриваемых периодов.
На рис.9.3 представлена диаграмма текущей стоимости обычного аннуитета, то есть текущая стоимость серии равновеликих платежей.
 |
Такая ситуация может возникнуть, если собственник сдает активы предприятия в аренду и хочет получать ежегодную арендную плату в 100 тыс. долл. в течение следующих четырех лет. При 10% ставке дисконта текущая стоимость первого арендного платежа в 100 тыс. долл. через год равна 90,91 тыс. долл. (100 тыс. долл. * 0,9091=90, 91 тыс. долл.), второго арендного платежа – 82,64 тыс. долл. (100 тыс. долл. * 0,8264=82, 64 тыс. долл.), третьего арендного платежа – 75,13 тыс. долл., четвертого - 63,30 тыс. долл. Таким образом, текущая стоимость арендных платежей в 100 тыс. долл. в течение 4 последующих лет при ставке 10% составляет 316,98 тыс. долл.
Текущая стоимость аннуитета (at) может быть рассчитана как сумма текущих стоимостей 1 долл. за определенный период времени:

Для построения таблицы обычного аннуитета необходимо сложить данные текущей стоимости единицы за соответствующее число лет.
Если периодические платежи поступают чаще, чем один раз в год, номинальную (годовую) ставку процента необходимо разделить на число периодов в году. Общее число периодов равно числу лет, умноженному на число периодов в году.
Если собственник договаривается с арендатором о том, что он (арендатор) будет осуществлять равномерные авансовые платежи по следующей схеме: первый платеж немедленно после подписания контракта, а последующие равные платежи через определенный период, то такие платежи называются авансовым аннуитетом.
Четвертая (обратная) функция сложного процента: взнос на амортизацию денежной единицы.
Взнос на амортизацию денежной единицы – это регулярный периодический платеж в погашение кредита, приносящего процентный доход. Это величина, обратная текущей стоимости аннуитета.
Амортизация в данном случае – это погашение (возмещение, ликвидация) долга в течение определенного времени. Взнос на амортизацию кредита математически определяется как отношение одного платежа к первоначальной основной сумме кредита. Взнос на амортизацию единицы равен обязательному периодическому платежу по кредиту, включающему процент и выплату части основной суммы. Это позволяет погасить кредит и проценты по нему в течение установленного срока.
1 долл., ожидаемый к получению в конце каждого года на протяжении 4 лет, имеет при годовой ставке 10% текущую стоимость 3,1698. Это текущая стоимость аннуитета.
Величина взноса на амортизацию равна обратной величине текущей стоимости аннуитета, то есть взнос на амортизацию 1 долл. составляет величину, обратную 3,1698 долл.
Математическое отношение одного платежа к первоначальной основной сумме кредита составляет

Эта величина показывает размер периодического ежегодного платежа для погашения задолженности по кредиту 3,1698 долл. в течение 4 лет при ставке 10%.
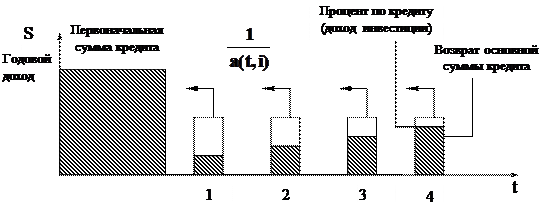 Каждый взнос на амортизацию единицы включает процент и выплату части первоначальной основной суммы кредита. Соотношение этих составляющих изменяется с каждым платежом (рис. 9.4).
Каждый взнос на амортизацию единицы включает процент и выплату части первоначальной основной суммы кредита. Соотношение этих составляющих изменяется с каждым платежом (рис. 9.4).
Рис.9.4 Взнос на амортизацию единицы
Для определения взноса на амортизацию денежной единицы используется следующая формула:
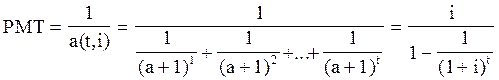
Пятая (прямая) функция сложного процента: накопление (рост) единицы за период - будущая стоимость аннуитета.
Фактор накопления единицы позволяет ответить на вопрос о том, какой по истечению всего срока будет стоимость серии равных взносов, депонированных в конце каждого из периодических интервалов.
Например, предприниматель хочет накопить определенную сумму для покупки нового станка. Станок стоит 4,641 долл. Он в конце каждого года откладывает на депозит по 1 долл., который приносит 105-ный годовой доход. К концу четвертого года он скапливает необходимую сумму (4,641 долл.) и покупает станок.
Расчет накопления единицы за период S(t,i) осуществляется по следующей формуле:

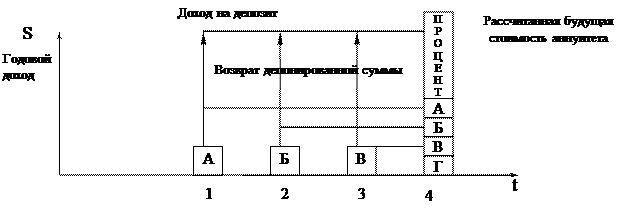
Рис.5 Накопление единицы за период
Шестая (обратная) функция сложного процента: фактор фонда возмещения.
Фактор фонда возмещения показывает сумму, которую нужно депонировать в конце каждого периода (периодический депозит), чтобы через заданное число периодов остаток на счете составил 1 долл. При этом учитывается процент, получаемый по депозитам.
Например, предпринимателю необходимо за четыре года скопить 4,641 долл. для покупки станка. Какие суммы денег ему необходимо откладывать каждый год при 10% годовых, чтобы через 4 года купить этот станок?
Ответ: ежегодный вклад должен составить 1 долл. (0,215471*4,641=1 долл.).
Фактор фонда возмещения – это величина обратная фактору накопления денежной единицы за период:

 |
Рис.5 Фактор фонда возмещения
Взаимосвязи между функциями сложного процента.
Все шесть функций сложного процента строятся с использованием общей базовой формулы сложного процента (1+i)t, характеризующей накопленную сумму единицы. Все пять функций сложного процента являются производными от первой (прямой) функции сложного процента – накопленной функции единицы (будущая стоимость единицы). Каждая из функций предполагает, что деньги положенные на депозит, до тех пор, пока находятся на нем, приносят процент. В основу каждого фактора положен эффект сложного процента, при котором процент переводится в основную сумму (табл.9.2).
Таблица 9.2 Взаимосвязь между функциями сложного процента