Метод Ньютона.
Как было отмечено в п. 2.1, задача одномерной оптимизации дифференцируемой функции  сводится к нахождению критических точек этой функции, определяемых уравнением
сводится к нахождению критических точек этой функции, определяемых уравнением
 (2.7)
(2.7)
Когда уравнение (2.7) нельзя решить аналитически, для его решения можно применить численные методы, например метод Ньютона. В этом случае говорят о методе Ньютона решения задачи оптимизации.
Пусть  - решение уравнения (2.7), а
- решение уравнения (2.7), а  некоторое начальное
некоторое начальное
приближение к  . Применим для решения (2.7) метод Ньютона решения уравнения
. Применим для решения (2.7) метод Ньютона решения уравнения  , которое эквивалентно уравнению (2.7) при
, которое эквивалентно уравнению (2.7) при  . Для этого в формулу для
. Для этого в формулу для  -го приближения метода Ньютона
-го приближения метода Ньютона

подставим вместо  производную
производную 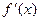 и получим тем самым формулу для
и получим тем самым формулу для  -го приближения к решению уравнения (2.7):
-го приближения к решению уравнения (2.7):
 (2.8)
(2.8)
для использования этой формулы необходимо, чтобы  . В качестве критерия окончания итерационного процесса можно применить условия близости двух последовательных приближений
. В качестве критерия окончания итерационного процесса можно применить условия близости двух последовательных приближений

или близости значений целевой функции на этих приближениях
 .
.
Достаточное условие сходимости метода Ньютона (2.8) можно получить. А именно, справедлива следующая теорема.
Теорема. Пусть  - корень уравнения (2.7), т.е.
- корень уравнения (2.7), т.е.  , а
, а  и
и  непрерывна. Тогда существуют окрестность корня
непрерывна. Тогда существуют окрестность корня  такая, что если начальное приближение
такая, что если начальное приближение  принадлежит этой окрестности, то для метода Ньютона (2.8) последовательность значений
принадлежит этой окрестности, то для метода Ньютона (2.8) последовательность значений  сходится к
сходится к  при
при  .
.
Заметим, что точка  может являться как точкой минимума, так и точкой максимума, а может (при
может являться как точкой минимума, так и точкой максимума, а может (при  ) вообще не являться точкой экстремума. Если функция
) вообще не являться точкой экстремума. Если функция  имеет как минимумы, так и максимум то она может сходиться и к точкам минимума, и к точкам максимума в зависимости от того, из окрестности какой критической точки взято начальное приближение. При этом, в отличие от других методов оптимизации, формула для поиска максимума функции совпадает с формулой для поиска минимума.
имеет как минимумы, так и максимум то она может сходиться и к точкам минимума, и к точкам максимума в зависимости от того, из окрестности какой критической точки взято начальное приближение. При этом, в отличие от других методов оптимизации, формула для поиска максимума функции совпадает с формулой для поиска минимума.
Формулу метода Ньютона решения задачи оптимизации можно получить и из других соображений. Разложим функцию  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки  , ограничившись линейными и квадратичными членами относительно приращения
, ограничившись линейными и квадратичными членами относительно приращения  :
:

 (2.9)
(2.9)
В качестве следующего приближения  к оптимальному значению проектного параметра
к оптимальному значению проектного параметра  возьмем точку экстремума функции
возьмем точку экстремума функции  . Имеем
. Имеем

что совпадает с (2.8). Разложение (2.9) в окрестности точки  , на котором график функции
, на котором график функции  заменяется параболой графиком функции
заменяется параболой графиком функции  .
.
Относительно сходимости метода Ньютона решения задачи оптимизации можно сделать замечания. Метод Ньютона обладает более быстрой сходимостью по сравнению с методами, которые не используют дифференциальные свойства функции (например, с методом золотого сечения). Однако сходимость метода Ньютона не гарантирована, при неудачном выборе начального приближения он может расходиться.