Зачтенная работа предъявляется преподавателю на экзамене.

В случае затруднений в решении задач студенты могут обращаться за консультацией (письменной или устной) к преподавателю в институт.

 

Задача 1. Построить на плоскости область решений системы линейных неравенств и найти максимальное и минимальное значения линей­ной функции в этой области.

№ варианта  


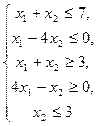
Задача 2. Для реализации трех групп товаров коммерческое предпри­ятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве единиц, ресурса второго вида в количестве единиц, ресурса третьего вида в количестве 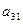единиц. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарообо­рота расходуется соответственно ресурса первого вида в количест­ве единиц, ресурсов второго вида в количестве 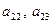единиц, ресурсов третьего вида в количестве 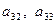единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота состав­ляет соответственно (тыс. руб.).

Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.

№ варианта  
а11=4, а12=8, а13=2, а21=3, а22=8, а23=4, а31=12, а32=4, а33=6, b1=116, b2=240, b3=432, с1=8, с2=6, с3=6.  

В задаче 2, необходимо:

- Составить математическую модель планирования товароборота;

- решить симплексным методом;

- составить двойственную задачу линейного программирования;

- установить сопряженные пары переменных прямой и двойственной задач;

- согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров

 

Задача 3. Графический метод и симплекс-метод. В таблице 2 приведены данные о предприятии, производящем продукцию двух типов Р1 и Р2 из сырья трех видов S1, S2, S3 . Запасы сырья равны соответственно b1, b2, b3. Расход i-го вида сырья на единицу j-го вида продукции равен aij. Доход, получаемый предприятием от реализации единицы j-го вида продукции, равен сj. Найти план производства, обеспечивающий предприятию максимум дохода. Решить задачу геометрическим способом и симплекс-методом. Найти оптимальное решение двойственной задачи, дать экономическую интерпретацию. Данные по вариантам приведены в таблице 3.

Таблица 2

bj P1 P2
b1 a11 a12
b2 a21 a22
b3 a31 a32
cj c1 c2

 

 

Таблица 3

Номер варианта Таблица

 

bj P1 P2
cj

 

 

Задача 4. Транспортная задача. На трех станциях отправления сосредоточен однородный груз (информация о запасах представлена матрицей А). Этот груз следует перевезти в пять пунктов назначения, имеющих потребности в этом грузе (информация о потребностях представлена матрицей В). Стоимость перевозок единицы груза от каждой станции до каждого пункта назначения считается известной и представлена матрицей С. Требуется составить такой план перевозок, при котором их общая стоимость окажется минимальной. Матрицы А, В, С представлены в таблице 4.

Таблица 4.

Номер варианта Матрица А Матрица В Матрица С
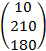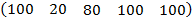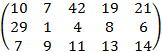