Мощность множества

Для конечных множеств, только которые и рассматриваются в нашем курсе, мощность множества совпадает с количеством его элементов. Мощность множества А обозначается М(А). Мощность множества тесно связана с классическим определением вероятности, которое будет изучаться в нашем курсе, поэтому мы остановимся на нем подробнее.

Имеют место равенства:

(1) М(Ø) = 0

(2) М(AÈB) = М(А) + М(В) - М(A Ç B)

(3) М(A \ B) = М(А) - М(A Ç B)

Следствия:

(с1) Если М(A Ç B) = 0, то М(AÈB) = М(А) + М(В)

(с2) Если М(A Ç B) = 0, то М(A \ B) = М(А)

(с3) Если М(В \ А) = 0, то М(A \ B) = М(А) - М(В)

 

ПРИМЕР 1

А = {2, 3, 4, 7}

B = {3, 4, 5}

A Ç B = {3, 4}

A È B = {2, 3, 4, 5, 7}

A \ B = {2,7}

М(А)=4

М(В)=3

М(A Ç B)=2

М(A È B)=3+4-2=5

(Если внимательно посмотреть на эти выкладки, мы увидим, что при суммировании М(А) + М(В) М(A Ç B) суммируется дважды, поэтому и нужно ее вычесть. В данном примере дважды суммируются элементы 3 и 4)

 

М(A \ B)=4-2=2

 

ПРИМЕР 2 (задача на применение этих формул).

Имеется 2 дополнительных курса: математика и физика.

В группе 30 учащихся и все из них занимаются на дополнительных курсах, 20 занимаются математикой, 15 занимаются физикой.

Сколько учащихся занимается только математикой?

РЕШЕНИЕ.

В данном случае U = вся группа. М(U) = 30.

А – множество учащихся, занимающихся математикой.

В - множество учащихся, занимающихся физикой.

М(AÈB) = М(U) = 30. Так как, по условию, нет учащихся, не занимающихся дополнительно.

Нам нужно найти М(A \ B). Нужно применить формулу (3). Найдем М(A Ç B) из формулы (2).

М(A Ç B) = М(А) + М(В) - М(AÈB)= 35-30=5.

Тогда М(A \ B) = М(А) - М(A Ç B)=20-5=15.

Наглядно решение этой задачи можно представить такой диаграммой.

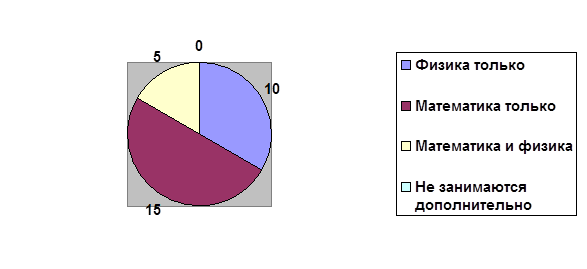
Сравним ее с диаграммой исходного условия

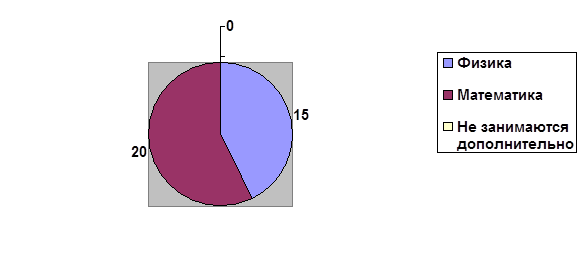
Очевидно, первая диаграмма гораздо больше и нагляднее освещает для нас суть ситуации.

Эта несложная задача показывает, как теория множеств может помочь педагогу выявить скрытые параметры ситуации, сложившейся в учебном процессе, и представить их наглядно. Может возникнуть впечатление, что такие задачи можно решать «в лоб» на основе обычной школьной арифметики. Это впечатление ложно. Чтобы в этом убедиться, достаточно попробовать решить эту же задачу для 3 учебных предметов.