Задача № 1.

1.1. Пусть А В. Упростить выражения А В, А+В, А В С, А+В+С.

1.2. Бросаются две игральные кости. Пусть А- событие, состоящее в том, что сумма очков нечетная, В - событие, состоящее в том, что хотя бы на одной из костей выпала единица. Описать события .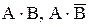

1.3. Дана система S, состоящая из блоков 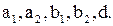Записать событие S, состоящее в том, что система S исправна.

 
 


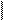
a1 a2 b1 b2

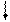d

 

1.4. Пусть А,В,С - три произвольных события. Найти выражения, если:

- произошло только событие А;

- произошло одно и только одно событие;

- произошло два и только два события;

- все три события произошли;

- произошло не более двух событий.

1.5. Пусть событие А - падает снег, событие В - идет дождь. Выразить через

А и Вследующие события: а) дождь со снегом; б) дождь или снег; в) нет дождя;

г) ясная погода; д) падает снег без дождя.

1.6. Бросаются две игральные кости: одна черная, а другая белая. Отмечается число очков, выпавших на каждой кости. Сколько элементарных событий соответствует тому, что а) сумма очков больше 10? б) сумма очков - четная?

1.7. Машинно-котельная установка состоит из двух котлов и одной машины. Событие А - исправна машина, событие Вк( к = 1,2) - исправен k-й котел. Событие Созначает работоспособность машинно-котельной установки, что будет в том случае, если исправна машина и хотя бы один котел. Выразить события С и 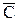через А и Вк .

1.8. Образуют ли полную группу следующие наборы событий (дать полный ответ, доказать). Опыт:

а) Бросание двух монет; события: А 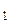- появление двух гербов, А 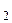- появление двух цифр.

б) Два выстрела по мишени; события: 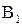- хотя бы попадание, В 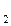- хотя бы один промах.

1.9. Образуют ли полную группу следующие группы событий (дать полный ответ, доказать). Опыт:

а) Бросание игральной кости; события: А1- появление не менее трех очков, А2- появление не более четырех очков.

б) Два выстрела по мишени; cобытия: В1 - ни одного попадания, В2 - одно попадание,В3 - два попадания?

1.10. Производится наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события:

А - обнаружен ровно один из четырех объектов,

В - обнаружен хотя бы один объект. Указать (с доказательством), в чем состоят события А + В; А В.

1.11. Каковы соотношения между событиями А,В и С, если АВС=А; если А+В+С=А? Дать геометрическую интерпретацию.

1.12. Назвать противоположные события для следующих событий: С - три по-падания при трех выстрелах; Д - хотя бы одно попадание при пяти выстрелах.

1.13. Назвать противоположные события для следующих событий: А - не более двух попаданий при пяти выстрелах, В - выигрыш первого игрока при игре в шахматы.

1.14. Событие В есть частный случай события А, т.е. из появления события В следует, что событие А произошло. Следует ли из 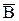, что 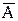произошло? Следует ли из 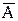событие ?

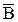1.15. Мишень состоит из десяти кругов, ограниченных концентрическими окру-жностями с радиусами 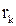(к=1,2,...,10), причем r2< r2< ...< r10. Событие Аk – попа-дание в круг радиусом rk. Что означают события 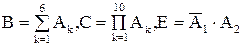. Что представляет собой событие ?

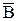1.16. События А - хотяо он играет на гитаре, а событие С - в том, что он живет в общежитии. Описать событие АВС. При каком условии будет иметь место тождество АВС=А? Когда будет равенство А=В? Будет ли оно иметь место, если все юноши играют на гитаре?

1.27. Производится наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события: В - обнаружен хотя бы один объект; С -обнаружено не менее двух объектов, D - обнаружено ровно два объекта; Е -обнаружено ровно три объекта, F - обнаружены все четыре объекта. Указать, в чем состоят события D+Е+F, ВС.

1.28. Событие А - хотя бы одно из имеющихся четырех изделий бракованное, событие В - бракованных изделий среди них не менее двух. Что означают противоположные события и ?

1.29. Опыт - передача (в одинаковых условиях) трех сообщений равной длины. Рассматривая события: А - искажено первое сообщение; В - искажено второе сообщение; С - искажено третье сообщение. Ответить на следующие вопросы: образуют ли они полную группу, являются ли несовместными, являются ли равновозможными?

1.30. Опыт – Брошены 2 игральные кости. Образуют ли полную группу событий следующие наборы: А - на обеих костях шестерки, В - ни на одной кости нет шестерки, С - на одной из костей шестерка, на другой – нет. (Указать, образуют ли они в данном опыте полную группу событий).