Алгебра событий .

Событие называется невозможным, если оно в эксперименте заведомо не наступит и обозначается 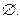Событие называется достоверным, если оно в эксперименте заведомо наступит и обозначается 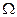. Само множество 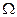является достоверным событием, поскольку один из его исходов обязательно произойдет. Так , в примере 2 событие – « выпадение числа очков, равного 7», является в данном случае невозможным , а событие – «выпадение числа очков, не более 6», – достоверное событие.

Если в случайном эксперименте из наступления события А следует наступление события В, то говорят , что А влечет В ( А В ).

Если А В , а В А. то говорят ,что события А и В равносильны ( А = В ).

Суммой двух событий А и В называют событие А + В (А 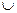В), происходящее тогда и только тогда, когда происходит или событие А , или событие В. Сумма событий соответствует объединению множеств , Рис.3.

 

 

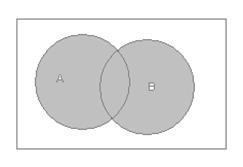
Рис.3

В примере 2 А + В= { 2, 4, 5, 6}.

Аналогичный смысл имеет сумма любого числа событий. Если I-произвольное множество значений некоторого индекса i, A 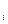-некоторое множество событий то сумма есть событие ,происходящее тогда и только тогда, когда происходит хотя бы одно событие.

Произведением двух событий А и B называют событие AВ (А 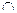В), происхо-

дящее тогда и только тогда, когда происходит и событие А, и событие В ( все события А , i ) .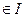

Произведение событий соответствует пересечению множеств, (Рис.4).

 

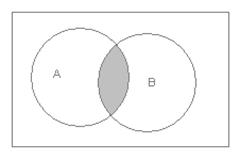
Рис.4

Для событий из примера 2 АВ = { 4, 6 }.

Разностью А \ В двух событий А и В есть событие, происходящее тогда и только тогда. когда происходит А , но не происходит В. Разность событий соответствует разности множеств, (Рис.5)

 

Рис.5.

В примере 2 А \ В = {2}.

Событие называется противоположным событию А, если оно происходит тогда и только тогда, когда не происходит А (соответствует дополнению множеств) Рис. 6.

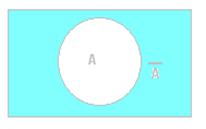
Рис.6.

В примере 2 = { 1, 3, 5 }.

Операции сложения и умножения событий обладают следующими свойствами :

а) А+В = В+А , АВ = ВА (коммутативность);

б) (А+В)+С=А+(В+С) , А(ВС)=(АВ)С (ассоциативность);

в) (А+В)С=АС+ВС) (дистрибутивность умножения относительно cложения).

Отметим еще некоторые очевидные соотношения:

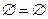А , А , , .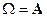

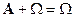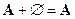Два события А и В называются несовместными, если невозможно их совместное наступление, иными словами АВ = 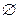.Примером несовместных событий являются А и .

Совокупность событий 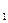А ,А 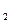, … , А 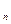составляет полную группу попарно несовместных событий , если:

1) хотя бы одно из этих событий непременно происходит;

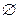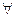2) любая пара событий несовместна , А А = , i 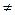j, i,j= .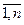