Две бесконечно малые величины называются эквивалентными, если предел их отношения равен единице.
! Пример: x, sinx и tgx являются эквивалентными x ® 0.
Из свойства эквивалентности вытекает следующее правило при раскрытии неопределенностей. Под пределом одну эквивалентную величину можно заменить другой эквивалентной величиной.
Например, sinx и tgx можно заменить на x, sin2x и tg2x - на 2x, ln(1 + 3x) - на 3x и т.д x ® 0.
Если отношение a/b двух бесконечно малых величин само бесконечно мало, то  называется величиной высшего порядка малости относительно b.
называется величиной высшего порядка малости относительно b.
! Пример: x² является бесконечно малой высшего порядка малости относительно бесконечно малой x при x ® 0.
Если y – бесконечно большая величина, то 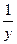 – бесконечно малая и наоборот.
– бесконечно малая и наоборот.
@ Задача 7. Найти предел функции 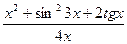 при x ® 0.
при x ® 0.
Решение: Предел находится применением свойств бесконечно малых величин:
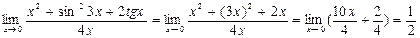 .
.