Примеры расчета переходных процессов в электрических цепях

 

Задача 4.2.1 В электрической цепи (см. рисунок 4.1), с параметрами:

, ,

до коммутации был установившийся режим, создаваемый источником постоянной ЭДС . В момент ключи одновременно замыкаются.

Требуется определить: ток в ветви с ЭДС и построить его график.

Рисунок 4.1 – Схема электрической цепи

 

Решение.

Классический метод расчета переходного процесса.

Определим независимые начальные условия (ННУ) .

Рассчитаем установившийся режим в цепи до коммутации.

,

,

(4.1)

Запишем дифференциальные уравнения по законам Кирхгофа для цепи после коммутации:

 

(4.2)

 

Ток i₁(t) представим в виде суммы принужденного и свободного токов:

.

Определим принуждённый ток . Рассчитаем установившийся режим в цепи после коммутации.

 

. (4.3)

 

 

Определим свободный ток .

Получим характеристическое уравнение методом входного сопротивления:

 

Приравняем к нулю числитель:

. (4.4)

Подставим в уравнение (4.4) числовые значения:

.

Определим корни характеристического уравнения:

, .

Корни характеристического уравнения вещественные и различные. Свободный ток запишем в виде:

. (4.5)

Для определения постоянных интегрирования А_1, А₂ запишем ток i₁ и определим его производную:

. (4.6)

.

Определим постоянные интегрирования А_1, А₂ по начальным значениям i₁(0), i^/₁(0):

(4.7)

Найдём i₁(0), i^/₁(0) из законов Кирхгофа, записанных для цепи после коммутации (4.2):

;

;

. (4.8)

Рассчитаем i₁(0):

.

Продифференцируем выражение (4.8) и определим i^/₁:

. (4.9)

Запишем это уравнение для момента времени t=0:

.

Из законов Кирхгофа, записанных для момента времени t=0, найдём i_L^/(0), u_c^/(0) и определим i^/₁(0):

;

;

.

Подставим найденные числовые значения i₁(0), i^/₁(0) в систему (4.7) и определим постоянные интегрирования:

;

А₁ = − 0,348, А₂ = 0,089.

Подставим найденные значения А₁= – 0,348, А₂= 0,089 в выражение (4.6) и получим переходный ток :

.

Операторный метод расчета переходного процесса.

Независимые начальные условия определены в классическом методе и равны:

Нарисуем эквивалентную операторную схему для цепи после коммутации.

Рисунок 4.2 – Эквивалентная операторная схема

 

Определим изображение тока методом контурных токов:

(4.10)

Решим систему уравнений (4.10), определим :

,

.

, (4.11)

где

 

Определим корни характеристического уравнения

,

.

Таким образом, корни знаменателя изображения тока равны:

p = 0, .

Ток i₁(t) запишем по теореме разложения в виде:

. (4.12)

Рассчитаем:

;

Подставим рассчитанные значения в теорему разложения (4,12), получим переходный ток:

.

На рисунке 4.3 показаны графики принужденного тока , свободного тока и переходного тока .

 

 

Рисунок 4.3 – График тока

 

Задача 4.2.2. В электрической цепи (см. рисунок 4.4) с постоянным источником ЭДС Е = 60В в момент времени t = 0 одновременно ключ К₁ замыкается, а ключ K₂ размыкается. Параметры цепи: резисторы R₁=30 Ом, R₂=70Ом, R₃=30 Ом, индуктивность L = 10 мГн, емкость C = 2 мкФ.

Требуется:

1) определить ток i_L(t) после коммутации;

2) построить график тока i_L(t).

 

 

Рисунок 4.4 – Схема электрической цепи

 

 

Решение.

Классический метод расчета переходного процесса.

Определим независимые начальные условия (ННУ): i_L(0), u_C(0). Рассчитаем установившийся режим в цепи до коммутации.

Рисунок 4.5 – Схема электрической цепи до коммутации

 

(4.13)

По законам коммутации:

(4.14)

Запишем дифференциальные уравнения по законам Кирхгофа для цепи после коммутации. Сначала упростим схему:

 

Схема цепи после коммутации представлена на рисунке 4.6.

Рисунок 4.6 – Схема электрической цепи после коммутации

Дифференциальные уравнения по законам Кирхгофа для цепи после коммутации запишем в виде:

(4.15)

Ток i_L(t) представим в виде суммы составляющих принужденного и свободного токов:

i_L(t) = i_Lпр(t) + i_Lсв(t).

Определим составляющую принуждённого тока i_Lпр(t). Рассчитаем установившийся режим в цепи после коммутации.

 

(4.16)

 

Определим составляющую свободного тока i_Lсв(t).

Получим характеристическое уравнение методом входного сопротивления:

.

Приравняем к нулю числитель, подставим числовые значения и определим корни характеристического уравнения:

(4.17)

Корни характеристического уравнения комплексно-сопряженные. Составляющую свободного тока запишем в виде:

.

Запишем переходный ток

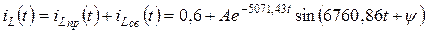(4.18)

Для определения постоянных интегрирования А и ψ возьмем производную по времени t от тока i_L(t):

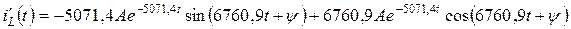. (4.19)

Запишем выражения (4.18) и (4.19) для момента времени t = 0:

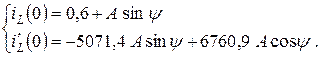(4.20)

Значение производной 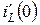найдем из второго уравнения системы (4.15), записанного для момента времени t = 0:

.

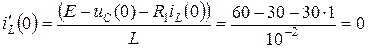Подставим значения i_L(0)=1А и 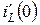= 0 в систему уравнений (4.20), получим:

(4.21)

Подставим 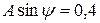во второе уравнение системы (4.21):

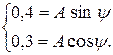(4.22)

Поделим первое уравнение системы (4.22) на второе, получим:

, ;

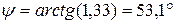постоянную интегрирования А определим по формуле:

.

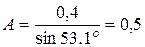Подставим найденные значения в выражение (4.18) и получим переходный ток i_L(t):

.

 

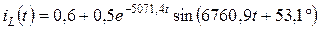Операторный метод расчета переходного процесса.

Независимые начальные условия определены в классическом методе и равны: .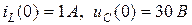

Нарисуем эквивалентную операторную схему для цепи после коммутации.

 

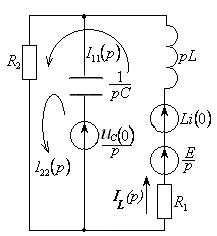
Рисунок 4.7 – Эквивалентная операторная схема

Определим изображение тока I_L(p) методом контурных токов:

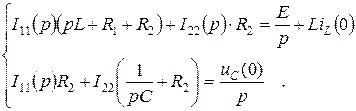(4.23)

Решим систему уравнений (4.23) и найдем :

 

 

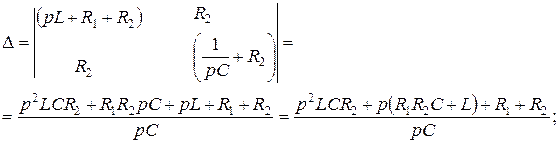
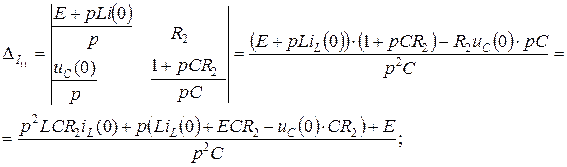
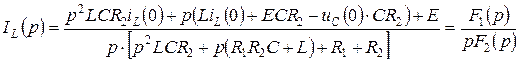, (4.24)

где

.

Определим корни характеристического уравнения

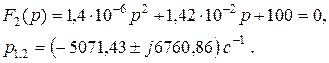
Таким образом, корни знаменателя тока I_L(p) равны:

, .

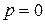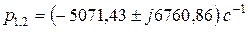Ток i_L(t) запишем по теореме разложения в виде:

. (4.25)

Рассчитаем:

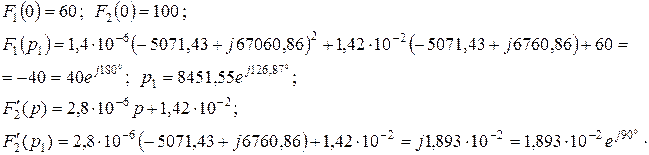
Подставим рассчитанные значения в выражение теоремы разложения (4.25), получим переходный ток i_L(t):

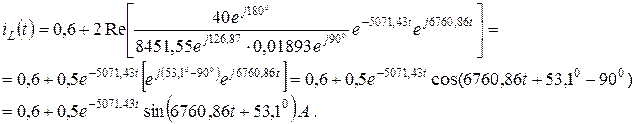
На рисунке 4.8 показаны графики составляющих принужденного i_Lпр(t) и свободного i_Lсв(t) токов, а также переходного тока i_L(t).

 

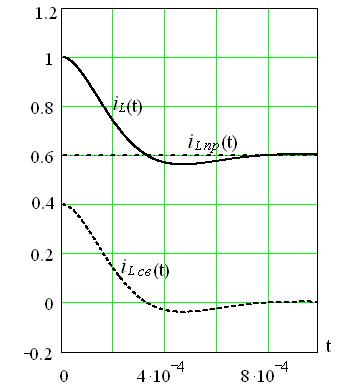
Рисунок 4.8 – Графики тока i_L(t) и его составляющих

 

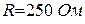Задача 4.2.3. В электрической цепи (см. рисунок 4.9) в момент времени ключ К переключается с полюса 3 на полюс 1. Параметры цепи: постоянный источник ЭДС , сопротивления , индуктивность 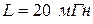, конденсатор емкостью .

Требуется: определить: напряжение на емкости u_C (t) после коммутации; построить график напряжения на емкости u_C(t); определить токи во всех ветвях цепи после коммутации.

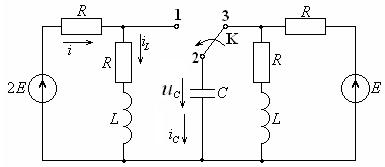
Рисунок 4.9 – Схема электрической цепи

 

Решение.

Классический метод расчета переходного процесса.

Определим независимые начальные условия (ННУ): 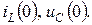Рассчитаем установившийся режим в цепи до коммутации.

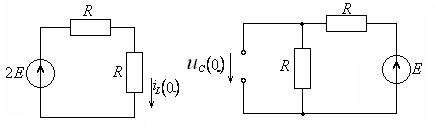
Рисунок 4.10 – Схемы для расчета ННУ

 

(4.26)

Уравнения по законам Кирхгофа для цепи после коммутации запишем в виде:

(4.27)

Переходное напряжение u_C(t) запишем в виде

.

Определим путем расчета установившегося режима в цепи после коммутации.

 

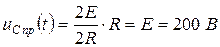. (4.28)

 

 

Определим свободную составляющую напряжения на ёмкости .

Составим характеристическое уравнение методом входного сопротивления:

.

Приравняем к нулю числитель и получим характеристическое уравнение в виде:

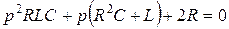. (4.29)

Подставим числовые значения и определим корни характеристического уравнения: ; .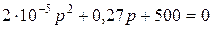

Корни характеристического уравнения вещественные и различные. Свободную составляющую напряжения запишем в виде:

.

Для определения постоянных интегрирования А₁, А₂ запишем напряжение u_C(t) и определим его производную :

; (4.30)

.

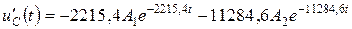Постоянные интегрирования А_1, А₂ определим по начальным значениям u_C(0), :

(4.31)

Начальное значение u_C(0)=100В. Производная . Найдем i_C(0) из первого и третьего уравнений, записанных по законам Кирхгофа для цепи после коммутации в начальный момент времени t = 0 (4.27):

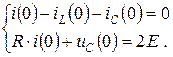(4.32)

Из второго уравнения определим i(0), подставим в первое уравнение и найдем ток i_C(0), а затем :

;

;

.

Подставим u_C(0)=100В и в систему уравнений (4.31) и определим постоянные интегрирования А₁ и А₂:

.

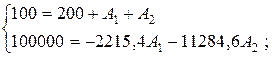
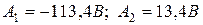Подставим найденные значения А₁, А₂ в выражение (4.30) и получим переходное напряжение на конденсаторе u_C(t):

.

Определение токов во всех ветвях цепи после коммутации по найденному значению u_C(t):

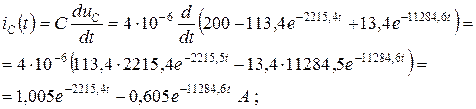
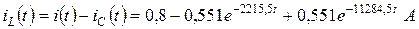. (4.33)

Операторный метод расчета переходного процесса.

Независимые начальные условия определены в классическом методе и равны: .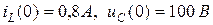

Нарисуем эквивалентную операторную схему для цепи после коммутации.

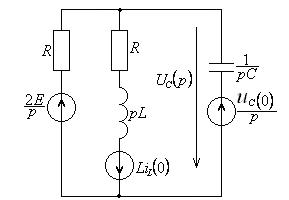
Рисунок 4.11 – Эквивалентная операторная схема

Изображение напряжения на конденсаторе найдем методом двух узлов:

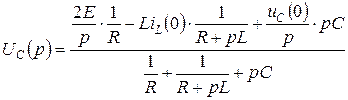. (4.34)

Преобразуем выражение (4.34), получим:

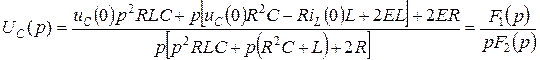. (4.35)

Подставим числовые значения в выражение для изображения напряжения:

,

где

, .

Определим корни характеристического уравнения .

.

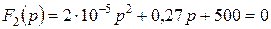Корни уравнения равны:

.

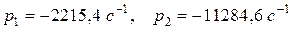Таким образом, корни знаменателя изображения напряжения U_C (p) равны: , .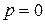

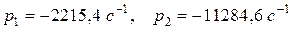Так как знаменатель имеет нулевой корень и корни характеристического уравнения вещественные и различные, u_C(t) запишем по теореме разложения в виде:

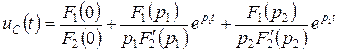. (4.36)

Определим выражение производной 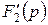и рассчитаем для p₁ и p₂:

Рассчитаем остальные компоненты выражения (4.36):

;

.

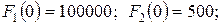
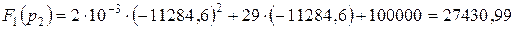Подставим рассчитанные значения в выражение (4.36) и получим напряжение на конденсаторе u_C(t):

.

Рисунок 4.12 – Графики принужденного и свободного переходного напряжения u_C(t)

 

Задача 4.2.4. В электрической цепи (см. рисунок 4.13) с источниками постоянной ЭДС: Е₁=100В и Е₂=50В, сопротивлениями: R₁ = R₃ = 40Ом, R₂ = =R₄ = 60Ом, R₅ = R₆ = 20Ом, индуктивностью L = 20 мГн, емкостью С = 2 мкФ: в момент времени t = 0 ключ К размыкается и в цепи происходит переходный процесс.

Определить: ток , напряжение 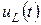после коммутации и построить графики и .

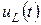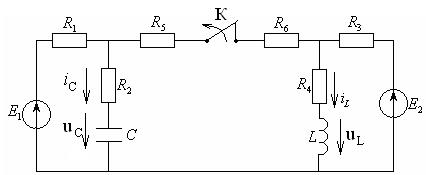
Рисунок 4.13 – Схема электрической цепи

 

Решение.

Переходный процесс в цепи рассчитаем классическим методом.

Определим независимые начальные условия: .

Независимые начальные условия определяются путем расчета установившегося режима в цепи до коммутации (см. рисунок 4.14).

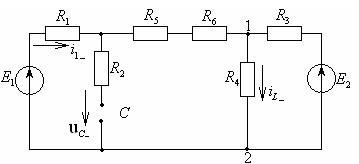
Рисунок 4.14 – Схема электрической цепи до коммутации

 

Найдем напряжение u₁₂(0 –) по методу двух узлов:

.

Токи рассчитаем по закону Ома:

.

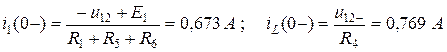Напряжение на конденсаторе в цепи до коммутации равно:

.

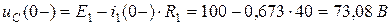По законам коммутации:

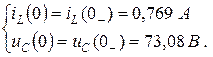(4.37)

После размыкания ключа заданная электрическая цепь распадается на две независимые цепи первого порядка (см. рисунки 4.15 а и 4.15 б).

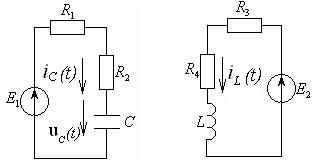
а) б)

Рисунок 4.15 – Электрические цепи после коммутации

 

Для нахождения емкостного тока i_С(t) рассчитаем переходный процесс в цепи (см. рисунок 4.15 а). Так как ток в емкости равен 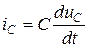, рассчитаем переходное напряжение на емкости u_C(t). Переходное напряжение на емкости представим в виде: u_C(t) = u_Cпр(t)+u_Cсв(t).

Определим принужденное напряжение на емкости u_Cпр(t), путем расчета установившегося режима в цепи после коммутации (см. рисунок 4.16 а).

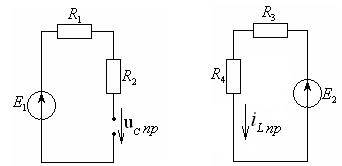
а) б)

Рисунок 4.16 – Эквивалентные схемы для расчета установившихся режимов после коммутации

 

Как видно из рисунка 4.16 а, .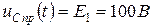

Определим свободное напряжение на емкости u_Cсв. Характеристическое уравнение получим методом входного сопротивления. Входное сопротивление цепи (см. рисунок 4.15 а) имеет вид:

. (4.38)

Приравняем Z(p) к нулю и определим корень характеристического уравнения Z(p) = 0:

; .

Свободную составляющую u_Cсв(t) и результирующее переходное u_C(t) напряжения на емкости запишем в виде:

, .

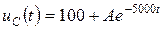Найдем постоянную интегрирования А по начальному значению напряжения u_C(0)=73,1 В:

73,1 = 100+А, отсюда определим А=73,1 – 100 = – 26,9 В.

Переходное напряжение на ёмкости равно:

.

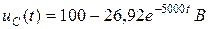Определим ток в цепи:

. (4.39)

Как видно из выражения (4.39), принужденный ток в емкости равен нулю и .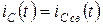

График тока приведен на рисунке 4.17.

Рисунок 4.17 – График переходного тока i_C(t)

 

Для нахождения напряжения на индуктивности u_L(t) рассчитаем переходный процесс в цепи (см. рисунок 4.15 б). Так как напряжение на индуктивности u_L(t) равно , рассчитаем ток в индуктивности i_L(t). Ток в индуктивности представим в виде: i_L(t) = i_Lпр(t)+ i_Lсв(t).

Определим принужденный ток в индуктивности i_Lпр(t), путем расчета установившегося режима в цепи после коммутации (см. рисунок 4.16 б).

Принуждённый ток в индуктивности равен:

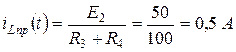. (4.40)

Определим свободную составляющую тока в индуктивности i_Lсв(t), для этого составим характеристическое уравнение методом входного сопротивления. Входное сопротивление цепи (см. рисунок 4.15 б) имеет вид:

.

Приравняем Z(p) к нулю и определим корень характеристического уравнения:

, откуда получим .

Свободную составляющую тока i_Lсв(t) и результирующий переходный ток в индуктивности i_L(t) запишем в виде:

. (4.41)

Найдем постоянную интегрирования А по независимому начальному значению тока в индуктивности i_L(0 –)=0,769А из уравнения составленного на основании закона коммутации :

0,5+А = 0,769, отсюда определим А = 0,769 – 0,5 =0,269А.

Переходный ток в индуктивности равен: .

Напряжение на индуктивности определим по формуле:

. (4.42)

Как видно из выражения (4.42), принуждённая составляющая напряжения на индуктивности равна нулю и результирующее напряжение состоит только лишь из свободной составляющей u_L(t) = u_Lсв(t).

График напряжения на индуктивности u_L(t) приведен на рисунке 4.18.

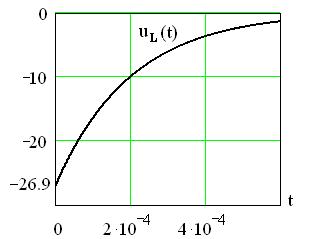
Рисунок 4.18 – График переходного напряжения u_L(t)

 

Задача 4.2.5 Электрическая цепь (см. рисунок 4.19) содержит два источника с одинаковыми постоянными ЭДС Е = 100В, сопротивления и , индуктивности и 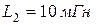, ёмкост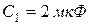и и . В момент времени ключи К₁ и К₂ одновременно размыкаются.

Требуется:

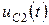1) определить напряжения на конденсаторах и после размыкания ключей;

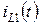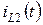2) определить токи в индуктивностях и после размыкания ключей;

3) построить графики , , , .

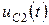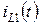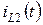Решение.

Переходный процесс в цепи рассчитаем классическим методом.

Определим независимые начальные условия:

и .

Независимые начальные условия определим путем расчета установившегося режима в цепи до коммутации (см. рисунок 4.20). Как видно из рисунка 4.20, независимые начальные условия равны:

, ,

, .

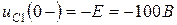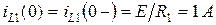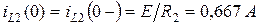Рисунок 4.19 – Схема электрической цепи

 

Рисунок 4.20 – Эквивалентная схема для расчета установившегося режима в цепи до коммутации

 

Схема электрической цепи после коммутации показана на рисунке 4.21.

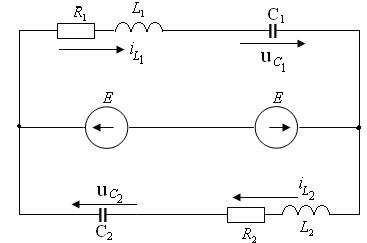
Рисунок 4.21 – Схема электрической цепи после коммутации

Напряжение между узлами электрической цепи (см. рисунок 4.21) равно нулю (Е − Е = 0), и электрическая цепь после коммутации распадается на две независимые цепи (см. рисунки 4.22 а и 4.22 б).

а) б)

Рисунок 4.22 – Схемы для расчета , , ,

 

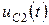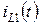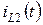
Рассчитаем переходной процесс в R₁L₁C₁ – цепи (см. рисунок 4.22 а) и определим и .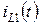

Найдем сначала переходное напряжение : .

Принуждённая составляющая напряжения и переходное напряжение состоит только из свободной составляющей: . Для определения свободной составляющей напряжения составим характеристическое уравнение методом входного сопротивления и найдем его корни.

Входное комплексное сопротивление цепи, где jω заменено оператором p, приведем к общему знаменателю и приравняем к нулю числитель, получим:

. (4.43)

Корни характеристического уравнения (4.43) равны:

.

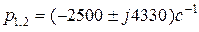Корни характеристического уравнения комплексно-сопряженные, свободное напряжение запишем в виде:

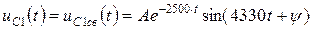. (4.44)

Постоянные интегрирования А и ψ определим по начальным значениям напряжения и его первой производной 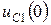, 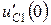. Производная имеет вид:

.

Запишем 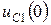и :

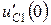(4.45)

Начальное значение напряжения 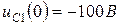, так как , то 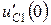равно: .

Подставим найденные значения 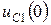, 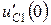в систему уравнений (4.45), получим:

(4.46)

Решая систему уравнений (4.46), найдем постоянные интегрирования А и ψ:

 

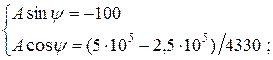
(4.47)

 

;

.

Подставим найденные значения постоянных интегрирования в выражение (4.44) и получим переходное напряжение на конденсаторе:

.

Ток в цепи определим по формуле:

. (4.48)

Чтобы сложить синусоидальные функции времени, применим комплексный метод расчета:

;

;

.

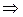
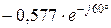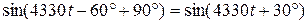
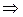
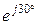Перейдем к мгновенным значениям:

.

Таким образом, сумма двух синусоидальных функций равна:

. (4.49)

Подставим (4.49) в формулу (4.48) и получим выражение для тока :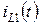

. (4.50)

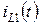Графики напряжения тока представлены на рисунках 4.23 а и 4.23 б.

а) б)

Рисунок 4.23 – Графики напряжения и тока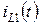

 

Рассчитаем переходной процесс в R₂L₂C₂ – цепи (см. рисунок 4.22 б) и определим , .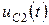

Найдем сначала переходное напряжение :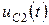

.

Принуждённая составляющая напряжения и переходное напряжение включает только свободную составляющую: .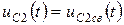

Для определения свободной составляющей напряжения составим характеристическое уравнение методом входного сопротивления и найдем его корни. Комплексное сопротивление цепи (jω → p) приведем к общему знаменателю, приравняем к нулю числитель, получим:

. (4.51)

Корни характеристического уравнения (4.51) равны:

.

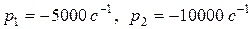Корни характеристического уравнения вещественные и различные, напряжение на емкости запишем в виде:

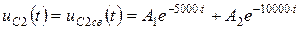. (4.52)

Постоянные интегрирования определим по начальным значениям напряжения и его первой производной 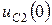, . Производная имеет вид: .

Запишем 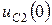и :

(4.53)

Начальное значение напряжения 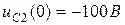, так как , то равно .

Подставим найденные значения 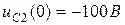и в систему уравнений (4.53), получим:

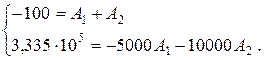(4.54)

Решая систему уравнений (4.54), найдем постоянные интегрирования А₁ и А₂: А₁ = −133,3 и А₂ = 33,3.

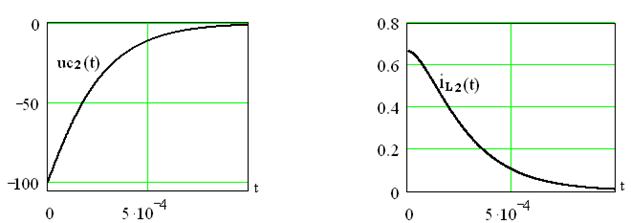
Подставим найденные значения постоянных интегрирования в выражение (4.52) и получим переходное напряжение на емкости:

.

Ток в цепи 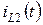определим по формуле:

.

Графики напряжения и тока 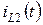представлены на рисунках 4.24 а и 4.24 б.

а) б)

Рисунок 4.24 – Графики напряжения и тока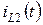

 

Список литературы

 

1. Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. – 544 с.

2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высшая школа,1981. – 333 с.

3. Основы теории цепей. Учебник для вузов/Г.В.Зевеке и др. – М.: Энергоиздат, 1989. – 528 с.

4. Теория линейных электрических цепей/Под редакцией И.Г.Кляцкина. – М.: Высшая школа, 1975.

5. Зернов И.В., Карпов В.Г. Теория радиотехнических цепей. – Л.: Энергия, 1972.

6. Шебес М.Р., Каблукова М.В. Задачник теории линейных электрических цепей: Учебное пособие для вузов. – М.: ВШ, 1990.-544 с.

7. Основы теории цепей: Учебник для вузов/В.П.Бакалов и др. – М.: 2000. – 592 с.

8. Попов В.П. Основы теории цепей: Учебник для вузов. – М., 2000. –576с.

9. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. – т.1. – Санкт-Петербург: Питер, 2003. – 463 с.

10. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. – т.2. – Санкт-Петербург: Питер, 2003. – 576 с.

11. Жолдыбаева З.И., Зуслина Е.Х. Теория электрических цепей 1. Примеры расчета установившихся процессов в линейных электрических цепях. Учебное пособие. – Алматы: АИЭС, 2009.- 93 с.

12. Жолдыбаева З.И., Зуслина Е.Х. Теория электрических цепей 2. Примеры расчета установившихся и переходных процессов в линейных электрических цепях с сосредоточенными и распределенными параметрами. Учебное пособие. – Алматы: АИЭС, 2011. – 78 с.