Примеры решения задач.

1. Перечислить и указать на координатной плоскости все элементы декартова произведения множеств А={-2, 1, 3} и В={-1, 0, 2, 5}.

Решение: А×В={(-2,-1), (-2,0), (-2,2), (-2,5), (1,-1), (1,0), (1,2), (1,5), (3,-1), (3,0), (3,2), (3,5)}.

Заметим, что точки на координатной плоскости, изображающие элементы декартова произведения В×А, будут симметричны соответствующим точкам из А×В относительно биссектрисы первого и третьего координатных углов. ♦

2. Выяснить, какими свойствами обладает бинарное отношение η - «отношение больше» на множестве N.

Решение: Для любых натуральных чисел хηу, если х>у.

1) х>х – неверно для всех х 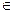Ν, т.е. данное отношение не является

рефлексивным;

2) для всякой пары натуральных чисел из х>у не следует у>х, т.е.

БО не является симметричным;

3) для любых х,у 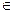Ν выполняется одно из неравенств: х>у или у>х,

т.е. отношение антисимметрично;

4) если х>у, а у>z, то справедливо х>z, т.е. БО транзитивно.