Границы числовых множеств
Пусть имеем числовое множество А.
Определение.Множество А называется ограниченным сверху, если существует такое число 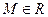 , что
, что 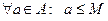 . Число
. Число 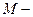 верхняя грань множества А. Очевидно, что если
верхняя грань множества А. Очевидно, что если 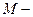 верхняя грань, то любое число
верхняя грань, то любое число  также является верхней гранью. Наименьшая из верхних граней – точная верхняя грань, которая обозначается:
также является верхней гранью. Наименьшая из верхних граней – точная верхняя грань, которая обозначается: 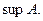
Определение.Множество А называется неограниченным сверху, если  существует
существует 
Определение.Множество А называется ограниченным снизу, если существует такое число  , что
, что  . Число
. Число  нижняя грань множества А. Очевидно, что если
нижняя грань множества А. Очевидно, что если  нижняя грань, то любое число
нижняя грань, то любое число 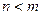 также является нижней гранью. Наибольшая из нижних граней – точная нижняя грань, которая обозначается:
также является нижней гранью. Наибольшая из нижних граней – точная нижняя грань, которая обозначается: 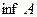
Определение.Множество А неограниченно снизу, если
для  существует
существует 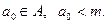
Определение.Множество А называется ограниченным, если оно ограничено и сверху и снизу.
Возникает вопрос: всегда ли для ограниченных множеств существуют 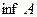 и
и 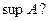 На этот вопрос отвечает следующая теорема:
На этот вопрос отвечает следующая теорема:
Теорема Дедекинда. Любое ограниченное сверху числовое множество имеет точную верхнюю грань, т.е. существует наименьший элемент среди верхних граней; и любое ограниченное снизу числовое множество имеет точную нижнюю грань, т.е. существует наибольший элемент среди нижних граней.
Например: для множества 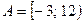 существуют
существуют  и
и 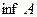 , также существует
, также существует  , который совпадает
, который совпадает 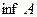 (
(  ), но не существует
), но не существует  .
.
Если в множестве А существует максимальный элемент, то 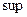 совпадает с максимумом. Если в множестве А существует минимальный элемент, то
совпадает с максимумом. Если в множестве А существует минимальный элемент, то 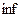 совпадает с минимумом.
совпадает с минимумом.
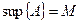
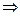 1)
1) 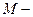 верхняя грань,
верхняя грань, 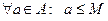 ;
;
2) 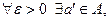 что
что 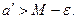

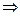 1)
1)  нижняя грань,
нижняя грань,  ;
;
2)  что
что 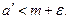
Утверждения 1) свидетельствуют о том, что 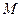 и
и 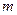 являются одной из верхних и нижних граней.
являются одной из верхних и нижних граней.
Утверждения 2) свидетельствуют о том, что эта грань является наименьшей и наибольшей соответственно и уменьшена (увеличена) соответственно быть не может.