Найти плотность тела и погрешность определения плотности.
Результаты прямых измерений массы m и объема V тела занесены в строку «среднее» табл. 1:
mср = 63,303 г; Δmср = 0,142 г;
Vср = 8,0457 см3; ΔVср = 0,0422 см3
Требуется:
а) записать результаты прямых измерений в стандартном виде в единицах СИ:
б) найти плотность тела и погрешность определения плотности:
в) пользуясь справочной таблицей плотностей определить материал тела.
а) mср ≈ 63,30 г = 63,30 ·10-3 кг ;
(сохранены две верные цифры 6 и 3, не имеющие погрешности, и две сомнительные цифры 3 и 0, содержащие погрешность);
Δmср ≈ 0,14 г = 0,14 ·10-3 кг ;
(округление до двух значащих цифр, т.к. первая из них – единица);
δm = Δmср / mср = 0,221 ·10-2 ;
Vср ≈ 8,05 см3 = 8,05 ·10-6 м3 ,
(сохранены две верные цифры 8 и 0 и одна сомнительная 5);
ΔVср ≈ 0,04 см3 = 0,04 ·10-6 м3 (округление до одной значащей ицифры);
δV = ΔVср / Vср = 0,50 ·10-2 ;
m = (63,30 ± 0,14) ·10-3 кг , δm = 0,221 % ;
V = (8,05 ± 0,04) ·10-6 м3 , δV = 0,50 % .
б) Среднее значение плотности:
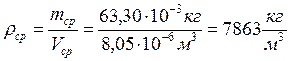
Относительная погрешность в определении плотности тела:
1) 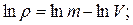 2)
2)  3)
3) 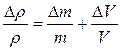
4) 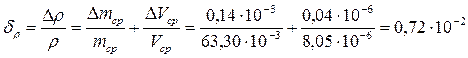 ;
;
Абсолютная погрешность Δρср :
Δρср = δρ ·ρср = 0,72·10-2 ·7,86·103 = 60 кг/м3
(Округление до одной значащей цифры)
Запись в стандартном виде:
ρ = (7,86 ± 0,06)·103 кг/м3 ; δρ = 0,72 %
(Сохранены две верные цифры 7 и 8 и одна сомнительная – 6)
в) В справочной таблице ближайшей к полученному значению является плотность железа:
ρтабл = 7800 кг/м3 = 7,8·103 кг/м3
Δρтабл = 100/2 = 50 кг/м3 (половина последнего значащего разряда).
Стандартная запись табличного значения плотности:
ρтабл = (7,80 ± 0,05)·103 кг/м3
 |
Рис.2.3.
Интервалы на Рис. 2.3 частично перекрылись, поэтому можно сделать вывод о равенстве физических величин в пределах погрешностей измерений.
4. Правила построения графиков
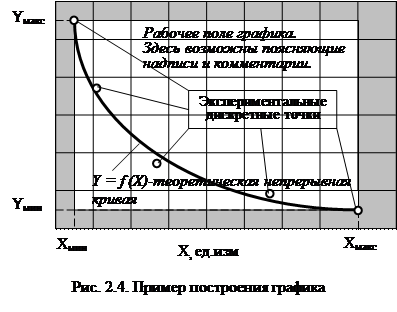
Графики в отличие от таблицы, дают более информативное представление об объекте измерения Y, если он представлен функциональной зависимостью Y = f(X) (Рис. 2.4.):
a) график позволяет находить значение функции Y = f(X) между значениями аргумента X1 и X2, которые экспериментально непосредственно не определялись (интерполяция);
b) график позволяет находить значение функции Y = f(X) за пределами интервала значений аргумента X, в котором были проведены измерения (экстраполяция).
При построении графиков обычно используют прямоугольную систему координат. Принято на горизонтальной оси откладывать независимую переменную - аргумент Х, а по вертикали – функцию Y.
Шкалы могут быть как равномерными, так и неравномерными. Может быть использована логарифмическая шкала (логарифм величин на одной оси) и двойная логарифмическая шкала (логарифм величин на обеих осях).
Построение графиков начинают с выбора масштабов для координатных осей таким образом, чтобы рабочее поле графика, включающее крайние значения отображаемых величин, занимало основную долю площади, ограниченную координатными осями.
Масштаб для каждой оси выбирают так, чтобы весь интервал соответствующих экспериментальных значений занимал большую часть оси. Практически надо взять разность максимального и минимального значений величины из таблицы и этот интервал использовать для выбора масштаба оси. При этом начало оси не обязательно должно совмещаться с нулевым значением величины.
Масштаб должен выбираться так, чтобы 1 см соответствовал 1, 2 или 5 единицам измерения, умноженным на соответствующую степень десяти, чтобы цифры у делений не были слишком длинными.
  |
После выбора масштаба каждую ось размечают, деля ее на равные промежутки и подписывая деления так, чтобы цифры не загромождали ось. В конце оси указывают обозначения величины и единицы измерения, вводя при необходимости степень десяти (10n).
Значения величины, имеющиеся в таблице, но не соответствующие делениям оси, на графике не пишут.
Так как результаты измерений имеют погрешности (Х±DХ, Y±DY), то на графике необходимо указать интервалы 2DХ и 2DY, в середине которых находятся средние значения измеряемых величин.
Экспериментальные точки наносят на график в выбранном масштабе. Затем эти точки соединяют плавными кривыми, проводя их в пределах погрешностей так, чтобы точки равномерно распределились по обе стороны кривой.
Нельзя соединять точки ломаной линией, т.к. в большинстве случаев физические зависимости описываются плавными кривыми, а разброс точек относительно кривой объясняется случайными погрешностями эксперимента.
5. Определение параметров функциональных зависимостей
Если изучаемые величины связаны функциональной зависимостью 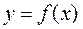 , то в табл.1 вводят столбцы для аргумента
, то в табл.1 вводят столбцы для аргумента 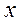 и функции
и функции 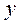 . Строка «среднее» не заполняется, а погрешность определяется для одного (любого) опыта.
. Строка «среднее» не заполняется, а погрешность определяется для одного (любого) опыта.
Например, если изучаемые в эксперименте величины 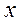 и
и 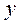 связаны функциональной зависимостью вида
связаны функциональной зависимостью вида 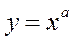 или
или 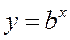 , то обычно целью эксперимента является установление коэффициентов a и b.
, то обычно целью эксперимента является установление коэффициентов a и b.
Наиболее просто и достаточно точно можно получить искомые параметры, исследуя графики соответствующих зависимостей.
Логарифмируя выражение 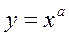 , получим:
, получим:
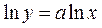 , откуда
, откуда 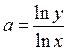 .
.
Логарифмируя выражение 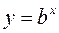 , получим:
, получим:
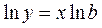 , откуда
, откуда 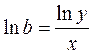 , потенцируя получают b.
, потенцируя получают b.
Кроме графической аппроксимации возможно применение метода численного сглаживания экспериментальных зависимостей (метод наименьших квадратов)
6. Метод наименьших квадратов
Под методом наименьших квадратов понимается определение неизвестных параметров a, b, c,… принятой функциональной зависимости
y = f(x,a,b,c,…),
которые обеспечивали бы минимум среднего квадрата (дисперсии) ошибки
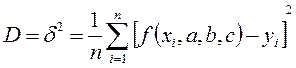 , (24)
, (24)
где xi, yi – совокупность пар чисел, полученных из эксперимента.
Так как условием экстремума функции нескольких переменных является условие равенства нулю ее частных производных, то параметры a, b, c,… определяются из системы уравнений:
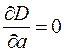 ;
; 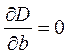 ;
; 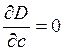 ; … (25)
; … (25)
Необходимо помнить, что метод наименьших квадратов применяется для подбора параметров после того, как вид функции y = f(x) определен.
Если из теоретических соображений нельзя сделать никаких выводов о том, какой должна быть эмпирическая формула, то приходится руководствоваться наглядными представлениями, прежде всего графическим изображением наблюденных данных.
На практике чаще всего ограничиваются следующими видами функций:
1) линейная 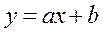 ;
;
2) квадратичная  ;
;
3) гипербола 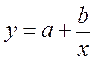 ;
;
4) показательная 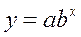 .
.
Пример: Требуется определить вид и параме________ Конец 1 лекции ___________