ВВЕДЕНИЕ. ИСХОДНЫЕ ПОНЯТИЯ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ.

Процессы принятия решений являются основой любой деятельности. При формировании как стратегических, так и тактических решений необходимо учитывать многочисленные факторы, опираясь на критерий эффективности путей достижения цели, оптимизируя решение на основе исследования операций.

Исследование операций – научный подход к решению задач организационного управления, предполагающий:

1 Построение математических, экономических, статистических моделей с целью принятия решений и управления в сложных ситуациях или условиях неопределенности.

2 Изучение взаимосвязей, определяющих возможные последствия от принятия решений, установление критериев эффективности, позволяющих оценить преимущества вариантов действий.

Человек принимает решение на основе информации о состоянии объекта управления и внешней среды, информации от вышестоящих органов управления. Анализируя эту информацию, человек производит постановку задачи, решение которой позволит наилучшим образом осуществлять управление производством в данной конкретной ситуации. На основании полученных данных и заданного критерия эффективности выбирается то решение, результат которого наилучшим образом удовлетворяет заданным условиям.

Задача принятия решения – это задача, сформулированная в терминах цели, средств, результатов. Принятие решения – выбор какого-то варианта из имеющихся действий или так называемого множества альтернатив. Тот, кто производит выбор и несет за него ответственность, является лицом, принимающим решения. Это может быть человек, коллектив, устройство, система принятия решений.

Эксперт – специалист, дающий оценки альтернатив. необходимые для формирования матриц альтернатив, которые являются исходной информацией задачи выбора.

Консультант – специалист, разрабатывающий модель исходной задачи, процедуру принятия решения, организующий работу системы принятия решений.

Общей задачей принятия решения (ЗПР) могут быть неизвестные множества альтернатив и принцип оптимальности. Задача с известным множеством альтернатив называется задачей выбора. Задача с известным множеством Х альтернатив и известным критерием оптимальности (эффективности) называется общей задачей оптимизации. Для математической модели ЗПР формальное описание средств и результатов можно задать двумя множествами: множеством альтернатив Х и множеством исходов А. Элементы этих множеств могут быть взаимосвязаны следующим образом:

1 Функционально, т.е. каждая альтернатива приводит к единственному исходу, тогда принятие решений происходит в условиях определенности.

2 Стохастически, когда каждая альтернатива с определенной вероятностью приводит к одному из нескольких исходов, тогда принятие решения происходит в условиях риска.

3 Неопределенно, когда каждая альтернатива может привести к одному из нескольких исходов при помощи недостаточно формализованных понятий и отношений, тогда принятие решений происходит в условиях нечеткой неопределенности.

Задача принятия решения может быть задана следующими способами:

1 Указывается граф связи альтернатив с исходами. Альтернативы являются начальными вершинами дуг графа, исходы – конечными. Вес дуги показывает вероятность исхода a_i при выборе альтернативы x_j.

2 Указывается функция реализации. Если известно множество Y состояний среды, тогда функция исходов задается в виде таблицы:

у х	Y₁	Y₂	…	Y_к
Х₁	F(Х₁, Y₁)	F(Х₁, Y₂)	…	F(Х₁, Y_к)
Х₂	F(Х₂, Y₁)	F(Х₂, Y₂)	…	F(Х₂, Y_к)
…	…	…	…	…
Х_n	F(Х_n, Y₁)	F(Х_n, Y₂)	…	F(Х_n, Y_к)

3 Ставится задача оптимизации f(x₁,…,x_n) →opt ( 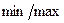) при некоторых условиях для x₁,…,x_n .

В зависимости от степени информированности о состоянии среды функции реализации могут быть различны. В условиях определенности F зависит только от альтернатив. В условиях риска, когда известны вероятности появления У_j состояния среды, задается закон распределения этих состояний. В условиях неопределенности задается лишь таблица функции реализации.

Пример. Задача о замене вратаря.

На последней минуте матча счет 1:1, и тренер должен принять решение о том, заменить вратаря или нет. Известны связи альтернатив и исходов:

альтернативы: Х₁- заменить вратаря; Х₂-не менять;

исходы: В – выигрыш; Н – ничья ; П – проигрыш.

Граф связи: Х₁ 1/3 П

1/2 1/8

1/6 В 7/8 Х₂

Состояния среды:

У₁: x₁→B, х₂ →Н У₄: х₁ →B, х₂ →П

У₂: x₁→H, х₂ →Н У₅: х₁ →Н, х₂ →П

У₃: x₁→П, х₂ →Н У₆: х₁ →П, х₂ →П

Находим вероятности состояний:

Р(У₁)=1/6*7/8 =7/48 Р(У₄)=1/6*1/8=1/48

Р(У₂) =1/2*7/8=7/16 Р(У₅)=1/2*1/8=1/16

Р(У₃) =1/3*7/8=7/24 Р(У₆)=1/3*1/8=1/24

Таблица функции реализации примет вид:

у х	У₁	У₂	У₃	У₄	У₅	У₆
Х₁	В	Н	П	В	Н	П
Х₂	Н	Н	Н	П	П	П

Из полученных результатов следует, что при выборе альтернативы Х₂ вероятность проигрыша меньше.

В формулировке основателя кибернетики Винера поведение можно подразделить на целенаправленное, допускающее истолкование как направленное на достижение цели и конечного состояния, когда объект связан в пространстве и во времени с другими объектами или событиями, и нецеленаправленное, т.е. случайное.

Цель определяет желаемое состояние системы или желаемый результат ее поведения. На основании поставленной цели формируется критерий эффективности (оптимальности), и принимается решение, соответствующее этому критерию и приводящее к заданной цели.

Существует следующая классификация типов целей:

1 По характеру информации:

- качественная цель характеризуется тем, что всякий возможный исход либо полностью удовлетворяет, либо полностью не удовлетворяет этой цели, причем исходы, удовлетворяющие цели не различимы между собой по степени выполнения этой цели;

- количественная цель характеризуется максимизацией (минимизацией) заданной функции цели.

2 По характеру выполнения:

- промежуточные;

- конечные.

3 По степени важности:

- основные;

- дополнительные (частные).

Выбор является действием, придающим деятельности целенаправленность.

Существует три основных языка описания выбора альтернативы:

1 Критериальный. Каждую альтернативу оценивают отдельным числом, значением критерия, и на основе функции цели, которая может быть функцией предпочтения, полезности или критерия качества выбирают оптимальную альтернативу. Критерий – это правило, по которому отбираются средства достижения цели. Если цель указывает желаемое состояние системы, то критерий – эффективный способ его достижения. Критерий позволяет выбрать средства достижения цели и ответить на вопрос, какой ценой она может быть достигнута.

2 Язык бинарных отношений. Для любой пары альтернатив устанавливается либо отношение предпочтения или отношение равноценности либо несравнимость, и выявляются наиболее предпочтительные альтернативы по рассмотренному отношению R, которое позволяет придавать разный смысл понятиям наилучший, оптимальный.

return false">ссылка скрыта

3 Язык функции выбора. Находится в стадии разработки.

Для выбора оптимального решения из всего множества применяют один из следующих методов принятия решений:

1 Использование накопленного опыта.

2 Интуитивное решение задачи человеком, имеющим определенный опыт и теоретические знания, внутреннее чутье, проницательность; человек не может обосновать решение, хотя оно правильное.

3 Принятие решения на основе здравого смысла, обоснованной последовательности рассуждений на содержательном уровне.

4 Научный подход, при котором проблема подвергается количественному анализу. Решение может быть получено с математической строгостью и с минимальными затратами времени и ресурсов, но требует большой переработки информации, и поэтому связано с применением ЭВМ. В рамках этого подхода стоится математическая модель управляемой системы, проводится системный анализ на основе теории системного анализа и этот подход предполагает следующие этапы:

1) Постановка задачи.

2) Структуризация системы – локализация и установление границ элементов системы, разбиение ее на подсистемы, установление ее приоритетов, определение существующих связей исследуемой системы с внешней средой, входных и выходных параметров.

3) Построение модели, облегчающей понимание системы, позволяющей провести исследование, проанализировать поведение, изменять ее параметры, вводить некоторые воздействия с целью изучения реакции системы на эти воздействия. При этом определяются необходимые изменения для оптимизации функционирования.

В зависимости от используемых сведений о состояниях управляемой системы, системы делятся на классы:

I Системы с обратной связью. После каждой реализации решения, сведения о состоянии системы передаются в систему управления по каналу обратной связи для анализа и учета при выборе последующих воздействий.

1 Системы стабилизации. Управляющие воздействия являются числами. (Например, системы поддержания температуры).

2 Системы с программным управлением. Управляющее воздействие – функции некоторых параметров, зависящих от состояния системы. (Например, системы обработки деталей на станках с числовым программным управлением).

3 Следящие системы предназначены для измерения состояния объекта по заранее неизвестному закону, определяемому внешней средой, управляющим воздействием является функция времени. ( Например, радиолокаторы, системы управления ПВО).

II Разомкнутые системы используют методы управления по жесткой программе и методы, основанные на устранении воздействия случайных возмущений. (Например, светофор, система отопления)[31]

Процесс функционирования системы принятия решений изобразим на рисунке 1.

Рисунок 1 – Схема функционирования системы принятия решений

Рассмотрим классификацию методов решения задач выбора (см. рис. 2) [28].

В условиях коалиционный адаптация определенности голосование по решениям обработка мнений экспертов селекция

упорядочивание

оптимизация

конфликтный

математическое игры с природой

программирование игры с противником

комбинаторная

оптимизация

В условиях неопределенности

расплывчатость (нечеткость)

теория расплывчатых множеств

теория нечетких критериев

неизвестность

теория игр

теория полезности

стохастичность

теория стохастических

решений

Рисунок 2 - Схема классификации методов решения задач выбора