Вычислим комплексное сопротивление

Z = R1 + = R1 + =

 

= R1 + = R1 + =

= 10 + 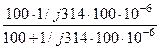= 19,2-j28,9.

Определяем комплексное значение тока

İ =

= 0,319 + j0,48 = 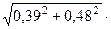e jarctg 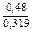= 0,57ej56,4 .

 

Задача № 3

 

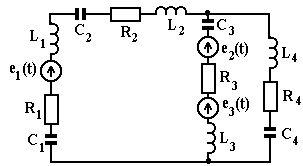
Для цепи, изображенной на рис. 2.6, используя метод кон-турных токов, рассчитайте комплексные амплитуды токов во всех ветвях, определив ее параметры по формулам

хс = 2 · N + n [ КОм], хL = + n [ КОм],

R = 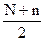[ КОм], е1( t ) = Ncos106t,

e2 ( t ) = - sin 106t, e3 ( t ) = cos 106t,

 
 

где N – номер фамилии студента по журналу или две последние цифры номера зачетной книжки, n – номер элемента в схеме.

.

Рис. 2.6

Основные положения и соотношения

Для определения токов и напряжений в электрической цепи по методу контурных токов используется второй закон Кирхгофа. На его основе составляется система уравнений для независимых контуров схемы. Из решения системы определяются контурные токи и на основании их вычисляются токи во всех ветвях электрической цепи.

Пример № 1

 
 

Используя метод контурных токов, определить токи в ветвях схемы

 
 

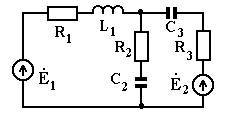Рис. 2.7

 

Ė1= 10 В, Ė2 = 20 В, L1 = 10 мГн, C1= C2 =100 мкФ,

ω =10 рад/сек, R1= 50 Ом, R2= 5 Ом, R3=10 Ом.

Решение

Представим ветви в схеме рис. 2.7 в виде комплексных сопротивлений Z1, Z2, Z3.

 
 

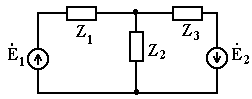Рис. 2.8

Определим значения комплексных сопротивлений Z1,.Z2, Z3.

 

Z1 = R1 + jωL1 = 50 + j103 ∙ 10 ∙ 10-5 = 60 + j10,

Z2 = R2 + ,

Z3 = R3 + .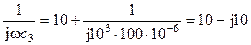

Составим систему уравнений по методу контурных токов, приняв за контурные токи: İ1 в контуре Ė1, Z1, Z2 и İ2 в контуре Е2, Z2, Z3 (рис. 2.9).

Рис. 2.9

 
 


İ1 ( Z1 + Z2 ) - İ2 Z2 = Ė1

İ2 ( Z2 + Z3 ) – İ1 Z2 = Ė2.

 

Перепишем систему уравнений в виде

 
 


İ1( Z1 + Z2 ) - İ2 Z2 = Ė1

- I1 Z2 + I2 (Z2 + Z1) = Ė2.

 

Решим эту систему уравнений, используя метод Крамера, записав матрицу сопротивлений в виде

( Z1 + Z2 ) ( -Z2 )

( -Z2 ) ( Z2 + Z3 ) .

 

Подставляя значения сопротивлений Z1, Z2, Z3 в матрицу, получим

( 65 ) ( -5 + j10 )

( -5 +j10 ) ( 15 - j20 ) .

 

Найдем определитель матрицы ∆

 

( 65 ) ( -5 + j10 )

∆ = = 1050 – j1200.

( -5 +j10) ( 15 – j20)

 

Находим определители ∆ İ1 и ∆ İ2

               
     
   
 
 
 


Ė1 ( -Z2 ) ( 10 ) ( -5 + j10 )

∆ İ1 = = =250-j400,

Ė2 ( Z2 + Z3) ( 20 ) ( 15 – j20)

 

               
       
 
 


( Z1 + Z2 ) Ė1 ( 65 ) (10 )

∆ İ2 = = =1350-j100,

( -Z2 ) Ė2 ( -5 + j10) ( 20 )

 

В соответствии с формулами Крамера находим контурные токи İ1 и İ2, т.е.

İ1 = 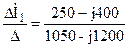= 0,292 – j0,047 A,

İ2 = = 1,258 + j0,144 A.

Ток в ветви Z2 найдем как алгебраическую сумму токов İ1 и I2, т.е.

 

İZ2 = İ2 - İ1 = 1,258 + j0,144 – 0,292 + j0,047 =0,966 +j0,191 А.

 

Таким образом получаем, что

 

İZ1 = İ1 = 0,292 – j0,047 A,

İZ2 = İ2 = 1,258 + j0,144 A,

IZ2 = İ2 – I1 = 0,966 + j0,191 A.

 

Задача № 4

 

Замкните накоротко все элементы в схеме рис. 2.6, кроме e1(t), L1 , R1 , C2 , R2. Изобразите полученную схему. Выясните, какой тип контура получился. Определите напряжение на реактивных элементах при резонансе. Для полученного контура определите следующие величины:

резонансную частоту;

абсолютную, относительную и обобщенную расстройки;

добротность контура;

полосу пропускания контура;

характеристическое сопротивление;

сопротивление контура при резонансе.

Параметры элементов контура определить по формулам

xc = 2 ∙ N + n [KOм], xL = + n [KOм],

R = 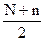[Oм], e1( t ) = Ncos 106t, где N – номер фамилии студента по журналу или две последние цифры номера зачетной книжки, n – номер элемента в схеме.

Основные положения и соотношения

 

Чтобы получить в реальном контуре колебания с постоянной амплитудой, необходимо включить в него источник э.д.с., который к началу каждого периода восполнял бы потери энергии, происшедшие за предыдущий период. Если источник э.д.с. соединяется последовательно с катушкой индуктивности

 
 

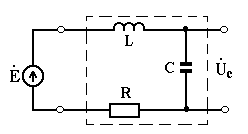и конденсатором, то цепь называется контуром с последовательно включенными элементами, т.е. последовательным контуром. Этот контур представляется в виде 4-х полюсника, ко входным зажимам которого подключен источник гармонической э.д.с. Ė, а выходное напряжение 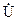снимается с конденсатора С ( рис. 2.10 ) или с L.

 

 
 

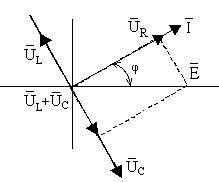Рис. 2.10

Комплексное сопротивление такой цепи равно

Z = R + jωL + 1/jωC = R + j(ωL - 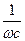) = R +jx.

При х = ω0L – 1/ω0C = 0 наступает резонанс напряжений, при этом ω0 называется собственной частотой контура.

Условием резонанса является равенство (совпадение) частоты питающего генератора ωr и собственной частоты контура ( частоты свободных колебаний ω0).

Величины напряжений на индуктивности и емкости при резонансе равны и противоположны друг другу. Они могут быть определены как

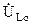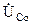= - = jω0L = jE = jE 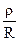= jEQ.

Векторная диаграмма при резонансе выглядит следующим образом ( рис. 2.11), где Io = E/R.

Напряжение на конденсаторе и индуктивности в Q раз превышает напряжение Е, приложенное к колебательному контуру.

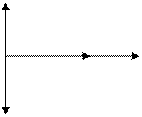ŪLo

 

Ī0

0 Ē

 

ŪCo

 

Рис. 2.11

 

Поэтому резонанс в последовательном контуре называют резонансом напряжений.

При частоте генератора ωr < ω0 векторная диаграмма последовательного контура приобретает вид ( рис. 2.12 ).

 

Рис. 2.12

 

Здесь φ – угол сдвига фаз между током в контуре İ и напряжением источника Е. Сопротивление контура носит емкостной характер.

При частоте генератора ωr > ω0 векторная диаграмма видоизменяется ( рис. 2.13 ).

 

 

Рис. 2.13

 

В этом случае сопротивление контура носит индуктивный характер.

Входное сопротивление и проводимость последовательного контура определяются соответственно выражениями

 

Z = R +jx = 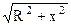∙ ejarctg x / R,

= e-jarctg x / R.

Величина x /R обозначается через ξ и называется обобщенной расстройкой. Она может быть отрицательной, когда ω < ω0 и положительной, когда ω > ω0. При резонансе ξ = 0. Безразмерная величина ξ служит мерой отличия частоты контура от частоты подведенных колебаний. Отношение величины у = 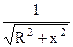= 107 рад/с;

f0 = ≈ 1,6 ∙ 106 Гц = 1,6 МГц ;

ρ = = 1000 Ом ;

d = = 0,01; Q =

I0 =

P0 = 0,12 ∙ 10 = 0,1 Вm;

UL0 = UC0 = I0 ∙ ρ = 0,1 ∙ 1000 = 100 В;

 
 

Δω = ω – ω0 = 1,002 ∙ 107 – 107 = 0,002 ∙ 107 рад/с.

ν = = 2

.