Алгоритмы растеризации

Прежде чем перейдем к непосредственному рассмотрению возможности перевода ма­тематического описания объекта (линии и пр.) в растровую форму рассмотрим понятие связанности. Связность – возможность соедине­ния двух пикселей растровой линией, т. е. последовательным набором пик­селей. Возникает вопрос, когда пиксели (x₁, y₁) и (x₂, y₂) можно считать со­седними. Для этого вводятся два понятия связности:

1. 4-связность: пиксели считаются соседними, если либо их x-координаты, либо их y – координаты отличаются на единицу:

|x₁­ – x₂| + |y₁ – y₂| ≤ 1;

2. 8-связность: пиксели считаются соседними, если их x-координаты и y-координаты отличаются не более чем на единицу:

|x₁­ – x₂| ≤ 1, |y₁ – y₂| ≤ 1.

На рис. 2.2 изображены 4-связная линия (а) и 8-связная линия (б).

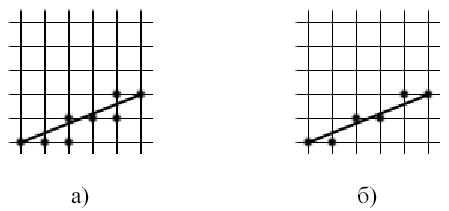
Рис. 2.2 4-связная линия (а) и 8-связная линии

При переводе объектов в растровое представление существуют, алгоритмы, как использующие 4-связанность, так использующие 8-связон­ность.

2.1.1. Растровое представление отрезка. Алгоритм Бре­зенхейма

Рассмотрим задачу построения растрового изображения отрезка, соеди­няющего точки A(x_a, y_a) и B(x_b, y_b). Для простоты будем считать, что

0 ≤ y_b – y_a ≤ x_b – x_a . Тогда отрезок описывается уравнением:

y = y_a + 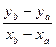(x–x_a), x Є [x_a, x_b], или y = kx + b

Отсюда получаем простейший алгоритм растрового представления от­резка:

void line(int xa, int ya, int xb, int yb, int color)

{

double k = ((double)(yb – ya)) / (xb – xa);

double b = ya – k * xa;

for (int x = xa; x <= xb; x++)

putpixel(x, (int)(k * x + b), color);

}

Вычислений значений функции y = kx + b можно избежать, используя в цикле рекуррентные соотношения, так как при изменении x на 1 значение y меняется на k.

Void line(int xa, int ya, int xb, int yb, int color)

{

double k = ((double)(yb – ya)) / (xb – xa);

double y = ya;

for (int x = xa; x <= xb; x++, y += k)

putpixel(x, (int)y, color);

}

Приведенные простейшие пошаговые алгоритмы построения отрезка имеют ряд недос­татков:

1. Выполняют операции над числами с плавающей точкой, а жела­тельно было бы работать с целочислен­ной арифметикой;

2. На каждом шаге выполняется операция округления, что также снижает быстро­действие.

Эти недостатки устранены в следующем алгоритме Брезенхейма.

Как и в предыдущем случае будем считать, что тангенс угла наклона от­резка принимает значение в диапазоне от 0 до 1. Рассмотрим i шаг алго­ритма (Рис 2.3.). На этом этапе пиксель P_i-1 уже найден как ближайший к ре­аль­ному отрезку. Требуется определить ка­кой из пикселов T_i или S_i будет ус­тановлен следующим.

 

Рис. 2.3 i шаг алгоритма Брезенхейма

В алгоритме используется управляющая переменная d_i, которая на каждом шаге про­порциональна разности ме­жду S и T. Если S < T, то S_i ближе к от­резку, иначе выбирается T_i.

Пусть изображаемый отрезок проходит из точки (x₁, y₁) в точку (x₂, y₂). Ис­ходя из на­чальных условий точка (x₁, y₁) ближе к началу координат. Тогда перенесем оба конца от­резка с помощью преобразования T(­­­­­­–x₁, –y₁), так чтобы первый конец отрезка совпал с началом координат. Начальной точкой отрезка стала точка (0, 0), конечной точкой (dx, dy), где dx = x₂ – x₁, dy = y₂ – y₁ (Рис 2.4.).

Рис. 2.4 Вид отрезка после переноса в начало координат

Уравнение прямой в этом случае будет иметь вид:

y=x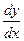

Обозначим координаты точки P_i-1 после переноса через (r, q). Тогда S_i = (r+1, q) и T_i = (r+1, q+1).

Из подобия треугольников на рис 2.4. можно записать

=

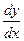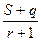
Выразим S

S = 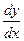(r + 1) – q

T можно представить как T = 1 – S. Используем предыдущую формулу

T = 1 – S = 1 – 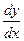(r + 1) – q

Найдем разницу S – T

S – T = 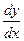(r + 1) – q – 1 + 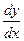(r + 1) – q = 2 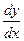(r + 1) – 2 q – 1

Помножим левую и правую часть на dx

dx (S – T) = 2 dy (r + 1) – 2 q dx – dx = 2(r dy – q dx) + 2 dy – dx

Величина dx положительная, поэтомунеравенство dx (S – T) < 0 можно ис­пользовать в качестве проверки при вы­боре S_i. Обозначим d_i = dx (S – T), тогда

 

d_i = 2(r dy – q dx) + 2 dy – dx

Поскольку r = x_i-1 и q = y_i-1, то

 

d_i = 2 x_i-1 dy –2 y_i-1 dx + 2 dy – dx

Прибавляя 1 к каждому индексу найдем d_i+1

 

d_i+1 = 2 x_i dy –2 y_i dx + 2 dy – dx

Вычитая d_i из d_i+1 получим

 

d_i+1– d_i = 2 dy (x_i – x_i-1) – 2 dx (y_i – y_i-1)

 

Известно, что x_i – x_i-1 = 1, тогда

 

d_i+1– d_i = 2 dy – 2 dx (y_i – y_i-1)

 

Отсюда выразим d_i+1

 

d_i+1 = d_i + 2 dy – 2 dx (y_i – y_i-1)

 

Таким образом, получили итеративную формулу вычисления управляющего коэффициента d_i+1, по предыдущему значению d_i. С помощью управляющего коэффициента выбирается следующий пиксель S_i или T_i.

Если d_i ≥ 0, тогда выбирается T_i и y_i = y_i–1 + 1 и d_i+1 = d_i +2 (dy – dx). Если d_i < 0, тогда выбирается S_i и y_i = y_i–1 и d_i+1 = d_i +2 dy.

Начальные значения d₁ с учетом того, что (x₀, y₀) = (0, 0)

d₁ = 2 dy – dx

Преимуществом алгоритма является то, что для работы алгоритма требу­ются минимальные арифметические воз­можности: сложение, вычитание и сдвиг влево для ум­ножения на 2.

Реализация этого алгоритма на C++ выглядит следующим образом.

 

void MyLine ( int x1, int y1, int x2, int y2, int color )

{

int dx = abs ( x2 - x1 );

int dy = abs ( y2 - y1 );

int sx = x2>=x1?1:-1;

int sy = y2>=y1?1:-1;

if(dy<=dx)

{

int d = ( dy<<1 ) - dx;

int dl=dy<<1;

int d2 = (dy-dx)<<1;

putpixel(x1,y1,color);

for (int x = x1 + sx, y = y1, i = 1; i<= dx;i++,x+=sx)

{

if(d>0)

{

d+= d2;

y+= sy;

}

else d+=dl;

putpixel(x,y,color );

}

}

else

{

int d=(dx<<1) - dy;

int dl=dx<<1;

int d2=(dx-dy)<<1;

putpixel( x1, y1, color );

for ( int x = x1 , y = y1 + sy, i=1 ; i <=dy; i++,y+=sy )

{

if(d>0)

{

d += d2;

x += sx;

}

else

d+=dl;

putpixel ( x, y, color );

}

}

}

Если dy > dx, то необходимо будет использовать этот же алгоритм, но по­шагово увели­чивая y и на каждом шаге вычислять x.