Область допустимых решений задачи

Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что данная задача линейной оптимизации имеет множество допустимых решений, т.е. многовариантна. Нам же необходимо найти максимальное и минимальное значение целевой функции в построенной области.

Для целевой функции найдем вектор, показывающий направление наибольшего ее изменения, который называется вектором градиента. Вектор-градиент целевой функции имеет координаты =(40;50). Изобразим вектор и построим линию уровня – прямую перпендикулярную этому вектору (см. график). Для нахождения максимума целевой функции будем перемещать линию уровня параллельно самой себе в направлении вектора-градиента. Последняя точка многоугольника решений, которую пересечет линия уровня, является угловая точка В. Следовательно, в точке В функция достигает максимального значения.

Для нахождения координат точки В необходимо решить систему из уравнений тех прямых, которые пересекаются в данной точке:

Решив эту систему, получим, что =17,14; 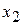=23,57.

Следовательно, максимальное значение целевая функция достигает в точке и равно .

Для нахождения минимального значения целевой функции необходимо перемещать линию уровня параллельно самой себе в противоположном направлении вектора-градиента, увидим, что последней точкой многоугольника решений является угловая точка О. Следовательно, в точке О функция достигает минимального значения.

Координаты точки О видны из чертежа.

Следовательно, минимальное значение целевая функция достигает в точке и равно .