ДИФФЕРЕНЦИАЛЬНЫЕ КРИТЕРИИ
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
Множество  называется выпуклым, если с любыми двумя точками
называется выпуклым, если с любыми двумя точками  оно содержит отрезок, их соединяющий. Иначе это определение можно сформулировать так: множество
оно содержит отрезок, их соединяющий. Иначе это определение можно сформулировать так: множество  выпукло, если
выпукло, если 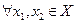 точка
точка 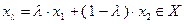 при всех
при всех 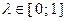 . На рис. 3.1.1 представлена геометрическая иллюстрация выпуклого и невыпуклого множеств.
. На рис. 3.1.1 представлена геометрическая иллюстрация выпуклого и невыпуклого множеств.

Рис. 3.1.1. Геометрическая иллюстрация выпуклого (а) и невыпуклого (б) множеств
Пространство  образует выпуклое множество. Пустое множество и множество, состоящее из одной точки, удобно считать выпуклыми. Тогда из определения выпуклого множества следует, что пересечение любого числа выпуклых множеств является выпуклым множеством.
образует выпуклое множество. Пустое множество и множество, состоящее из одной точки, удобно считать выпуклыми. Тогда из определения выпуклого множества следует, что пересечение любого числа выпуклых множеств является выпуклым множеством.
Функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется выпуклой на этом множестве, если
, называется выпуклой на этом множестве, если 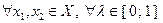 выполнено неравенство
выполнено неравенство
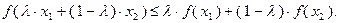 (3.1.1)
(3.1.1)
На рис. 3.1.2 в качестве примера приведен график выпуклой функции одной переменной  . Выпуклую функцию можно определить как функцию,
. Выпуклую функцию можно определить как функцию,
|

Рис. 3.1.2. Пример выпуклой функции одной переменной
над графиком которой – выпуклое множество.
Функция  называется вогнутой на выпуклом множестве
называется вогнутой на выпуклом множестве  , если функция
, если функция 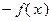 выпукла на
выпукла на  . Вогнутую функцию можно определить также как функцию, под графиком которой – выпуклое множество.
. Вогнутую функцию можно определить также как функцию, под графиком которой – выпуклое множество.
Существуют подклассы выпуклых функций. Так, функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется строго выпуклой на
, называется строго выпуклой на  , если
, если 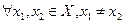 и
и 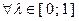 равенство в (3.1.1) имеет место только при
равенство в (3.1.1) имеет место только при 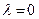 и
и  .
.
Функция  называется строго вогнутой на выпуклом множестве
называется строго вогнутой на выпуклом множестве  , если функция
, если функция 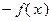 строго выпукла на
строго выпукла на  .
.
Например, функция одной переменной  является одновременно выпуклой и вогнутой на
является одновременно выпуклой и вогнутой на 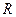 , однако не является ни строго выпуклой, ни строго вогнутой.
, однако не является ни строго выпуклой, ни строго вогнутой.
Функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется сильно выпуклой (сильно выпуклой с константой
, называется сильно выпуклой (сильно выпуклой с константой 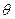 ) на
) на  , если
, если 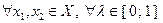 выполнено неравенство
выполнено неравенство
 (3.1.2)
(3.1.2)
где 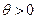 ,
, 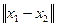 – евклидова норма (длина вектора):
– евклидова норма (длина вектора):
 (3.1.3)
(3.1.3)
Функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется сильно вогнутой на этом множестве, если функция
, называется сильно вогнутой на этом множестве, если функция 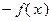 сильно выпукла на
сильно выпукла на  .
.
Функция, сильно выпуклая на множестве  , является выпуклой и строго выпуклой на этом множестве.
, является выпуклой и строго выпуклой на этом множестве.
Пример 3.1.1. Показать, что функция одной переменной  сильно выпукла на
сильно выпукла на 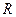 .
.
Левая часть неравенства (3.1.2) в данном случае принимает вид:
 . (3.1.4)
. (3.1.4)
Вычитая выражение (3.1.4) из первых двух слагаемых правой части неравенства (3.1.2), получим:
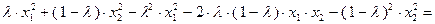
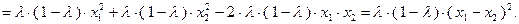
Таким образом, неравенство (3.1.2) превращается в тождественное равенство при  и, следовательно, функция
и, следовательно, функция  является сильно выпуклой на
является сильно выпуклой на 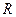 с константой
с константой  .
.
В практических задачах важное значение имеет выяснение наличия у исследуемых функций свойств выпуклых функций, либо их отсутствия.
Рассмотрим некоторые теоремы, которые могут быть использованы для проверки выпуклости функций.
Теорема 3.1.1
Пусть функции 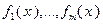 – выпуклы на множестве
– выпуклы на множестве  и числа
и числа 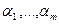 неотрицательны. Тогда функция
неотрицательны. Тогда функция
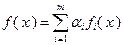
выпукла на множестве  . Читателю предлагается доказать эту теорему самостоятельно.
. Читателю предлагается доказать эту теорему самостоятельно.
Теорема 3.1.2
Дана функция  , обладающая следующими свойствами:
, обладающая следующими свойствами:
1) функция  определена на множестве
определена на множестве 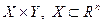 ,
,  – выпуклое множество;
– выпуклое множество;
2) функция  выпукла по
выпукла по 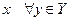 ;
;
3) функция  ограничена сверху по
ограничена сверху по 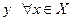 .
.
Тогда функция 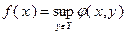 выпукла на множестве
выпукла на множестве  .
.
Доказательство. Для любых точек  и для любого
и для любого 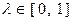 можно записать:
можно записать:
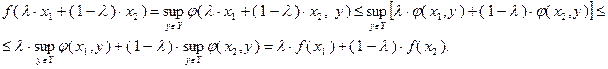
Таким образом, неравенство (3.1.1) выполнено, и, следовательно, теорема доказана.
В случае 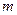 функций одной переменной
функций одной переменной  , рассматривая индекс
, рассматривая индекс 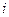 в качестве аналога переменной
в качестве аналога переменной 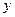 из теоремы 3.1.2, завершающую часть формулировки этой теоремы можно записать в виде заключения о выпуклости функции
из теоремы 3.1.2, завершающую часть формулировки этой теоремы можно записать в виде заключения о выпуклости функции
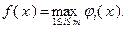
На рис. 3.1.3 представлены графики двух выпуклых функций одной переменной  и
и 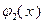 . График, показанный сплошной линией, является графиком функции
. График, показанный сплошной линией, является графиком функции
 ,
,
которая согласно теореме 3.1.2 является выпуклой.
Теорема 3.1.3
Пусть функция 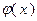 выпукла на выпуклом множестве
выпукла на выпуклом множестве 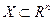 , а функция
, а функция 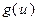 выпукла и монотонно не убывает на выпуклом множестве
выпукла и монотонно не убывает на выпуклом множестве 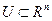 , причем
, причем 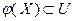 . Тогда функция
. Тогда функция  выпукла на множестве
выпукла на множестве  .
.

Рис. 3.1.3. Пример применения теоремы 3.1.2 для случая двух функций одной переменной
Доказательство. 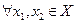 и
и 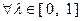 можно записать:
можно записать:
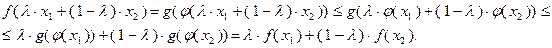 (3.1.5)
(3.1.5)
Первое из приведенных неравенств справедливо на том основании, что, во-первых,
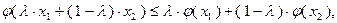
так как функция 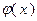 выпукла, и, во-вторых, что функция
выпукла, и, во-вторых, что функция 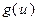 монотонно не убывает. Справедливость второго неравенства в (3.1.5) объясняется выпуклостью функции
монотонно не убывает. Справедливость второго неравенства в (3.1.5) объясняется выпуклостью функции 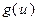 . Теорема доказана.
. Теорема доказана.
Применение рассмотренных теорем к решению практических задач продемонстрируем на следующем примере.
Пример 3.1.2. Выяснить, является ли выпуклой функция
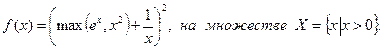
Функция 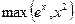 является выпуклой по теореме 3.1.2. Функция
является выпуклой по теореме 3.1.2. Функция  выпукла в соответствии с теоремой 3.1.1. Наконец, функция
выпукла в соответствии с теоремой 3.1.1. Наконец, функция  , где
, где  , является выпуклой по теореме 3.1.3. Таким обрзом, заданная в примере функция выпукла.
, является выпуклой по теореме 3.1.3. Таким обрзом, заданная в примере функция выпукла.
Следующую теорему читателю предлагается доказать самостоятельно.
Теорема 3.1.4
1. Пусть функция  является строго выпуклой на выпуклом множестве
является строго выпуклой на выпуклом множестве  . Тогда
. Тогда  функция
функция  строго выпукла на
строго выпукла на  .
.
2. Пусть функция  является сильно выпуклой с константой
является сильно выпуклой с константой 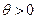 на выпуклом множестве
на выпуклом множестве  . Тогда
. Тогда  функция
функция  сильно выпукла с константой
сильно выпукла с константой  на
на  .
.
3. Пусть функция  выпукла на выпуклом множестве
выпукла на выпуклом множестве  , а функция
, а функция  сильно выпукла с константой
сильно выпукла с константой 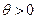 на
на  . Тогда функция
. Тогда функция  является сильно выпуклой с константой
является сильно выпуклой с константой 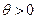 на
на  .
.
4. Пусть функция  выпукла на выпуклом множестве
выпукла на выпуклом множестве  , а функция
, а функция  строго выпукла на
строго выпукла на  . Тогда функция
. Тогда функция  является строго выпуклой на
является строго выпуклой на  .
.
p>Заметим, что линейная функция
 является одновременно выпуклой и вогнутой на выпуклом множестве
является одновременно выпуклой и вогнутой на выпуклом множестве  и что только линейные функции обладают таким свойством. При этом линейная функция не является ни строго выпуклой (вогнутой), ни сильно выпуклой (вогнутой). Всякая сильно выпуклая функция является строго выпуклой, но не наоборот. Например, функция
и что только линейные функции обладают таким свойством. При этом линейная функция не является ни строго выпуклой (вогнутой), ни сильно выпуклой (вогнутой). Всякая сильно выпуклая функция является строго выпуклой, но не наоборот. Например, функция  строго выпукла на
строго выпукла на 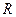 , но не является сильно выпуклой.
, но не является сильно выпуклой.
ДИФФЕРЕНЦИАЛЬНЫЕ КРИТЕРИИ