Черт. 2.2. К примеру расчета 1
Требуется определить значение и точку приложения усилия предварительного обжатия Р(1) с учетом первых потерь и Р с учетом всех потерь для сечения в середине пролета, принимая максимально допустимое натяжение арматуры.
Расчет. Ввиду симметрии сечения расчет ведем для половины сечения плиты. Определяем геометрические характеристики приведенного сечения согласно п. 2.33, принимая 
:
площадь бетона A = 730·30 + 50·270 + 60·270/2 + 97,5·15 = 21900 + 13500 + 8100 + 1462,5 =
= 44962,5 мм2;
приведенная площадь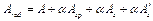 
= 44962,5 + 6,67·201 + 6,67·50,3·2 =
= 44962,5 + 1340,7 + 671 = 46974 мм2;
статический момент сечения бетона относительно нижней грани ребра
S = 21900·285 + 13500·135 + 8100·180 + 1462,5·48,7 = 9593200 мм3;
расстояние от центра тяжести приведенного сечения до нижней грани ребра
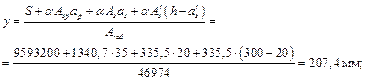
ysp = y - ap = 207,4 - 35 = 172,4 мм;
ys = y - as = 207,4 - 20 = 187,4 мм;
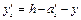= 300 - 20 - 207,4 = 72,6 мм;
момент инерции приведенного сечения
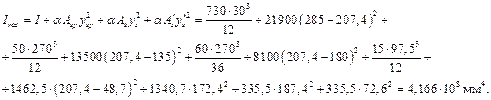
Согласно п. 2.25 максимально допустимое значение ssp без учета потерь равно
ssp = 0,9 Rs,n = 0,9 · 600 = 540 МПа.
Определим первые потери.
Потери от релаксации напряжений в арматуре согласно п. 2.27 равны
Dssp1 = 0,03 · ssp = 0,03 · 540 = 16 МПа.
По агрегатно-поточной технологии изделие при пропаривании нагревается вместе с формой и упорами, поэтому температурный перепад между ними равен нулю и, следовательно, Dssp2 =0.
Потери от деформации формы Dssp3 и анкеров Dssp4 при электротермическом натяжении арматуры равны нулю.
Таким образом, сумма первых потерь равна Dssp(1) = Dssp1 = 16 МПа, а усилие обжатия с учетом первых потерь равно
P(1) = Asp (Dssp - Dssp(1)) = 201 (540 - 16) = 105324 Н.
В связи с отсутствием в верхней зоне напрягаемой арматуры (т.е. при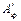 
= 0) из формулы (2.10) имеем
е0р1 = ysp = 172,4 мм.
В соответствии с п. 2.34 проверим максимальное сжимающее напряжение бетона sbp от действия усилия P(1) вычисляя sbp по формуле (2.8) при уs = y = 207,4 мм и принимая момент от собственного веса М равным нулю:
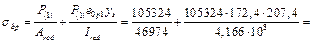
= 11,28 МПа < 0,9 Rbp = 0,9 · 17,5 = 15,75 МПа.
т.е. требование п. 2.34 выполняется.
Определяем вторые потери напряжений согласно пп. 2.31 и 2.32.
Потери от усадки равны Dssp5 = 0,0002 · 2 · 105 = 40 МПа.
Потери от ползучести определяем по формуле (2.7), принимая значения jb,cr и Еb по классу бетона В25 (поскольку Rbp = 0,7B), т.е. согласно табл. 2.6 jb,cr = 2,5, согласно табл. 2.5 Eb = 3·104 МПа; 
;
.
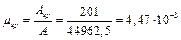Определим напряжение бетона на уровне арматуры S по формуле (2.8) при ys = ysp = 172,4 мм. Для этого определяем нагрузку от веса половины плиты (см. п. 2.12)
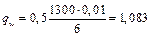кН/м.
и момент от этой нагрузке в середине пролета
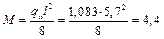кН·м (здесь l = 5,7 м – расстояние между прокладками при хранении плиты); тогда
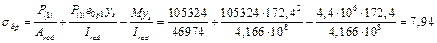МПа.
Напряжение бетона на уровне арматуры S' (т.е. при ys =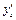 
= 72,6 мм)
МПа < 0,0.
Потери от ползучести
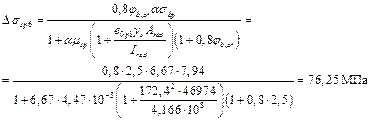
Вторые потери для арматуры S равны
Dssp(2) = Dssp5 + Dssp6 = 40 + 76,2 = 116,2 МПа.
Суммарная величина потерь напряжения
Dssp(1) + Dssp(2) = 16 + 116,2 = 132,2 МПа > 100 МПа,
следовательно, требование п. 2.36 выполнено и потери не увеличиваем.
Напряжение ssp2 с учетом всех потерь равно
ssp2 = 540 - 132,2 = 407,8 МПа.
Усилие обжатия с учетом всех потерь напряжений Р определяем по формуле (2.17). При этом сжимающее напряжение в ненапрягаемой арматуре ss условно принимаем равным вторым потерям напряжений, вычисленным для уровня расположения арматуры S, т.е. ss = ssp2 = 116,2 МПа, а поскольку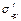 
< 0, напряжение 
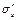принимаем равным нулю.
Р = ssp2 Asp - ss As = 407,8 · 201 - 116,2 · 50,3 = 76123 Н;
Эксцентриситет усилия Р равен
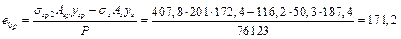мм.
Пример 2. Дано: свободно опертая балка с поперечным сечением по черт. 2.3; бетон класса В40 (Eb = 36000 МПа); передаточная прочность бетона Rbp = 20 МПа; напрягаемая арматура класса К1400 (Rs,n = 1400 МПа, Еs = 18·104 МПа) площадью сечения: в растянутой зоне Аsp = 1699 мм2 (12Æ15), в сжатой зоне 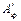= 283 мм2 (2Æ15); способ натяжения механический на упоры стенда; бетон подвергается пропариванию; длина стенда 20 м; масса балки 11,2 т; длина балки l = 18 м.
Требуется определить величину и точку приложения усилия предварительного обжатия с учетом первых потерь Р(1) и с учетом всех потерь Р для сечения в середине пролета, принимая максимально допустимое натяжение арматуры.
Расчет. Определяем геометрические характеристики приведенного сечения согласно п. 2.33, принимая коэффициент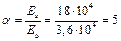 
(площадь сечения конструктивной ненапрягаемой арматуры не учитываем в виду ее малости).
Для упрощения расчета высоту свесов полок усредняем.
Площадь сечения бетона
А = 1500·80 + 280·240 + 200·250 = 120000 + 67200 + 50000 = 237200 мм2;
площадь приведенного сечения
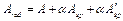= 237200 + 5·1699 + 5·283 = 237200 + 8495 + 1415 = 247110 мм2;
расстояние от центра тяжести сечения арматуры S до нижней грани балки (учитывая, что сечения всех четырех рядов арматуры одинаковой площади)
аp = (50 + 100 + 150 + 200) / 4 = 125 мм;
статический момент сечения бетона относительно нижней грани балки
S = 120000·750 + 67200·1380 + 50000·125 = 1,89·108 мм3;
расстояние от центра тяжести приведенного сечения до нижней грани балки
