Векторы и операции над ними.
Полем какой-либо величины называется пространство, в каждой точке которого эта величина вполне определена. Если эта величина скаляр, т.е. характеризуется одним числом, то поле называют скалярным (поле плотности, поле температуры).
Векторным называется поле, которое характеризуется в каждой точке пространства величиной и направлением. К этому следует лишь добавить, что непременным условием, связанным с векторными величинами, является то, что они должны складываться по правилу параллелограмма. Поэтому, например, поток автомашин, движущихся по улице и характеризующийся как величиной, так и направлением не является вектором.
Единичные векторы (орты) в декартовой системе координат будем обозначать 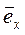 ,
, 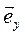 ,
, 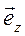 . Тогда вектор
. Тогда вектор 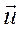 может быть представлен как
может быть представлен как
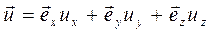 (1.2)
(1.2)
где 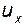 ,
, 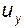 ,
,  - проекции (компоненты) вектора на соответствующие оси координат.
- проекции (компоненты) вектора на соответствующие оси координат.
Скалярное произведение двух векторовдает скалярную величину
 (1.3)
(1.3)
где - угол между векторами.
Ясно, что скалярное произведение обращается в нуль, если векторы  и
и  взаимно перпендикулярны.
взаимно перпендикулярны.