Мысал 1.56.
Контурлық тоқтар әдісі бойынша, 1,24 суреттегі тоқтарды анықтаңыз. Схеманың параметрлерін 1,2 есебінен аламыз.

Шығарылуы
1. Тәуелсіз контурларды анықтаймыз. Суретте көрсетілген 1 контур және 2 контур.
2. Тәуелсіз контурларды айналу бағытын қабылдаймыз (сур. 1.24). Контурлық тоқтар  және
және  бағыттары да сонда көрсетілген.
бағыттары да сонда көрсетілген.
3. Тоқ көзінің тоғы J , R4 және R5 кедергілері арқылы ағып өтеді, (1.24 суретінде пунктир).
4. 1-ші және 2-ші контурлар үшін Кирхгофтың екінші заңы бойынша теңдеулер құрастырамыз.
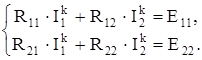
мұнда, R11 = R1 + R4 + R3 = 14 Ом;
R22 = R3 + R2 + R5 = 14 Ом;
R12 = R21 = R3 = 5 Ом;
E11 = E1 + E4 + E3 - J×R4 = 17 В;
E22 = E2 + E3 - E5 + J×R5 = 15 В.
5. Коэффициенттерді орындарына қойып теңдеулер жүйесінің шешуін табамыз. (1.19)

Анықтауышты есептейміз (1–20)
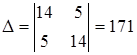 ; D11 = 14; D22 = 14; D12 = D12 = - 5;
; D11 = 14; D22 = 14; D12 = D12 = - 5;
 А;
А;
 А
А
6. Тармақтардағы тоқтарды есептейміз
 А;
А;
 А;
А;
 А;
А;
 А;
А;
 А.
А.
Электр тізбектерін есептеудің әртүрлі әдістерін салыстыру
Жоғарыда бір схеманың (рисур. 1.21) тоқтарын әр түрлі әдістермен есептеу көрсетілді. Осы әдістерді салыстырып көрейік. Берілген есепті шығару үшін 5 тармақтағы тоқтарды есептеу керек болды ол үшін: Кирхгоф заңдары бойынша - 5 теңдеуді, түйіндік потенциалдар әдісі бойынша – 3 теңдеу, ал контурлық тоқтар әдісі бойынша – 2 теңдеуді шешу керек болды№ Бұдан көріп отырғанымыз ең тиімдісі - контурлық тоқтар әдісі болып шықты.
Тұжырым: Әрбір схема үшін ең тиімді (рационалды) есептеу әдісі бар. Айта кету керек, электр тізбегін ықшамдау үшін энергия көзінің бір түрінен екінші түріне өтуді пайдалануға болады. Схеманың түрлендіру жасалмаған бөлігінде тоқтар өзгеріссіз қалатыны, сонымен қатар, тоқ көзі және ЭҚК көздерінің қуаттары әр түрлі болатыны айтылды. Осы жағдайды келесі есепте қарастырамыз
Мысал 1.7. Тоқ көздерін ЭҚК көздеріне түрлендіріп, . 1.21 суретіндегі схеманы есептеу керек. Түрлендірген схема үшін қуаттар балансын құрастырыңыз. Схема параметрлерін 1.3 есбінен алыңыз.
ШЫҒАРЫЛУЫ
- Тоқ көздерін ЭҚК көздеріне түрлендіру . 1.22 суретіндегі схемада көрсетілген.

. Айта кету керек, 2 –ші түйін үщін Кирхгофтың бірінші заңы бұзылмайды. Эквивалентті ЭҚК –ін есептейміз.
EЭ1 = R4×J = 4×2 = 8 В; EЭ2 = R5×J = 5×2 = 10 В.
2. Бұл ЭҚК-ің қосылуы және оларды есептеуге арналған схема 1.23. суретінде көрсетілген.
3. 1.23.суретіндегі схеманы есептеуге арналған әдісті таңдаймыз.
Кирхгоф заңдары бойынша - 3 теңдеуді, ал контурлық тоқтар әдісі бойынша – 2 теңдеуді түйіндік потенциалдар әдісі бойынша – 1 теңдеуді шешу керек болды(себебі схемада 2 түйін бар, олардың біреуінің потенцалы нольге тең, яғни жермен жалғаймыз, сонда  = 0.)
= 0.)
Сонымен ( 1.16) бойынша :  g22=
g22= 

Мәндерін қойып есептейміз
 В.
В.

. 1.23 суретіндегі схеманың тоқтары:
 А;
А;
 А;
А;
 А.
А.
1.21 суретіндегі схеманың тоқтарын Кирхгофтың бірінші заңын пайдаланып анықтаймыз.
I4 = I1 + J = 0,95 + 2 = 2,95 А;
I5 = J - I2 = 2 - 0,73 = 1,27 А.
Бұл есепті шығаруда кең таралған екі түйін формуласын пайдаландық.

Жалпы алғанда тармақтар саны кез келген болуы мүмкін және 0 және 2 түйіндері арасында жалғанған тармақтарда тоқ көздері де болуы мүмкін, сондықтан жалпы түрде формуланы келесі түрде жазамыз.
 (1.21)
(1.21)
(1.21) формуласын кейін де біз көп қолданатын боламыз
4. Түрлендірген схема үшін қуаттар балансын құрастырамыз
 ;
;
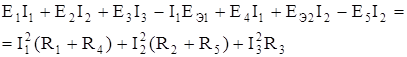
Мәндерін орындарына қойып табамыз::
10×0,95 + 15×0,73 + 10×1,68 - 8×0,95 + 5×0,95 + 10×0,73 - 20×0,73 =
= (0,95)2×9 + (0,73)2×9 + (1,68)2×5;
27,1 Вт = 27,1 Вт.
1.4 есебінің шешуімен салыстырыңыз..
Қабаттасу принципі және әдісі
Мысал 1.8. 1.26 суртеіндегі схеманың келесі параметрлері берілген: 
R2 = 12 Ом; R5 = 20 Ом; E3 = 50 В; R3 = 10 Ом; J1 = 2 А; R4 = 40 Ом; E2 = 20 В.
Кіріс және өзара өткізгіштіктер мен беріліс коэффициенттерін (тоқ бойынша) анықтаңыз. I2, I3, I4, I5 тоқтарын анықтайтын теңдеулерді жазыңыз.

1. Тек қана J1 тоқ көзінің әсер еткендегі схеманы есептейміз (сур. 1.27).
Құраушы тоқтардың бағытын бастапқы схемадағыдай (сур. 1.26.)сақтаймыз.
 Ом; R5 = 20 Ом.
Ом; R5 = 20 Ом.
Бұдан, құраушы тоқтар:






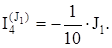
Беріліс коэффициенттерін (тоқ бойынша) анықтаймыз:



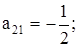
Аналогия бойынша,



.
1. Тек қана E2 көзінің әсер еткендегі схеманы есептейміз (сур. 1.28) :
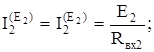
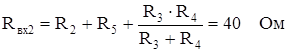 ;
;

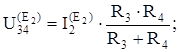
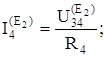


Кіріс және өзара өткізгіштіктерді анықтаймыз:
 См; или
См; или  См;
См;
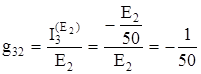 См.
См.
Аналогия бойынша,
 См;
См;  См.
См.
1. Тек қана Е3 көзінің әсер еткендегі схеманы есептейміз (сур. 1.29) :

 Ом;
Ом;  ;
;
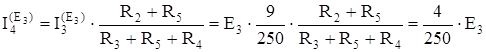 ;
;
 .
.
Кіріс және өзара өткізгіштіктерді анықтаймыз:
 См;
См;  См.
См.
Аналогия бойынша,
 См;
См;  См.
См.
4. I2, I3, I4, I5. тоқтарын анықтайтын теңдеулерді жазыңыз




Мысал 1.9. 1.8 есебінің шешімін қолданып I4 және I5 тоқтарын есептеңіз.
ШЫҒАРЫЛУЫ
 А;
А;
 А.
А.
Мысал 1.10. 1.8 есебінің шартында Е2 –нің келесі мәндері үшін: а) 40 В; б) 80 В. I4 және I5.тоқтарын есептеңіз
ШЫҒАРЫЛУЫ
а)Е2=40В; А;
А;
 А.
А.
а) Е2 = 80 В;  А;
А;
 А.
А.
1.1. Өзаралық принципі
Кез келген сызықты тізбектің n тармағына En ЭҚК –ін қосу салдарынан пайда болған k тармағындағы Ik тоғы, k тармағына Ek = En ЭҚК –ін қосу салдарынан пайда болған n тармағындағы In тоғына тең болады.
Қарастырып отырған тізбекте алдымен ЭҚК тек қана n - тармағында әсер етсін, содан кейін k-тармағыныда әсер етсін және Ek = En. Тізбекте басқа ЭҚК жоқ
контурлық тоқтар әдісі бойынша:


Dkn = D nk сондықтан 
Бұл өзаралық принциптің дәлелі болып табылады.
1.8 есебінде көрсетуге болады.
Е2 ЭҚК –і әсер еткенде: 
Е3 ЭҚК –і әсер еткенде:
Егер Е2 = Е3 болса,  .
.
Өзаралық принципінің келесі маңызды теңдеуін аламыз:
g23 = g32
немесе, gkn = gnk. (1.23)


1.25 және 1.30 суреттерінде өзаралық өткізгіштіктерді Эксперименталды анықтауы көрсетілген.
1.12. Компенсация (теңестіру)туралы теорема
«Электр тізбегінде кез келген тоқ өтіп жатқан кедергіні, мәне осы кедргідегі кернеудің түсуіне тең ЭҚК-мен алмастыруға болады. Бұл ЭҚК-ың бағыты осы кедргідегі тоқтың бағытына қарсы болуы керек».

Бұл теореманы дәлелдеу үшін 1.31 а, б, в. Суреттерін қарастырамыз. R кедргісіндегі кернеудің түсуі U = R×I (сур. 1.31 а). Кедергіге тізбектей екі ЭҚК -ін қосамыз, олардың мәні R,кедергісіндегі кернеудің түсуінің мәніне тең (яғни, R×I) және бағыттары қарама-қарсы. Бұл жағдайда схемадағы тоқтардың мәндері өзгермейді. «а» және «d» нүктелері арасындағы тізбек бөлігінде потенциалдың өзгеруін қарастырамыз. «а» нүктесінің потенциалын белгілі деп есептеп, «d» нүктесінің потенциалын табамыз:

«а» және «d» нүктелерінің потенциалдары бір-біріне тең болғандықтан, осы екі нүктені бір-ьбірімен қосып қысқа тұйықтаймыз. 1.31 б суртеіндегі схема 1.31 в суртеіндегі схемаға ауысады.
1.1. Сызықтық электр тізбектеріндегі сызықтық қатынастар.
Егер сызықтық электр тізбегінде кез келген бір тармақтың кедергісі немесе ЭҚК өзгерсе, кез келген екі тармақтардағы екі тоқ(немесе, осы тармақтардағы элементіндегі кернеудің түсуі) бір-бірімен келесі қатынаспен байланысқан:

Осыны дәлелдейік. Қабаттасу принципі бойынша:


Схемада тек қана Еm ЭҚК-і өзгерсін. Сонда,


Екінші теңдеуден

Бұл теңдеуді бірінші теңдеуге қоямыз.

Бұдан
 (1.24)
(1.24)
а және b коэффициенттерін эксперименталды немесе есептеу жолымен екі режим бойынша анықтаймыз.
Мысал 1.11. 1.10 есебінің шешуін пайдаланып,  сызықтық қатынасының коэффициенттерін анықтаңыз.
сызықтық қатынасының коэффициенттерін анықтаңыз.
ШЫҒАРЫЛУЫ
Егер, E2 = 40 В болса, онда I4 = 0,8 А; I5 = 1 A.
Егер E2 = 60 В болса, онда: I4 = 1,0 А; I5 = 2 A.
Екі теңдеу құрамыз
 бұдан
бұдан 
Сонымен,

Тексеру. 1.8 мысалында Е2 = 20 В болғанда, I4 = 0,7 А және I5 = 0,5 A тең болды. Бұл алдындағы теңдеуді қанағаттандырады.
0,7 = 0,6+0,2×0,5; 0,7 А = 0,7 А.

Өз бетімен шығаруға арналған есептер (1-ші тақырып үшін)
1. 1.32 суретіндегі схема үшін контурлық тоқтар, түйіндік потенциалдар және қабаттасу әдісі бойынша тоқтарды анықтаңыздар.
Жауаптары: I1 = 2 А; I2 = 5 А; I3 = 15 А.
2. 1.32 суретіндегі схеманың тармақтары үшін өзіндік және өзара өткізгіштіктерді және тоқ бойынша беріліс коэффициентін анықтаймыз:
Жауаптары: g11 = 0,4 См; g22 = 0,15 См; g33 = 0,345 См;
g12 = g21 = 0,1 См; g31 = g13 = 0,3 См,
 ;
;  ;
;  .
.
3. 1.32 суретіндегі схема үшін I2 және I3.тоқтарының арасындағы сызықтық қатынасты анықтаңыз.
Жауаптары: I2 = 0,05 + 0,033×I3.
Мысал 2.1. 2.4 а. суретіндегі схема үшін: R1 = 5,2 Ом; R2 = 8 Ом; R3 = 4 Ом; R4 = 10 Ом; R5 = 40 Ом; Е1 = 100 В.

Ықшамдау арқылы I1 тоғын анықтаңыз
ШЫҒАРЫЛУЫ
Параллель жалғанған R4 және R5, кедергілеріне эквивалентті кедргісін табамыз
 Ом (рис. 2.4 б).
Ом (рис. 2.4 б).
Одан әрі тізбектей жалғанған R3 және R6 кедергілерін келесі кедергіге ауыстырамыз:
R7 = R3 + R6 = 12 Ом (рис. 2.4, в).
Параллель жалғанған R2 және R7, кедергілеріне эквивалентті кедргісін табамыз
 Ом (сур. 2.4 г).
Ом (сур. 2.4 г).
Енді схемада тек қана бір контур бар, оған Кирхгофтың екінші заңы бойынша теңдеуді оңай құрастыруға болады
 , бұдан,
, бұдан,  А.
А.

2.3. Пассивті кедергілер үшбұрышын жұлдызшаға немесе керісінше түрлендіру
Мысал 2.2. 2.6 а суретіндегі схема үшін:
R1 = 2 Ом; R2 = 4 Ом; R3 = 2 Ом; R4 = 5 Ом; R5 = 3 Ом; R6 = 6 Ом; Е1 = 12 В; Е2 = 10 В.
Тармақтардағы тоқтарды анықтаңыз.

ШЫҒАРЫЛУЫ
Егер есепті шығарғанда схеманы алдын ала түрлендірмесек,Кирхгоф заңдары бойынша - 6 теңдеуді, түйіндік потенциалдар әдісі бойынша – 3 теңдеу, 6 контурлық тоқтар әдісі бойынша – 3 теңдеуді шешу керек болады.

R3, R4, R5 кедергілер үшбұрышын эквивалентті жұлдызшаға түрлендіреміз№ Сонда схема келесі түрде болады: сур. 2.6 б.
Бұл схема үшін, (2.6), (2.7) және (2.8) бойынша,
 Ом;
Ом;
 Ом;
Ом;
 Ом.
Ом.
I1, I2 және I6 тоқтары 2.6 а и 2.6 б.32 суреттеріндегі схема үшін өзгеріссіз қалады, себебі олар түрлендіруге қатыспаған схеманың бөлігінде орналасқан тармақтарда өтіп жатыр. Тізбектей қосылған кедергілерді эквивалентті кедергіге ауыстырып табамыз:
 Ом;
Ом;  Ом;
Ом;  Ом.
Ом.
2.6 б суретіндегі схема 2.6 а. суретіндегі схемаға айналады.

2.6 в суретіндегі схемада екі түйін бар, бұл түйіндік потенциалдар әдісі бойынша бір ғана теңдеуді жазуға болады. Ол үшін, j4 = 0, деп алып, «екі түйін» формуласын қолданамыз 1.21)
 В.(2.9)
В.(2.9)
Одан әрі, жалпы түрдегі Ом заңын қолданып, схеманың түрлендірмеген бөлігіндегі(j 4 = 0) I1, I2 және I6 тоқтарын табамыз
 А;
А;  А;
А;  А.
А.
I3, I4 и I5 тоқтарын табу үшін 2.6 б суретіндегі схемаға ораламып, 1, 2, 3 –ші түйіндердің потенциалдарын анықтаймыз (j 4 = 0).
 В;
В;  В;
В;  В.
В.
Эквиваленттілік шарттары бойынша, 12.6 а суретіндегі схеманың 1,2,3-ші түйіндерінің потенциалдары және 12.6 б суретіндегі схеманың 1,2,3-ші түйіндерінің потенциалдары бірдей. Сондықтан, 2.6 ба суретіндегі схеманың I3, I4, I5 тоқтары үшін:
 А;
А;  А;
А;  А.
А.
2.4. ЭҚК-і және тоқ көздері бар параллель тармақтары бар схеманы түрлендіру
Мысал 2.3.. 2.7 а суретіндегі схеманы 2.7 б суретіндегі схемаға түрлендіріңіз, егер R1 = R2 = R3 = R4 = 60 Ом; Е1 = 90 В; Е2 = 30 В; J3 = 1 А.

ШЫҒАРЫЛУЫ
1. Тармақтардың өткізгіштігін анықтаймыз 
 ;
;  .
.
2. Эквивалентті энергия көзінің өткізгіштігін анықтаймыз

 ;
;  Ом.
Ом.
3. Тоқ көзінің тоғын анықтаймыз
 А,
А,
Мұнда, J1 және J2 – эквивалентті энергия көздері.
4. Түрлендірген схеманы құрастырамыз (2.7 б суретіндегі схема ).
Эквивалентті генератор әдісі
Мысал 2.4. 2.6 суретіндегі схемада I2 тоғын эквивалентті генератор әдісімен анықтаңыз. Схеманың параметрлерін 2.2 мысалынан алыңыз.
ШЫҒАРЫЛУЫ
1. 2-4 қысқыштарына қатысты эквивалентті генератор параметрлерін анықтаймыз. 2.12 а суретінде екінші тармағы ажыратылған(Е2, R2) схема көрсетілген.
2.12 а суретіндегі эквивалентті генератордың параметрлері: 4,2 қысқыштары арасындағы бос жүріс кернеуі - U42Х және RВ42 – 4,2 қысқыштарына қатысты кіріс кедергісі. Айта кету керек, 2.12 а суретіндегі схеманың тоқтары 2.6. суретіндегі тоқтарға тең емес.
2. Алдымен кіріс кедергісін анықтаймыз. Ол үшін, Е1 ЭҚк-ін шығарып тастаймыз (қысқа тұйықтаймыз) ішкі кедергісін қалдырамыз, бірақ бұл мысалда ол нольге тең.). Пайда болған схемада (рис. 2.12 б) R3, R4 және R5 кедергілер үшбұрышын эквивалентті жұлдызшаға түрлендіріп, 2.12 а. суретіндегі схеманы аламыз.
rа, rб, rв мәндері 2.2. мысалынан алынады. Содан кейін, түрлендіру жасаймыз.

 Ом;
Ом;  Ом;
Ом;  Ом.
Ом.
Ақырында,

 Ом.
Ом.
3. UХ бос жүріс кернеуі н. 2.12 г схемасынан анықтаймыз . Бұл схемада бір ғана контур, оның тоғы:
 А.
А.
rб кедергісімен тоқ жүрмеейді, сондықтан,  В.
В.

4. 2.12 г суретіндегі схеманы, 2–4 қысқыштарынан сол жағын эквивалентті схемаға түрлендіреміз (сур. 2.12 б). 2–4 қысқыштарына екінші тармақты (Е2, I2) жалғап, I2тоғын анықтаймыз.
 А.
А.
Өз бетімен шығаруға арналған есептер (2-ші тақырып үшін)

2.13 суретіндегі схемада амперметрдің көрсеткішін табыңыз(амперметрдің ішкі кедергісін нольге тең деп аламыз):
а) схеманы түрлендіру арқылы;
б) эквивалентті генератор әдісімен.
Жауабы: IА = 1 А.

2.14 суретіндегі схема үшін берілгені:
r1 = 120 0м; r2 = 180 Ом; r3 = 120 0м;
r4 = 80 Ом; r5 = 80 Ом; r6 = 50 Ом; E = 12 В.
Көпірдің диагоналіндегі тоқт анықтаңыз.
Жауабы: I = –0,0084 А.