Бриллюэн зонасы

 

Тура тордың периоды a болсын делік. Кері тор ұғымы периодты функцияның жазық толқындарға үлестірілуінен туындады. Бірөлшемді жағдайда периодты функцияның Фурье қатарына үлестірілуі мына түрде болады:

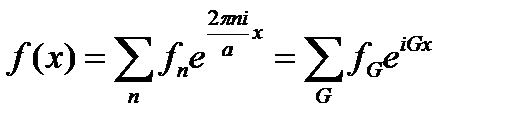(1.1)

Осылайша, бірқалыпты жағдайда кері торды G_n=2πn/a нүктелері құрады, бұл нүктелер кері тордың векторларының рөлін атқарады. Жеңіл болу үшін біріншіден, бірөлшемді торды және бірөлшемді Бриллюэн зонасының құрылуын қарастырамыз. Бриллюэн зоналары келесі түрде құрылады: кері торда түйіндерді қосатын кесінділердің ортасына нүкте қойылады. Бірінші зона — [–π/a,π/a] кесіндісі, екіншісі — бірінші зонаны алып тастандағы [–2π/a,2π/a] кесіндісі, және т.с.с. (18-сурет)

1.20-сурет. Бірөлшемді жағдайдағыБриллюэн зонасы.

1.21-суретте екіөлшемді тікбұрышты кері тор үшін Бриллюэннің төрт зонасы бейнеленген. Олар бірөлшемді жағдайдағыдай құрылады, тек нүктелердің орнына түзу сызықтар жүргізіледі.

Үшөлшемді тор үшін Бриллюэн зонасы ослай құрылады тек түзулердің орнына жазықтықтар жүргізіледі. Осылай анықталған жазықтықтар класы, координаталар басымен қосылған кері тордың түйіндерінің жан-жағын көпжақты пішіні бар қандай да бір көлеммен шектейді. Қарапайым кубты тор жағдайында көпжақты куб болып табылады. Оның қырлары осы тордың түйіндерін басқа көрші түйіндерімен қосатын векторлардың ортасы арқылы өткізілетін жазықтармен құрылған. Барлық басқа жазықтар түйіннен алшақ өтеді және кубтың қырларының құрылуына өз үлесін қоспайды. Көлемді-центрленген кубты тор жағдайында күрделі көпжақтылар құрылады (төменді қара). Оның қырлары берілген түйін мен оның жақын бірінші және екінші көршілері арасынан өткізілген жазықтармен құрылады. Құрылған көпжақтылар Бриллюэннің бірінші зонасыдеп аталады. Егер барлық жазықтардың бірігуінен Бриллюэннің бірінші зонасының қырларын алып тастасақ, онда қалған көптік координата басы айналасында жаңа көпжақтының құрылуын шектейді. Бриллюеннің бірінші зонасына кірмейтін осы көптіктің жартысы Бриллюэннің екінші зонасын түзеді. Келесі қадамда біз Бриллюэннің үшінші зонасын аламыз және т.с.с.

 

1.21-сурет

Бриллюэннің бірінші зонасын нүктелік симметриясы бар, кері тордың примитивті ұяшығы ретінде қарастыруға болады. Расында да, егер кері тордың әр түйінінің жанына Бриллюэннің бірінші зонасын құрсақ (координаталар басын осы түйінге орналастырсақ), онда осы зоналар бір-бірімен беттеспей барлық кеңістікті толығымен толтырады. Мұнда Бриллюэннің бірінші зонасының көлемі кері тордың примитивті ұяшығының көлеміне тең болатындығын көруге болады.

Бриллюэннің кейбір қасиеттері:

Бриллюэннің барлық зоналарының көлемдері бірдей және кері тордың примитивті ұяшығының көлеміне тең.

Бриллюэннің барлық зоналары бірінші зонаның репликасы болып табылады: оларды бірінші зонаға жататын нүктелерін кері тор векторына трансляциялау арқылы алуға болады.

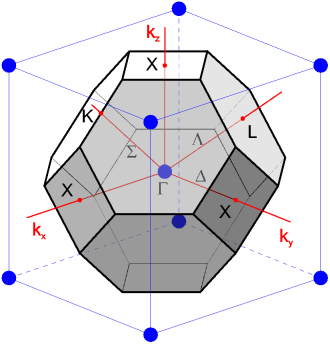
1.22-сурет

 

Жартылайөткізгіштердің кең таралған түрлерінің көпшілігінің торлары қырға центрленген кубты (ГЦК) Браве торларына жатады, осы тордың Бриллюэннің бірінші зонасы қалай орналасқанын қарастырайық. Мұндай жағдайда кері тор көлемді центрлі кубты (КЦК) болып табылады. Бриллюэннің бірінші зонасы 1.22-суретте бейнеленген. Жоғарыда көрсетілген алгоритмге сәйкес ол келесідей болады. Бірінші кубты, қарапайым ұяшықтың центріндегі түйін мен оның екінші көршісінің арасын қосатын түзуді екіге бөлетін жазықтық жүргіземіз. Бұл жазықтықтар кубты ұяшықтармен сәйкес келетін, орталық түйіннің жан жағындағы кубты шектейді. Осы кубтың бұрыштарында орталық түйіннің жақын көршілері орналасқан. Осы көршілері мен орталық түйіндері арасынан жүргізілетін жазықтықтар кубпен қиылысқан кезде алтыбұрышты қырларды түзеді, ал кубтың қырларынан квадраттарды ''қиып '' алады.

ГЦК-торда Бриллюэннің бірінші зонасының кейбір жоғары симметриялы нүктелері мен сызықтарының жалпыға бірдей белгіленулері бар. Бриллюэн зонасының центрі грек әрпімен белгіленеді Γ. Жазықтық бетіндегі нүктелер латын әріптерімен белгіленеді: X — квадрат қырының центрі (k-жазықтығындағы (1,0,0) бағыты және оған эквивалент барлығы 6 нүкте); L — алтыбұрышты қырдың центрі ((1,1,1) бағыты және оған эквивалент барлығы 8 нүкте); K — көрші алтыбұрышты қырлардың арасындағы қабырғалардың ортасы ((1,1,0) бағыты және оған эквивалент барлығы 12 нүкте). Зона центрі мен жазықтық бетіндегі нүктелерді қосатын сызықтар грек әріптерімен белгіленеді: Γ X — Δ ((1,0,0) түріндегі бағыт), ΓL — Λ ((1,1,1) түріндегі бағыт), Γ K - Σ ((1,1,0) түріндегі бағыт).

 

2. Бөлім. Толқындардың конденсирленген ортамен әсерлесуі

2.1. Кристалдардың құрылымын зерттеу үшін қолданылатын электромагнитті толқындар

Кейбір кристалды үлгілердің сыртқы симметриясы жөнінде ақпаратты макроскопиялық және микроскопиялық зерттеулердің көмегімен алуға болады. Дегенмен, көрінетін және ультракүлгін сәулеленудің ( 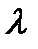~ 5000 —1000 А) рұқсат ету қабілеттілігі кристалдағы молекулалар мен атомдардың кеңістікте орналасуы мен олардың арасындағы қашықтығын анықтау үшін айтарлықтай жеткіліксіз, өйткені бұл арақашықтық шамасы бірнеше ангстремді құрайды (10 ^-10м).

return false">ссылка скрыта

Қандай да бір объектінің құрылымын микроскоп астында зерттеу, жалпы жағдайда, толқын ұзындығы төмендегі теңсіздікпен анықталатын, арақашықтан кем болатын сәулеленуді пайдалануды болжайды:

 

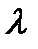_зерт< d_өлш (2.1)

 

Бұл жағдайда геометриялық оптика заңдарын қолдануға болады. (2.1) шартын қанағаттандыратын сәулеленудің толқын ұзындығы жоғары энергиялы қатты 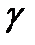-сәулеленуге, 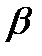- сәулеленуге сәйкес келеді. Дегенімен, қатты гамма -сәулеленудің затпен әлсіз әсерлесуінің салдарынан оны қолдану қиындықтарды тудырады. 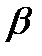- сәулеленудің (электрондар) керісінше, үшөлшемді кристалдың құрылуын талдау үшін өтімділік қасиеті жеткіліксіз. Оған қарамастан, белгілі құрылымы бар кейбір кристалдардың бетіндегі жазық атомдық торлардың микроскопиялық бейнесін алуға мүмкіндік беретін, жоғары рұқсат етілген электронды микроскоп бар.

Соңғы жылдары сканерлеуші туннелді микроскоптар (СТМ) мен атомдық күштік микроскоптардың (АКМ) мүмкіндіктерімен байланысты микроқұрылымдық зерттеулердің жаңа әдістері пайда болды.

Дегенмен, қазіргі уақытта кристалдық құрылымды зерттеудің дифракциялық әдістері өте жақсы дамыған, онда атомдық жазықтармен әсерлесетін диффракциялық толқындарды қолданады. Осы толқындардың ұзындығының шамасы кристалдағы атом арасындағы қашықтық шамасымен салыстырмалы болуы керек:

 

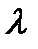_зерт ~ d_hkl(2.2)

 

Фотондар, нейтрондар мен электрондардың дифракциясын қолдану арқылы да кристалдың құрылымын зерттейді. Осы әдістер арқылы қарапайым ұяшықтың өлшемін, ядролардың орналасуын, ұяшықтағы электрондардың үлестірілуін анықтауға болады. Дифракцияланған толқынның сырғу бұрышы қристалдың құрылымы мен түсетін сәуленің толқын ұзындығына тәуелді.

Рентгендік сәулелер. Рентгендік сәулелердің квантының энергиясын мына қатынасқа сәйкес анықтауға болады:

Е _рент=hν=hc/λ (2.3)

 

мұндағы h = 6,62x10 ^-34 Дж∙с — Планк тұрақтысы, v және — сәуленің жиілігі мен толқын ұзындығы, с — вакуумдағы жарық жылдамдығы. Практикалық мақсат үшін бұл теңдеуді мына түрде жазу ыңғайлы:

 

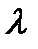(Å) = 12,4/Е(кэВ) (2.4)

 

Осыдан 1Å толқын ұзындығына Е ~ 12 кэВ энергия сәйкес келетіндігін көруге болады. Сондықтан кристалдарды зерттеу үшін квант энергиясы 10-50кэВ болатын рентгендік сәулелену қажет. Мұндай сәулеленуді екі механизм арқылы алуға болады:

1) металды нысанадағы жылдам электрондарды тежеумен (тежегіш сәулелену). Тежеу барысында, электродинамика заңдылығына сәйкес, қозған бөлшек электромагнитті сәуле шығару керек. Бұл сәулеленудің спектрі бірқалыпты кең спектр болады;

2) жылдам электрондар мен нысана атомдарының ішкі электрондарымен серпімсіз соқтығысуы (сипаттамалық сәулелену). Бұл сәулеленудің спектрі атом электрондарының жоғары энергиялы қозуларымен байланысты сызықты спектр болады. Нәтижесінде сәулеленудің спектрі жіңішке сызық болады. Түрлі металлды нысаналарды қолдана отырып монохроматты рентгендік сәулеленудің түрлі толқын ұзындықтарын алуға болады.

Нейтрондар.Бөлшектердің кинетикалық энергиясы және импульсі мына теңдеумен байланысты:

 

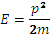(2.5)

Ал толқын ұзындығы мен импульс – мына теңдеумен:

 

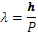(2.6)

Сонда нейтрон үшін де-Бройль толқын ұзындығы мен оның энергиясы мына қатынаспен байланысты болады:

 

(2.7)

Мұндағы m_n = 1,675х10^-27 кг - нейтронның массасы. Практикалық мақсат үшін осы теңдеуді мына түрде жазған ыңғайлы:

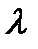_n(Å) = 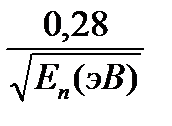(2.8)

Сәйкесінше, 1Å толқын ұзындығына Е_n = 0,08 эВ энергиясы сәйкес келеді, ал нейтрондар осындай энергиямен 4000 м/с жылдамдықпен қозғалады. Нейтрондар заттармен бірнеше әдіс арқылы өзара әсерлеседі:

1) магниттелмейтін кристалдарда нейтрондар атомдардың тек ядроларымен әсерлеседі, өйткені нейтронның заряды жоқ ал оның массасы атом бұлтшасының электрондарының массасынан әлдеқайда көп. Егер осы жағдайда серпімді, когерентті шашырау болса, онда дифракцияны байқауға болады. Нейтрондар мен рентгенді сәуленің дифракциялық суреттері бірдей;

2) нейтрондардың магниттік моменттерінің болуының арқасында олар магнитті кристаллдардың – ферро-, ферри-, антиферро-, парамагнетиктердің электрондарының магнитті моменттерімен өзара әсерлеседі, ол арқылы кристаллдардың магниттік қасиеттері жөнінде ақпарат алуға болады;

3) баяу нейтрондар тордың тербелісіне кететін серпімсіз шашырау процесіне қатысады, ол осындай тербелістерді зерттеуге мүмкіндік береді.

Электрондар.Де-Бройль толқын ұзындығы мына теңдеумен анықталады:

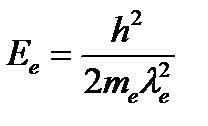(2.9)

Мұндағы m_e = 0,911х10^-30кг –электронның массасы. Практикалық мақсат үшін мына теңдеу ыңғайлы:

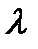_е(Å) = 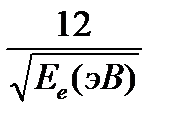(2.10)

1 Å толқын ұзындығына Е_е = 150 эВ энергиясы сәйкес келеді, ал электрондардың жылдамдықтары шамамен 7∙10⁶м/с. Өйткені электрон – зарядталған бөлшек, ол затпен өте жақсы әсерлеседі және серпімді және серпімсіз шашырауға келмей тұрып ол кристаллға бірнеше ангстремге еніп кете алады. Сондықтан көлемді кристаллдың құрылымы сәулелену үшін электрондардың дифракциясы жарамсыз болып қалады. Электронография әдетте кристаллдардың жазықтықты қабаттарын, беттерінің жағдайын, жұқа қабыршықты зерттеу кезінде қолданылады.

 

2.2. Кристалдық торға түсетін рентгендік сәулелердің дифракциясы

Кристалдардың атомдық құрылымы рентгендік сәуленің, электрондардың, нейтрондардың шашырауы және дифракциясымен анықталады. Рентгендік сәуле үшін үшөлшемді құрылымы бар кристалдар қарапайым табиғи дифракциялық тор болып табылады, өйткені рентгендік сәуленің толқын ұзындығының мәні кристалдағы ретпен орналасқан атомдар арасындағы қашықтық мәнімен шамалас, осы қорытындыны 1912 жылы неміс физигі М. Лауэ жасаған.

Кристалды тордан рентгендік сәуленің дифракциясын есептеудің қарапайым әдісін бір-біріне тәуелсіз кеңес одағының физигі Г.В. Вульф пен ағылшын физиктері Г. және Л. Брэггтер ұсынған. Олардың пайымдауынша, рентгендік сәуленің дифракциясы кристалдық торлардың түйіндері (атомдары) жататын параллель кристаллографиялық жазықтықтар жүйесінен (2.1-сурет) сәуленің шағылуының нәтижесі болып табылады.

Кристалды бірінен-бірі d арақашықтықта орналасқан, параллель кристаллографиялық жазықтықтар жиынтығынан тұрады деп есептейік. Параллель монохроматты рентгендік сәуле ағыны (1,2) сырғу бұрышын (кристаллографиялық жазықтық пен түсетін сәуле бағытының арасындағы бұрышы) жасайды және бір-бірімен интерференцияланатын, 1^/ және 2^/ когерентті қосымша толқындардың шоғыры болып табылатын, кристалдық тор атомдарын қоздырады.

 

 

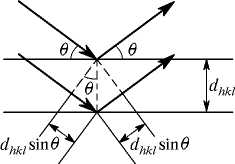
2.1-сурет -Рентгендік сәуленің кристаллографиялық жазықтықтан шағылысуы

 

Дифракциялық максимумдар атомдық жазықтықтан шағылысқан барлық толқындар бір фазада болатын бағыттарда байқалады. Бұл бағыттар Вульф-Брэгг теңдеуін қанағаттандырады:

2d_hkl sin 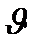= m 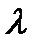(m=1,2,3,…) (2.11)

Яғни, дифракциялық максимум толқын ұзындығының 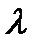бүтін санына тең көрші кристаллографиялық жазықтықтан шағылысатын екі сәуленің арасындағы жол айырымына тең.

Рентгенді құрылымды талдау әдісі түсіру шартына байланысты екі түрге бөлінеді: а) сәуленің кристаллға түсу бұрышы тұрақты, бірақ толқын ұзындығы өзгереді; б) толқын ұзындығы тұрақты, ал түсу бұрышы өзгереді. Екі жағдайда фотопластинкаға, пленкаға немесе есептегішке Вульф-Брэггтер шартына жауап беретін дифракциялық максимумдер тіркеледі.

а) түріндегі әдіске Лауэ әдісі жатады, ал б) түріндегі әдіске айналу әдісі Дебай-Шерер әдісі жатады. Осы әдістерді толығырақ қарастырып өтейік.

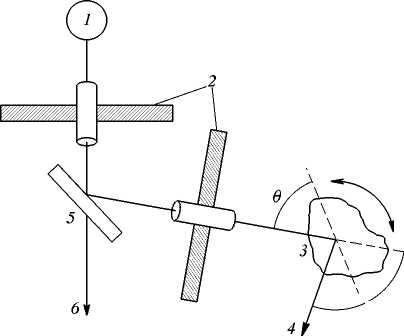
Лауэ әдісі.Рентген сәулесін жіңішке ағыны төмендегі 2.2-суретте көрсетілгендей монокристалға түседі. Монохроматты емес рентгендік сәуленің немесе нейтрондардың ағыны шоғырдан 1 коллиматор арқылы 6 өлшемі 1мм-ден аспайтынмонокристалды үлгіге 2 түседі.

2.2-сурет - Лауэ әдісін түсіндіру үшін

 

Осы шоғыр арқылы сәулелену толқын ұзындығы кең диапазонды қамтиды, және (2.11) шартын қанағаттандыратын қандай да бір толқын ұзындығы үшін дифракциялық рефлекс туындайды. Шын мәнінде, кристалл дифракциялық шағылысудың дискретті жиынтығын таңдап алады. 2.2-суретте, үлестірілуі кристаллдың құрылымын және орналасу бағытын сипаттайтын, тура және кері дифракциялық «дақтар» жиынтығын түсіру үшін жазық фотопластинка немесе фотопленканың екі жағдайы 3 және 5 көрсетілген. Алынатын дифракциялық сурет кристалдың симметриясына сәйкес келеді: егер кристалл, мысалы, 4-ші ретті симметрия өсіне ие болса, осы өс түсетін шоғырға параллель болатындай бағытталса, онда лауэграммада 4-ші ретті симметрия өсіне ие болады.

Егер кристалдың құрылымы алдын ала белгісіз болса, онда дифракциялық дақтар жиынтығын ашып көрсету қиын болады, өйткені бірдей параллель жазықтық сериясынан фотопластинканың бір нүктесіне түсетін дифракция кезінде ұзындығы түрлі болатын толқындар шағылысуы мүмкін және оларға түрлі дифракциялық максимумдер сәйкес келеді. Сондықтан да жаңа құрылымдарды зерттеу үшін Лауэ әдісін жиі қолданбайды. Ол ең бірінші, симметрияны жылдам анықтау үшін немесе құрылымы белгілі кристалдың орналасу бағытын анықтау үшін қолданылады. Соңғы жағдайда үлгінің кеңістікте орналасуын үш өсті гониометр арқылы өзгертуге болады. Лауэ әдісін, кристалды термиялық және механикалық өңдеуден өткізген кезде пайда болатын ақаулар мен ауытқуларды анықтау үшін де қолданады.

Кристалдың айналу әдісі. Монокристалл рентгенді сәуленің немесе нейтронның монохроматты шоғырында қандай да бір өс арқылы айналады (2.3-сурет).

 

2.3-сурет - Кристалдың айналу әдісінің сызбасы: 1 — сәуле шығаратын шоғыр; 2 — коллиматорлар; 3— үлгі; 4 — фотопластинкаға немесе есептегішке бағытталған дифракцияланатын шоғыр; 5— кристалл-монохроматор; 6— ауытқымаған шоғыр.

 

1 шоғыр көзінен түсетін шоғырдың монохроматталуы кристалл-монохроматор 5 немесе фильтрлер арқылы жүзеге асады. Коллиматор 2 арқылыөтетін монохроматты шоғыр, үлгінің айналу барысында 9 бұрыш (2.11) шартын қанағаттандыратын барлық уақытта да монокристаллды үлгінің нақты бір атомдық жазықтығында дифракцияланады. Дифракциялық рефлекстер сериясы цилиндрге оралған фотопленкаға тіркеледі. Шоғырдан шыққан, жазықтардан дифракцияланған, вертикаль айналу өсіне параллель барлық дақтар горизонталді жазықтықта жатады. Басқа бағытта орналасқан жазықтықтар горизонталь жазықтықтан жоғары және төмен орналасқан шағылуларды береді.

Тәжірибе жүзінде осындай әдістің бірнеше түрлері қолданылады. Тербелу әдісінде кристалдың 360°-қа айналуының орнына оны шектеулі бұрыш интервалында тербелуге мәжбүр етеді. Бұл интервалдың шектеулігі түрлі ретті шағылысулардың болу ықтималдығын төмендетеді. Вейсенберг және прецессия әдісіндекристалдың тербелуімен қоса пленканың орын ауыстыруы орын алады.

Заманауи әдістерде дифрактометрлерді қолданады, онда дифракцияланған шоғырларды тіркеу үшін сцинтилляциялық немесе ионизациялық есептегіштерді (Гейгер-Мюллер есептегіші) пайдаланады. Оның арқасында эксперименттің автоматталынуы мүмкін болды, өйткені күрделі құрылымдар үлкен шамамен 10000–ға жуық шағылуларды бере алады. Қазіргі таңда мыңға жуық бейорганикалық және органикалық монокристаллдардың құрылымы анықталған.

Ұнтақтау әдісі (Дебай-Шерерр әдісі). Бұл әдісте монохроматты сәуле шоғыры 1 жұқа қабырғалы капиллярлы түтікшеге қойылған, майда ұнтақ немесе түйіршікті түріндегі, кристалиттері кездейсоқ орналасқан поликристалды материал үлгіге 2 түседі.

 

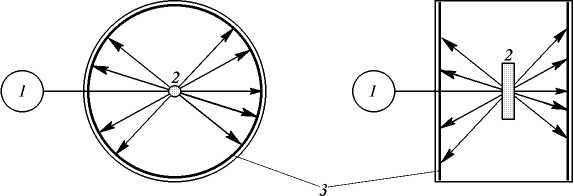
2.4-сурет - Ұнтақ (Дебай – Шеррер) әдісінің сұлбасы

 

Кристаллиттердің сызықтық өлшемдері 0,01мм-ден аспауы керек, әйтпесе эквивалентті емес кристаллографиялық жазықтардың орналасу бағыттарының жиынтығы жеткіліксіз болады.

Қандай да бір кристалит үшін дифракцияланған шоғыр (5.11) шартын қанағаттандырады, түзілген шоғырланған конустар бағытына қарай үлгіден шығады. Шоғырланған конустар өсі түсетін шоғыр бағытына бағыттас болады. Түсетін шоғырға перпендикуляр жазықтыққа орналастырған жазық фотопленкаға шоғырланған аймақ сериясы тіркеледі. Әдетте, цилиндр түрінде фотопленка 3 орналасқан цилиндрлік камералар қолданылады. Осы әдіс сцинтилляциялық немесе ионизациялық счетчигі бар дифрактометр негізінде жүзеге асуы мүмкін. Дебаеграмма сызықтарының интенсивтілігі мен орналасуы берілген заттың сол немесе басқа да кристалдық фазалары үшін жеке-жеке болады. Кристалдық құрылымның кез-келген өзгерісі, мысалы, фазалық ауысым нәтижесінде, дебаеграммасын ауыстырады. Ақаулардың бар болуы сызықтарды кеңейтеді. Дебай-Шеррер әдісін кристаллдық фазада екі немесе одан да көп түрлі заттары бола алатын қатты денелердің фазалық құрамын талдау үшін жиі қолданады.

 

2.3. Лауэ теңдеуі. Эвальдо түзілімі

Дифракциялық сурет пен кері тор қалай байланысты болатынын қарастырайық. Рентгендік сәуленің серпімді шашырауы кезінде квант энергиясы өзгермейді:

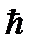ω = 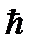ω^/, ω = сk, ω^/ = ck^/ (2.12)

мұнда с - электромагнитті толқын жылдамдығы, толқын векторының 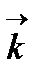ұзындығы өзгермейді, және нәтижесінде шашыраған толқынның толқындық векторы үшін мына теңдеу орындалады:

|k'| = |k| = 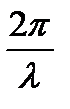(2.13)

 

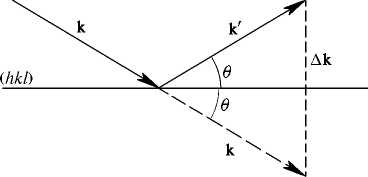
2.5-сурет - Шағылысқан толқынның толқындық векторының өзгерісі

Дифракциялық шашырау суретінде векторлық үшбұрыштан (2.5-сурет.) ∆ векторы (hkl) жазықтығына перпендикуляр болатындығы көрсетілген, яғни бағыты жазықтыққа 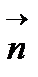нормаль түсірілген бірлік векторының бағыты секілді және кері тор векторы болып табылады да мына түрде жаза аламыз:

 

∆ = - ^/ = 2dsin 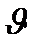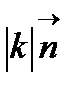= (5.14)

(2.14) теңдеуде (hkl) жазықтығына перпендикуляр кері тор векторларының белгіленулері қабылданған:

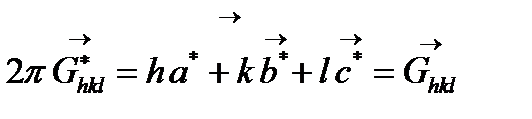(2.15)

Егер 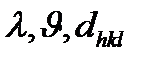мәндері Вульф – Брэгг заңы орындалатындай болса, онда (5.14) мына түрде жазуға болады:

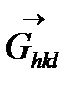∆ = (2.16)

Осылайша, 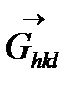векторымен құрылған көп нүктелер Лауэнің дифракциялық тәжірибесінде көрсетілген дақтардың үлестірілуіне сәйкес келеді. Осы нүктелер арасындағы қашықтық тура тордағы жазықтықтар арасындағы арақашықтыққа кері пропорционал.

Дифракцияны бастан кешірген толқынның бастапқы және соңғы толқындық векторы үшін теңдеу:

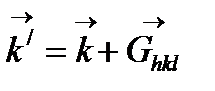(2.18)

Екі жағын шаршыға келтіріп мынаны аламыз:

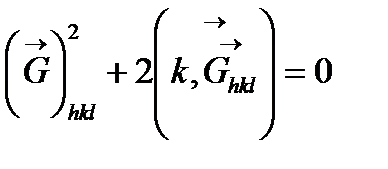(2.19)

(2.19) теңдеуі – тағы бір Вульф-Брэгг заңының жазбаша түрі.

Кері кеңістікте дифракциялық суреттің көрінісін Эвальдо түзілімі береді.

Эвальдо түзілімі.

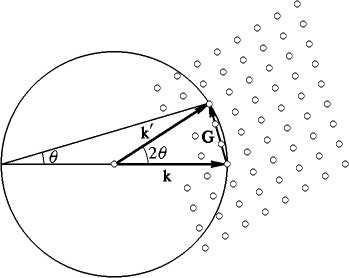
2.6-сурет. Эвальдо түзілімі

 

2.6-суреттің оң жағындағы нүктелер – ол кристалдың кері торының түйіндері. векторының бағыты кристалға түсетін рентгендік сәуле (нейтрондар шоғы). бағытымен сәйкес келеді. векторы кері тордың еркін түйінінде аяқталады. Суретте радиусы |k| = 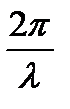, центрі векторының басы болатын сфера көрсетілген. Егер осы сфера кері тордың қандай да бір басқа түйінімен қиылысса және ∆ = 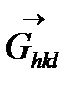болса, онда дифракцияланған сәуле түзіледі. Дифракцияланған сәуле векторы бағытына қарай кеңейеді.

Эвальдо түзілімі нейтрондардың дифракциясын рентгенді құрылымды талдауда кең қолданылады.

Лауэ дифракциясының теңдеуі.

Тура және кері тордың трансляция туындысы теңдеуінен мынаны аламыз:

 

(2.20)

Өзара ∆ векторы мен hkl үштік индекстерін және тура тордың базисті векторларын байланыстыратын осы қатынас Лауэ дифракциясының теңдеуі деп аталады.

 

2.4. Шашыраған (дифракцияланған) толқын амплитудасы үшін Лауэ теңдеуі

Екі шашыратқыш О және О'центрлер болсын делік (2.7-сурет), және шашыратқыш нүктелердің орны бүтін санды компоненттері бар векторлармен:

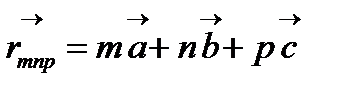(2.21)

Мұнда m,n,p – 0 ден М ге дейінгі шегіндегі бүтін сандар. Осы жағдайда кристаллда М³ ұяшық болады.

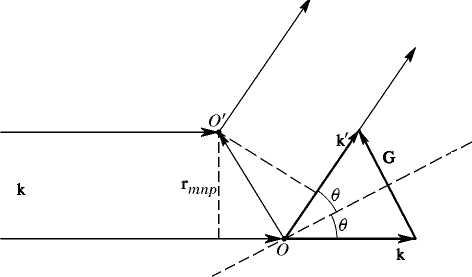
2.7-сурет - Екі центрдегі шашырау

 

Шашыратқыш центрлердің бірін координаталар басы деп таңдап алайық. Оған түскен бастапқы жазық толқын осы центрлерді қоздырады және әрқайсысы қосымша сфералық толқынның көзі болып табылады. Бастапқы толқын екі центрге түрлі фазалармен келеді, сондықтан түрлі бастапқы фазалар шашыратқын толқында да болады.

О және О^/ центрлерінен шашыраған толқындардың арасындағы фазалар айырымын табамыз:

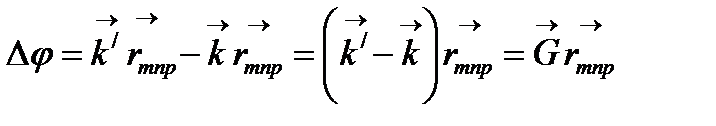(2.22)

Егер бастапқы толқынның бірлік амплитудасы (А = 1) болса, онда О^/ орнындағы шашыратқыш центрдің беретін толқыны:

(2.23)

Коэффициент f центрдің шашыратқыш икемділігі деп аталады. 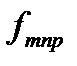шашыратқыш икемділігі бар барлық нүктелер 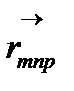үшін соңғы қорытынды толқынның амплитудасы:

(2.24)

F шамасы шашыратқыш амплитудасы деп аталады. (2.24) теңдеуінің сипаты алуан түрлі. Рентгенді сәуле үшін оларды шашырататын физикалық нүкте болып электрондар табылады. Егер бір электронның шашыратқыш икемділігінің мәнін бірге тең деп алсақ, онда оған қатысты шашыратқыш амплитудасы қарапайым түрге енеді:

(2.25)

Егер ∆ Лауэ дифракциясы теңдеулерін қанағаттандыратын болса, онда оларды (2.25) теңдеуіне қойып мынаны аламыз:

(2.26)

Мұнда (mh+nk+pl) қосындысы бүтін санды мәнді қабылдайды. Шашыраудың ең қарапайым жағдайы кристаллда тығыздығы орташа уақыт бойынша орналасқан электрондардағы шашырау болып табылады. нүктесінің маңында ∆V көлемде орналасқан электрондардың орташа саны арқылы орташа электронды тығыздықты анықтайық:

 

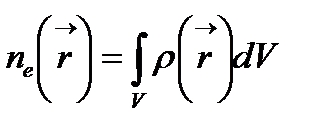(2.27)

Бірқалыпты функциядағы немесе электронды тығыздықтағы шашырауды қарастыра отырып, F шашырауының амплитудасын табу үшін дискретті нүктелер бойынша сомасынан интегралдауға көшу қажет:

(2.28)

Мұнда x, y, z тура кеңістіктегі нүктенің координатасы, кері кеңістіктегі шашыратқыш векторының координаттары.

Электронды тығыздықтың үлестірілуі элементар ұяшықта орналасқан өзара байланысты атомдардың электрондарының 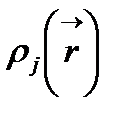үлестірілуімен анықталады. Әрбір ұяшықтың s атомы бар делік. j-ші атом центрінің орналасуы мына векторлармен анықталады:

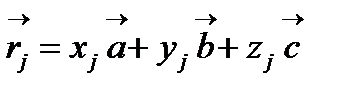(2.29)

Вектор түйінінен жүргізілген: 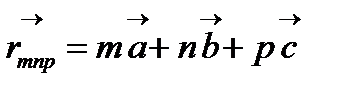. Бұл түйін қарастырып отырған ұяшықпен тығыз байланысты және оны mnp деп белгілейміз. Координаталар басын 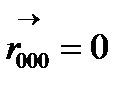деп таңдап аламыз. Осы координаталар басына қатысты j-ші атомның орналасуы вектормен анықталады. Атомдағы электрондар ядроға жақын жинақталмайтындығы белгілі, олар оның жан жағында орналасады. Мына функция mnp ұяшығында j – ші атомның маңындағы 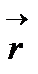нүктесіндегі электрондардың

(2.30)

концентрациясын анықтайды. Кристаллдағы электронды тығыздықтың үлестірілуін жеке атомдардың электронды тығыздықтарының суперпозициясы (5.30) ретінде қарастыруға болады. Кристаллдың толық электронды тығыздығын мына қосынды түрінде жазуға болады:

(2.31)

Мұнда бірінші қосынды базистердің барлық атомдары (j = 1,2,3,…s) бойынша жүзеге асады, ал екіншісі саны М³ –ге тең болатын, тордың барлық түйіндері арқылы жүзеге асады. ∆ шашыраудың жалпы амплитудасын мына түрде жазуға:

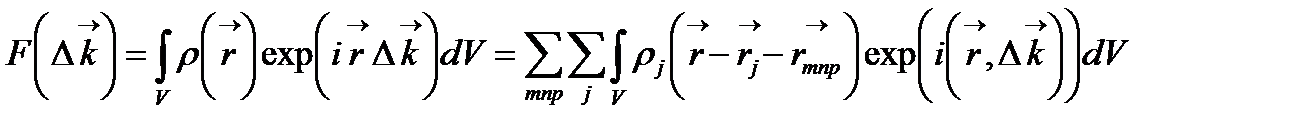(2.32)

Түрлендіреміз және мына шаманы енгіземіз:

(2.33)

шашыраудыңатомдық факторы, яғни j – ші атомдағы шашырау өлшемі. Сонда:

(2.34)

 

Бірінші қосынды М³-ке тең. ∆ шашырау векторы Лауэ дифракциясы теңдеуін қанағаттандырғандықтан, (2.34) теңдеудің маңыздысы болып дөңгелек жақшадағы екінші мүшесі – құрылымдық факторсаналады:

(2.35)

Параллель жазықтарды (hkl) жинақтау үшін құрылымдық фактор мына түрде болады:

(2.36)

Құрылымдық фактор комплексті сан бола алады. Нөлдік мәндер маңызды. h,k,l индекстерінің нақты бір мәндері үшін рефлекстердің болмауы өшу заңыдеп аталады.

 

3.Бөлім. Кристалдардағы ақаулар

 

Атомдары қатаң тәртіппен периодты түрде орналасқан кристалдар идеал кристаллдар деп аталады. Барлық нақты кристаллдардың құрамында идеал құрылымнан ауытқулар кездеседі, мұндай ауытқуларды құрылымның ақаулары деп атайды. Құрылымның ақауларын динамикалық және статистикалық деп бөлуге болады. Динамикалық ақауларға жылулық тербелістерден немесе электромагнитті өрістің кристалл арқылы өткенде атомдардың тербелістерінен туындайтын, кристалдық тордың бұрмалануын жатқызуға болады. Бұл ақаулар жақсы қарастырылған, олар атомдардың тепе-теңдік қалпына қатысты ығысуымен байланысты, олар идеал кристаллдарда да кездеседі. Осы бөлімде қарастырылатын статикалық ақаулар, кристалды тордағы атомдардың орындарының бұзылуымен байланысты, мысалы, тор түйініндегі бір атом жоқ немесе басқа түйінге орналасады немесе атомдар жинақталып кристалл ішінде үлкен ақау түзеді.

Статистикалық ақауларды пішініне қарай төрт топқа бөлу қалыптасқан: 1) нүктелік ақаулар, сызықтық ақаулар - дислокациялар; 3) беттік ақаулар; 4) көлемдік ақаулар.

Кристалдардың көптеген физикалық қасиетері ақауларға қатты байланысты. Мысалы материалдың мықтылығы мен созылмалылығы оның сызықтық, беттік және көлемдік ақауларына байланысты. Электр кедергісі негізінен нүктелік ақауға байланысты. Кристалдардың боялуы, диффузия коэффициенті, жылуөтімділігі де ақаулардың болуына қатты байланысты.

3.1. Нүктелік ақаулар

Нүктелік ақаулар – ең кіші ақаулар, әдетте бір атомның болмауымен, немесе бір атомның артық болуымен байланысты. Түрлі нүктелік ақауларды қарастырайық, олардың сызбасы 28-суретте көрсетілген.

Вакансия. Кристалдық тордың қандай да бір түйінінде атом болмауы мүмкін (3.1-сур.(1) қара). Мұндай бос орын вакансия деп аталады. Вакансияны жиі - Шотки ақауы деп те атайды.

Түйінаралық атом. Атом кристаллды тордың түйінінде емес түйіндер арасында орналасуы мүмкін (3.1-сур. (2) қара), мұндай ақау түйінаралық ақау деп аталады.

Френкель ақауы. Вакансия мен түйінаралық атомдар жиі жұп болып кездеседі (3.1-сур. (3) қара), бұл жағдайда атомдардың бірі түйіндегі орнынан көрші түйінаралық орынға секіріп өтіп кетеді. Мұндай секірістің себебі салыстырмалы түрде жоғары температурада, мысалы, балқу температурасындағы жылулық қозғалысы немесе жылдам бөлшек пен атомның соқтығысуы кезінде өз орнынан ығыстыруы (радиациялық ақау) бола алады. Ақаулардың мұндай жұптары Френкель бойынша ақаулар деп аталады.

Қоспа атомы. Атомдардың бірі қоспа атомы болуы мүмкін (3.1-сур. (4) қара), мұндай жағдайда да ақау түзіледі және ол орнын басатын қоспа атомы деп аталынады. Қоспалы атом қалай да еніп түйінарасына орналаса алады (3.1-сур. (5) қара), мұндай ақау енгізілген қоспа атомы деп аталады.

3.1-сурет - Нүктелік ақаулардың түрлері: 1 - вакансия; 2 – түйінаралық атом; 3 - Френкель бойынша ақау; 4 – қоспалы орнын басу атомы; 5 – енгізілген қоспалы атом; 6 – жоғары валентті орнын басу атомы

Кристалл атомдарынан валенттілігімен ерекшеленетін қоспа атомдары вакансиялардың пайда болуын негіздейді, мысалы KCl кристаллы жалпы жағдайда нейтральді болатындай етіп оған Ca қоссақ. Бұл жағдайда екі валентті кальцидің атомы калийдің бір атомының орнын алады, ал калий атомы болу керек орын бос болады (3.1-сур. (6) қара).

Нүктелік ақаудың энергиясы және оның пайда болу ықтималдығы.

Нүктелік ақау мен ақаулардың түзілу энергиясы E_V тығыз байланысты. Вакансия кезінде бұл энергия атомды кристаллдың бетіне шығарып тастау үшін қажет, ал енгізген атом кезінде бұл энергия атомның кристалл бетінен түйінаралық орынға жылжуы үшін қажет. Тәртіп бойынша, оның мәні шамамен 1 эВ құрады. Нүктелік ақаудың түзілуінің ықтималдығы Больцман теңдеуі арқылы шығарылады:

(3.1)

Осы теңдеумен шығарылатын P ықтималдығы E_V=1эВ және Т=1000⁰К, болғанда мынаған тең

Френкель бойынша ақау кезінде, ақаулар жұбын түзу үшін (вакансия мен түйінаралық атом), саны жағынан атомды кристалл бетіне шығарып тастауға, сосын атомды кристалл бетінен түйінаралық орынға жылжытуға қажет энергияға тең энергия E_Fr керек. Осындай ақаулар санының мына теңдеу арқылы есептелетіндігін көрсетуге болады:

(3.2)

мұнда ;N_A және N_M сәйкесінше кристалдағы түйіндер мен түйінаралықтардың саны.

 

3.2. Сызықтық ақаулар

Дислокация деп аталатын кристалды тордың сызықтық ақауларын тереңірек зерттеу, олардың барлық кристалды материалдардың беріктігі мен икемділігіне қатты әсер етуімен байланысты. Осы ақаулардың болуын ескермеген кристаллдардың беріктік теориясы монокристаллды және поликристаллды заттарда байқалған механикалық қасиеттерді түсіндіре алмады.

Дислокацияның типтері. Дислокацияны аймақтық және бұрандалы деп екіге бөлу қалыптасқан, дегенмен байқалатын дислокацияларда әдетте осы екі типтің элементтері бола береді. Қарапайымдылық үшін жәй кубты торды қарастырайық, бірақ алынған нәтижелер шамалы өзгерістермен басқа да типтердің торлары үшін дұрыс.

Аймақтық дислокация атомдардың ерекше орналасуымен сипатталады, 3.2-суретте қарапайым кубты тор көрсетілген. Бұл суретте 100 типіндегі екі көрші бүтін жазықтар арасына орналастырған жазықтықтың "артық жартысы" бейнеленген. Бүтін жазықтардың атомдары бір-бірімен байланыстарын қалыптастырды, бірақ енгізілген жарты жазықтықтың шетінде үлкен деформация пайда болды. Артық жарты жазықтықтың шеті арқылы өтетін сызықты аймақтық дислокация сызығы деп атайды, кейде жәй аймақтық дислокация деп те атайды. Сондықтан да дислокацияны сызықтық ақауларға жатқызады. Ол артық жарты жазықтықтың шеті орналасқан, осы жарты жазықтық әсерінен болатын кристалдық тордың күшті майысқан жері арқылы өтеді. Кристалдық тордың дислокациясы маңындағы күшті майысқан облысы 2-3 периодқа созылады. Үлкен арақашықтықта бұрмалану аз болады және оларды серпімділік теориясында қарастыруға болады.

3.2-сурет - Дислокация жанындағы атомдардың орналасуының сұлбасы

 

Аймақтық дислокация 3.2-суретте көрсетілгендей сызба бойынша кристалдардың деформациясы кезінде жиі кездеседі. Сырғу жазықтықтары деп аталатын, атомдары тығыз орналасқан жазықтықта жылжу деформациясы болған кезде дислокация пайда болады.

{100} типіндегі жазықтығы бар қарапайым кубты тор жағдайын қарастырамыз. КЦК торы үшін сырғу жазықтықтары - {110}, {112}, және {123}, ал ҚЦК торлары үшін - {111} болып табылатынын айтып кетейік. Егер кристаллға күш әсер етсе (3.3-сур.(1) қара), онда (100) жазықтығы пунктирмен белгіленген жерге дейін "жыртылуы" мүмкін (3.3-сур. (2)), одан кейін 1 жазықтығының жоғарғы жартысы төменгі жартыға қосылады 2 (3.3-сурет (3)), ал 2 жазықтығының жоғарғы жартысы "артық" болып қалады. Егер кристалға әсер етуді жалғастырсақ, онда келесі жазықтық бөлініп кетеді де, кейін 2 жазықтығының жоғарғы жартысы 3 жазықтығының төменгі жартысына қосылады (3.3-сурет (4)), және т.с.с. жалғаса береді. Осылайша кристаллда артық жарты жазықтық (100) пайда болады, ол күшінің әсерінен көрші жарты жазықтықтардың қосылу-айырылуы арқасында сырғу жазықтығы бойынша жылжи береді. Жаңа жазықтықтың айырылуы дислокация сызығының бойында жүзеге асады, өйткені онда кристалдық бұрмалану жоғары болады (3.3-сурет.).

 

3.3-сурет - Кристалдың жылжымалы деформациясы кезіндегі аймақтық дислокацияның туындауы мен орын ауыстыру сұлбасы

 

Бұрандалы дислокация. Бұрандалы дислокация3.4-суретте қарапайым куб үшін көрсетілген, атомдардың ерекше орналасуымен сипатталады. Осы суретте А жарты жазықтығының сол жағында орналасқан атомдар орындарында қалған, ал оның оң жағындағы атомдар бір жазықтық арасы қашықтығына төмен ығысқан. Мұндағы В сызығының жанында үлкен деформация пайда болған. А жарты жазықтығының қыры арқылы өтетін В сызығын және қалған жарты жазықтықты бұрандалы дислокация деп атайды. 3.4-суретте (001) типіндегі горизонталь деформацияланған жазықтықта В сызығы бойынша айналу кезінде кристалдық тордың бір периодына көтерілуге болады, ал В сызығы бойынша бірнеше рет айналған кезде тордың бірнеше периодына көтерілуге болатындығы көрсетілген.

Көтерілу бұрандалы автожол бойынша қозғалысқа ұқсас, осыдан бұрандалы дислокация ұғымы пайда болды. Бұрандалы дислокация жағдайында барлық (010) жазықтықтар өзімен өзі бола алмайды, олар өсі В болатын күрделі бір бұрандалы бетке бірігіп кетеді. 3.4-суретте көрсетілген бет В сызығын айнала сағат тілшесіне қарсы қозғалысы кезінде көтерілісті қамтамасыз етеді (егер жоғарыдан қараса). Мүмкін В сызығын айнала сағат тілшесімен қозғалған кездегі көтерілісті қамтамасыз ететін дәл сондай бет түзген шығар (ол үшін 3.4-суреттегі кристаллдың оң жағын төменге емес жоғары қарай ығыстыру керек еді). Сондықтан бұрандалы дислокация оң бұрандалы және сол бұрандалы болады.

3.4-сурет - Бұрандалы дислокацияға атомдық жазықтардың жақын орналасу сұлбасы

3.4-суретте көрсетілген сызба бойынша бұрандалы дислокация кристалдың деформациясы кезінде пайда болады. {100} типіндегі жазықтықты қарапайым кубты тор жағдайында қарастырамыз. Егер кристалға күшімен әсер етсек (3.5-сурет (а)), онда бағытталған кесіндімен белгіленген орында А1 жазықтығы В сызығы бойынша "айырылады", одан кейін А1 жазықтығының жоғарғы және төменгі жартылары тордың 1 периодына жылжумен қосылады (3.5-сурет (б)). Егер кристалға әсер етуді жалғастырсақ, онда келесі жазықтық айырылады А2 жазықтығының үстіңгі және жоғарғы жартылары жылжумен қосылады (3.5-сурет (в)), және т.с.с. жалғаса береді. Осылайша, кристалда бұрандалы дислокация пайда болады, ол кристалға әсер еткенде жазықтықтардың көрші жартыларының қосылу-айырылуы арқасында сырғу жазықтығы бойынша жылжи береді. Жаңа жазықтықтың айырылуы дислокация сызығының бойында болатынын ескеру керек, өйкені онда кристалдық тордың бұрмалануы көбірек болады (3.5-суретке қара).

а) б) в) 3.5-сурет - Кристалдың жылжымалы деформациясы кезінде бұрандалы дислокацияның туындауы мен орын ауыстыруының сұлбасы

Бюргерс векторы. Бұрандалы дислокацияны кристаллдың келесі модельді операциялар арқылы алуға болады (3.6-суреттегі (а)). Кристаллда (100) жазықтығы бойынша, кристаллды тор түйіндері арасынан өтетін, А жарты жазықтығынан ойша қиық жасайық. Сосын оның оң жағындағы атомдарды төмен қарай бір жазықтық аралық қашықтыққа жылжытып,атомдарды қайтадан А арқылы өтетін байланыспен байланыстырайық. Кристалдың оң жағындағы векторға қатысты сол жағындағы ығысу векторы В бұрандалы дислокациясының Бюргерс векторы деп аталады.Бұрандалы дислокациясының Бюргерс векторы осы дислокацияға параллель болатындығы көрініп тұр.

3.6-сурет - Аймақтық және бұрандалы дислокация кезіндегі кристалдағы атомдардың ығысу сұлбасы. - Бюргерс векторы

Дәл осындай әдіс арқылы аймақтық дислокацияны да алуға болады (басқа сырғу жазықтығына жауап беретін). Ол үшін кристалдың «оң» жағын А жазықтығы бойынша «бізден ары қарай» ығыстыру керек және В дислокациясы сызығының бойында орналасқан атомдардан басқа барлық атомдар арасындағы байланыстарды жетілдіру керек (3.3-суреттегі (а)). Кристалдың осы бөлігіндегі ығысу векторы аймақтық дислокацияның Бюргерс векторы болады. Аймақтық дислокацияның Бюргерс векторы дислокацияға перпендикуляр болатындығы көрініп тұр.

Дислокация тығыздығы. Дислокацияны бақылау әдісі. Кристалдарда дислокация тығыздығы кристалл ішінде таңдалған, бірлік бетті қиып өтетін дислокация санымен сипатталады, немесе, басқаша айтқанда, кристаллдың бірлік көлеміндегі дислокация ұзындығының сомасымен сипатталады. Дислокация тығыздығының мәні және осы дислокация тығыздығына қолданылатын олардың бақылау әдістері төмендегі 7-кестеде көрсетілген

 

7-кесте.Дислокация тығыздығының мәні және оларды бақылау әдістері

 

Дислокацияны зерттеу әдістері	Үлгінің қалыңдығы, мкм	Дислокация бейнесінің ені, мкм	Дислокацияның 1см2 дегі максималді тығыздығы
Электрондық микроскопия	10-0-10-1	10-2	1011-1012
Рентгендік топография (өтімділік үшін)	102-103		104-105
Рентгендік топография (шағылысу үшін)	2-50		106-107
Оптикалық микроскопия (өңдеу шұңқырлары бойынша)	Кез-келген	0,3-0,5	10-6-10-7

Кез-келген тығыздықтағы дислокацияны электронды микроскоп арқылы, ал жақсы жетілдірілген, идеал монокристалдардағы дислокацияларды рентгендік топография (идеал, жетілдірілген кристалл арқылы өткен рентгендік сәуленің интенсивтілігін өлшеуге немесе суретке түсіруге негізделген әдіс) арқылы байқауға болады. Дислокацияны бақылау әдістері дислокацияның өзін емес, кристалдық тордың бұрмалануын көрсететіндігін айту керек.

Кейде дислокацияның іздерін арнайы таңдалып алынған химиялық өңдеу арқылы кристалдың бетіндегі «өңдеу шұңқырлары» бойынша байқауға болады. Бұл әдіс мынаған негізделген, өңдеуші кристалдық тордың дислокациясы маңындағы бұрмалау жақтарын қатты ерітеді, сондықтан дислокацияның кристалл бетіне шығатын орындарында шұңқырлар көрінеді. Жарық микроскобын пайдалану барысында оның рұқсат ету шегі 0,5-1 мкм–ге дейін болатындығын ескеру керек, яғни дәл осындай арақашықтықта орналасқан "өңдеу шұңқырлары" бөлек-бөлек болып көрінеді, ал дислокацияның тығыздығы жоғары болғанда бірігіп кетеді.

 

3.3. Беттік және көлемдік ақаулар