Монокристалдар. Поликристалдар

Қатты денелер (кристалдар) молекулааралық әсерлесу күштерiнің болуымен сипатталады және көлемiн ғана емес, сонымен қатар пішінін сақтайды.

Кристалдар геометриялық пішіні дұрыс, немiс физигі М. Лауэнің рентгенографиялық зерттеу жұмыстары көрсеткендей, ол кристалды құрайтын бөлшектердiң (атомдар, молекулалар, иондар) ретпен орналасуының нәтижесі болып табылады. Үш өлшемді кеңістікте үнемі (периодты түрде) қайталанумен сипатталатын бөлшектердің орналасуы кеңістіктік тор деп аталады. Бөлшектер орналасқан нүктелер кристалдық тордың түйiндерi деп аталады.

Кристалды денелерді екі топқа бөліп қарастыруға болады: монокристалдар және поликристалдар. Монокристалдар– бөлшектері біртұтас кристалдық тор құратын қатты денелер. Монокристалдардың кристалдық құрылымын сыртқы пішініне қарап айтуға болады. Бір типтегі монокристалдардың сыртқы пішіні әр түрлі болғанына қарамастан онда тиiстi қырлардың арасындағы бұрыштар тұрақты болады.

Бұл 1669 жылы Николай Стенон ашқан бұрыштың тұрақтылық заңы және кристаллографияның осы бiрiншi сандық заңы былай тұжырымдалады: бір типтегі заттың барлық кристалдарында бiрдей жағдайда (температура және қысым бiрдей болғанда) сәйкес кристалл қырларының арасындағы бұрыштар тұрақты болады.

Бұрыштардың тұрақтылық заңы кристалдық көпқырлылардың сан қилы пішіндерін қырлар арасындағы бұрыштар жиынтығына келтіруге және оларды проекция көмегімен бейнелеуге мүмкіндік береді. Рентгендік сәулесі дифракциясын және рентгеноқұрылымды талдау ашылғанға дейін кристалдарды бір бірінен тек қырлары арасындағы бұрыштар арқылы ғана сипаттап және бір-бірінен ажырата білген.

Монокристалдарға көптеген табиғи минералдар: мұзды, ас тұзын, исланд шпатын жатқызуға болады. Қазіргі таңда көптеген монокристалдар жасанды түрде өсіріледі. Ірі монокристалдарды өсіру шарты жиі ұстала бермейді, сондықтан қатты денелердің көпшілігінің кристалдық торлары ұсақ кристалды құрылым түрінде болып келеді, яғни көптеген ретсіз орналасқан ұсақ кристалдық түйірлерден тұрады. Мұндай қатты денелер поликристалдар(көптеген тау жыныстары, техникалық металлдар мен ерітінділер) деп аталады.

Монокристалдарды сипаттайтын ерекшелік олардыңанизатроптығы,яғни физикалық қасиеттерінің (серпімділік, механикалық, жылулық, электрлік, магниттік, оптикалық) бағытқа тәуелділігі.Монокристалдардың анизотропиясын мына түрде түсіндіруге болады: кристалдық торда ұзындықтары бойынша бірдей, ал бағыты бойынша түрлі болатын кесіндіге келетін бөлшектердің саны әртүрлі, яғни кристалдық тордағы бөлшектердің орналасу тығыздығы түрлі бағытта бірдей болмайды, сәйкесінше осы бағыт бойынша кристалл қасиеттері де түрленеді. Поликристалдарда анизотропия тек жеке ұсақ кристалшалар үшін байқалады, бірақ олардың әр түрлі орналасуына байланысты барлық бағыт бойынша поликристалдың қасиеті орташа алғанда бірдей.

1.2. Кристалдың трансляциялық симметриясы. Негізгі векторлар

Қатты дене физикасының тарихындағы маңызды кезең Макс фон Лауэ рентген сәулесінің дифракциясы арқылы кристалл атомдардың периодты қатарынан тұратындығын дәлелдеген 1912 жыл болып саналады.

Атомдардың ретпен орналасуы қатты дененің термодинамикалық тепе-теңдік күйіне сәйкес келеді, яғни кристалл – бұл жеткілікті төмен температурада атомдар жүйесінің тепе-теңдік күйі. Барлық қатты денелер кристалдық бола бермейді: мысалы, балқыған немесе еріген затты тез суытқан кезде ''мұздатылған сұйықтықты'' – атомдары ретсіз орналасқан, аморфты қатты денені алуға болады. Мұндай қатты денелердің мысалы ретінде қарапайым шыныны алуға болады. Кристалда атомдардың ретпен орналасуы деп оның кеңістіктіктегі периодтылығы мегзеледі. Басқаша айтқанда, әрбір кристалл үшін бір жазықта жатпайтын және кристаллды біртұтас түрінде осы векторлардың кез келгеніне орын ауыстырғанда өзіне-өзі қайта беттесетін 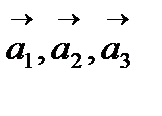үш вектор таңдап алуға болады.

Кристалдың векторына орын ауыстыру операциясы трансляциядеп аталады, мұндағы n1, n2, n3 — бүтін сандар. Кристалдар трансляциялықсимметрияға ие дейді, өйткені векторына трансляциялану барысында ол өзіне өзі беттеседі. 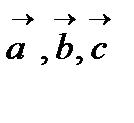векторларын түрлі әдістермен таңдап алуға болатындығы анық (1-суретті қара). Осы векторлар арқылы жасалған параллелепипед элементар ұяшықдеп аталады. Минималь көлемді ұяшық примитивті ұяшық, ал ол құрылған 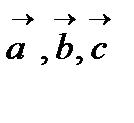векторлары трансляцияның примитивті немесе негізгі векторлары деп аталады. Кейін де трансляцияның басты векторлары дәл осылай белгіленеді. векторларын біз тура тордың векторлары деп атаймыз. Осылайша, примитивті ұяшық элементар ұяшықтың жеке жағдайы болып табылады. Басты векторларды да түрлі әдістермен таңдауға болады.

1-суретте екі негізгі және негізгі векторлардың екі мүмкін жұптары келтірілген, ал екі мүмкін болатын негізгі векторлардың жұбы, ал ,— трансляцияның негізгі емес векторлары.

Примитивті ұяшықтың көмегімен трансляцияның кейінгі операциялары арқылы, кристалдық құрылымның барлық кеңістігін толтыруға болады. Примитивті ұяшық – бұл кеңістікте периодты түрде қайталанатын, параллелепипед пішінді, әр нүктесінде атомдар жиынтығымен байланысты кристалдық тордың бір бөлігі. Мұндай атомдар жиынтығын базис деп атайды, базис кеңістікте қайталанадыжәне кристалдық құрылымды түзеді.

Трансляцияның негізгі векторымен құрылған кристалдың примитивті ұяшығы бар делік. Кеңістіктегі бір нүктені алып және 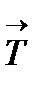векторына осы нүктенің трансляциясы арқылы нүктелерден тұратын кеңістіктік торды аламыз, мұндағы n1, n2, n3 барлық бүтін сандарды алады. Осы тордағы барлық нүктелер (түйіндер) эквивалентті, яғни айналасы бірдей болатындығын көре аламыз (басқаша айтқанда, әрбір түйіннен қарағанда тордың бір бейнесін ғана көре аламыз). Осындай торлар Бравэ торларыдеп аталады. Бравэ торлары кристалдың трансляциялық симметриясын толықтай көрсетеді. Трансляцияның негізгі векторлары келесі шарттарды қанағаттандыруы керек: Бравэ торының қандай да бір түйінінен басталатын және оның бойында құрылған тура тордың векторлары Бравэ торының барлық басқа түйіндерінде аяқталуы қажет, яғни тура тордың векторларының ішінде берілген Бравэ торының кез-келген екі түйінін қосатын векторлар табылады. Егер кристалдық тордың базисі бір ғана атомнан тұратын болса және бір примитивті ұяшықта бір ғана атом орналасса, онда кристалдық тор қарапайым деп аталады. Бұл жағдайда кристалдың барлық атомдары бір Бравэ торының түйіндеріне орналасады. Егер примитивті ұяшықты, оған тек бір атом сәйкес келетіндей етіп таңдап алу мүмкін болмаса, яғни базис бірнеше атомдардан тұрса, онда тор күрделі болады. Бұл жағдайда базистің әр атомына, өзінің бір типтегі атомдардан тұратын торшасы сәйкес келеді және ол кристалдың Бравэ торына ұқсас. Екіөлшемді күрделі тордың мысалы 1.1-суретте бейнеленген. Қара және ақ атомдар химиялық тұрғыдан ұқсас болуы мүмкін, бірақ ереже бойынша олардың кристалдық торларда орналасуы әртүрлі. Егер кристалдағы атомдар химиялық тұрғыдан ұқсас болса және олардың әрбірінің қай жағынан қарасаң да кристалдық тордың бір бейнесі көрінсе, онда сол атомдар бір типті болады. Осылайша, егер тек бір типті атомдарға ғана қарасақ Бравэ торын көре аламыз. Кристалды екі әдіс арқылы көзге елестетіп, түсінуге болады: базисті алып, трансляцияның примитивті векторлары көмегімен оны көп рет трансляциялау керек немесе бірнеше бірдей Бравэ торларын алып, оларды бірінің үстіне бірін орналастыру керек. Екіөлшемді кристалл, 1.1-суретте көрсетілгендей, бірінің үстіне бірін орналастырған екі Бравэ торынан тұрады

 

1.1 сурет. Екі өлшемді Бравэ торы

 

 

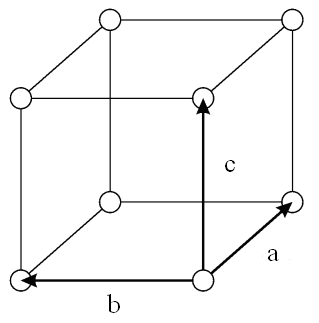
1.2 сурет.Қарапайым кубты тор

 

1.2–суретте қарапайым кубты тор көрсетілген. Қырғацентрленген кубты тордың әрбір ұяшығында бір ғана атом орналасқан (1.3–сурет).

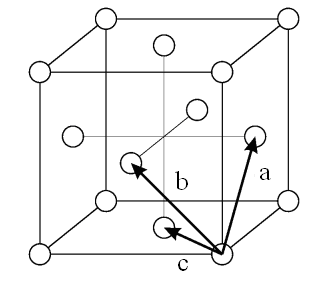
1.3 сурет.Кубты гранецентрленген

 

Егер кубтың ортасында атом болса, онда ол көлемді-центрленген кубты тор делінеді (1.4–сурет.).

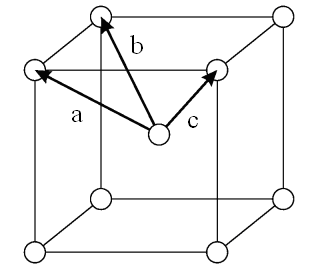
1.4 сурет.Көлемді-центрленген кубты тор

Сонымен, Бравэ торы кристалдың кұрылысын емес, оның трансляциялық құрылымын (симметриясын) көрсетеді. Трансляциядан басқа, кристалдардың нүктелік симметриясы: бұрылыс пен шағылысуға қатысты симметриясы болады. Нүктелік симметрияны анықтау үшін Бравэ торының типімен бірге, байланыс құрылыстарын да ескеру қажет (примитивті ұяшықтың базисі). Кейде қарапайым ұяшық дегенде базис пен примитивті ұяшықты көзге елестетуге болатындығын айтып кетейік. Бірнеше примитивті ұяшықтары бар және кристалдың нүктелік симметриясын көрсететін Бравэ торының бір бөлігін шартты немесе кристаллографиялық қарапайым ұяшық дейді. 1.2-1.4-суреттерде дәл осындай ұяшықтар бейнеленген.

 

1.3. Нүктелік симметрияның элементтері және түрленуі

Симметрия өсі.Түрлену: өсті айнала белгілі бір бұрышқа бұрылу α=360°/n, сәйкес келетін симметрия өсі Ln арқылы белгіленеді, n - симметрия өсінің реті деп аталады. 1.5-суретте L2 екінші ретті симметрия өсіне L3 үшінші ретті симметрия өсіне ие фигуралар көрсетілген. Егер фигура 360°/n бұрылу бұрышына қатысты симметриялы болса, онда ол k 360°/n бұрышын жасап Lnk –түрленуі кезінде де өзіне-өзі қайта келетіні анық, мұнда 1<k<n – бүтін сандар. Кристалдық торлардың (трансляциялық симметриясы бар фигуралар) симметриялық өсі тек 2, 3, 4, 6-ретті болып келетіні дәлелденген.

1.5-сурет.Екінші және үшінші ретті симметрия өсі

 

2.Симметрия жазықтығы.Түрленуі: жазыққа қатысты шағылуы, бұл симметрия элементі σ арқылы белгіленеді. Егер фигураның симметрия жазықтығы да, симметрия өсі де бар болса және симметрия жазықтығы симметрия өсі арқылы өтетін болса, онда осы симметрия жазықтығы Pv арқылы белгіленеді. Ал егер симметрия жазықтығы симметрия өсіне перпендикуляр болса, онда бұл элементті Ph арқылы белгілейміз.

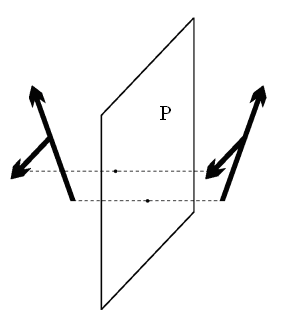
1.6-сурет.Симметрия жазықтығы

 

3.Қандай да бір нүктеге қатысты инверсия (симметрия центрі)- i әрпімен белгіленеді, сәйкес нүкте инверсия центрі деп аталады. Инверсия ортасы - ол симметрияның ортасы арқылы жүргізілген кез-келген түзу, фигура центрінің екі жағынан фигураның бірдей нүктелерені бірдей қашықтықтарда кездестіретін фигураның ішінде орналасқан ерекше нүкте.

Симметрия ортасындағы симметриялық түрлену - ол нүктедегі айналық шағылу.

4. Ретті инверсиялы-бұрылу өсi. Түрленуі: біртіндеп өсті айнала 360/n бұрышын жасап бұрылуы және жазықтықтың перпендикуляр өсiнде шағылу. n - тақ сандар болғанда, инверсиялы-бұрылу өсi симметрия өсіне Ln және оған перпендикуляр симметрия жазықтығына σh келтірілетіндігін көрсетуге болады.

4-ретті инверсиялы-бұрылу өсі бар фигура 1.7-суретте көрсетiлген.

 

1.7 -сурет.Төртінші ретті айналы-бұрылыс өсі

Lni түрленуін: Lni=Ph·Ln түрінде қарастыруға болады.

Осы теңдеудегі көбейту таңбасы іс-әрекеттің тізбектілігін білдіреді (оңнан солға): бастапқыда екінші көптік (Ln), сосын бірінші (Ph), яғни, бірінші бұрылыс орындалады, ал кейін шағылу жүзеге асады. Фигураның мүмкін болатын симметрия түрленуі неғұрлым көп болса, ол солғұрлым симметриялы болады. Кристалл симметриясы Бравэ торының симметриясынан жоғары бола алмайды(төмен бола алады). Бізде екі фигура болсын делік. Осы әр фигура үшін барлық симметрияның түрленуінің жиынтығын (тобын) табуға болады. Егер осы түрлену жиынтықтары бірдей болса, онда фигуралардың симметриялары да бірдей болады дейміз.

1.4.Бөлім. Топтар теориясы. Топтарды анықтау

 

{A,B,C,D...} элементтер жиыны болсын және бұл жиын келесі қасиеттерге ие делік:

1. Жиын элементтері үшін көбейтінді (композиция) ұғымы анықталған, яғни, кез-келген екі элементтер A және B үшін сәйкесінше осы жиынның үшінші элементі қойылады: A·B=C (толықтық қасиеті). Көбейтінді ретке байланысты, яғни коммутативті емес;

2. Кез-келген A үшін A·E=A қасиетіне ие жиын элементі Е бар (бірлік қасиеті). Басқаша айтқанда, осы жиында бірліктің (бірлік элементтер) болуын постулаттайды.

3. Кез-келген A элементі үшін осы жиында A–1 деп белгіленетін элемент бар және ол үшін: A·A–1=1 теңдігі орындалады. Бұл шарт кері элементтің бар болатындығын көрсетеді.

4. Көбейту ассоциативті: (A·B)·C=A·(B·C) болуы керек.

5. Бүтін сандар жиыны сандардың көбейту операциясына қатысты топтарды құра алмайды – кері элемент A–1 жоқ. Нақты сандар жиыны да арифметикалық көбейтуге қатысты топтарды құра алмайды, өйткені нөл үшін кері элемент жоқ. Нақты және бүтін сандар қосу операцияларына қатысты топтарды құра алады, мұндай жағдайда E=0, A–1=–A.

Теорема: Нақты бір фигураның барлық симметриясының түрлену жиыны, яғни фигура өзіне өзі қайта келетін жағдайдағы түрлену жиыны топтарды құрады. Осы топтың екі элементтерінің композициясы (көбейтіндісі) симметрияның түрленуінің тізбектей қолданысы болып табылады: A·B көбейтіндісі дегеніміз, бірінші болып B түрленуі орындалады, ал кейін A түрленуі орындалады дегенді білдіреді.

Дәлелденуі.Жиын фигураның барлық симметриясының түрленулерін қамтитындығынан толыққандық қасиеті шығады. Жеке элемент – түрленулердің (ұқсас түрленулер, E арқылы белгіленеді) болмауы; кері элемент — кері түрлену. Көбейтудің ассоциативтілігін дәлелдеуге болады.