Контроллеры, командоаппараты и реостаты

 

Задачи на определение времени решаются интегрированием уравнения движения (1) после разделения переменных. Для (что характерно для многих производственных установок, в которых и система управления обеспечивает постоянное среднее значение пусковых и тормозных моментов), а также при , в результате интегрирования уравнения (2), получим следующие расчетные формулы для вычисления времени пуска и торможения электропривода, с,

; (22)

. (23)

Так как путь, проходимый приводом при неустановившемся движении,

, (24)

то, используя уравнения (22) и (23), получим следующие выражения для определения пути электропривода за период пуска _п и торможения _т:

; (25)

. (26)

Для конкретных кинематических систем угловой путь двигателя пересчитывается в угловое или линейное перемещение ИМ.

Пример 4. Определить время пуска подъемника при опускании груза в двух случаях: а) двигатель развивает движущий момент = 160 Н·м; б) двигатель развивает тот же по величине тормозной момент.

Статический момент на валу двигателя активный и равен 320 Н·м. Момент инерции привода и подъемника, приведенный к валу двигателя, =15 Дж∙с². Установившаяся скорость двигателя об/мин ( 8,7 с^-1) .

Решение:

Пример 5. Тележка разгоняется электроприводом до номинальной скорости м/с при постоянном статическом моменте сопротивления. Момент инерции механизма, приведенный к валу двигателя, = 0,6 Н·м∙с², момент инерции двигателя = 0,15 Н·м∙с², номинальная скорость двигателя =1430 об/мин., динамический момент при разгоне тележки 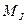= 100 Дж = . Определить время разгона тележки, путь тележки и двигателя за период разгона и их ускорения.

Решение. Время пуска тележки в соответствии с выражением (22)

Путь, пройденный тележкой за период разгона до скорости 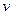= 1,5 м/с,

,

а ускорение при пуске тележки

Соответственно, угловой путь двигателя

Этот же результат получается, если вычислить

Угловое ускорение двигателя