Многогранники Архимеда
| Древне Греческому ученому Архимеду принадлежит открытие 13 многогранников - "архимедовых тел". Которые так же именуют полуправильными многогранниками. Каждое из них ограничено неодноименными правильными многогугольниками и в котором равны многогранные углы и одноименные многоугольники. Кроме того, в каждой вершине сходится одно и тоже число одинаковых граней. В одинаковом порядке каждое из этих тел может быть вписано в сферу. |
| 1. Усечённый тетраэдр | 
| 
|
| 2. Усечённый октаэдр | 
| 
|
| 3. Усечённый гексаэдр (другое название усечённый куб) | 
| 
|
| 4. Усечённый додекаэдр | 
| 
|
| 5. Усечённый икосаэдр | 
| 
|
| 6. Кубо-октаэдр | 
| 
|
| 7. Ромбо-кубо-октаэдр | 
| 
|
| 8. Ромбо-усечённый кубо-октаэдр | 
| 
|
| 9. Плосконосый куб (другое название курносый куб) | 
| 
|
| 10. Икосо-додекаэдр | 
| 
|
| 11. Усечённый икосо-додекаэдр | 
| 
|
| 12. Ромбо-усечённый икосо-додекаэдр | 
| 
|
| 13. Плосконосый додекаэдр (другое название курносый додекаэдр) | 
| 
|
Обратите внимание на тот, факт что в названии любого многогранника есть слово-основа. Именно эта основа позволяет определить к какому из пяти правильных многогранников относится текущий.
| Название | Слово-основа |
| Усечённый тетраэдр | тетраэдр |
| Усечённый октаэдр Кубо-октаэдр Ромбо-кубо-октаэдр Ромбо-усечённый кубо-октаэдр | октаэдр |
| Усечённый куб Плосконосый куб | куб |
| Усечённый додекаэдр Икосо-додекаэдр Усечённый икосо-додекаэдр Ромбо-усечённый икосо-додекаэдр Плосконосый додекаэдр | додекаэдр |
| Усечённый икосаэдр | икосаэдр |
Прародителем каждого из 13-ти полуправильных многогранников является один из пяти Платоновых многогранников.
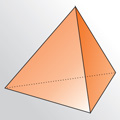
| => | 
| Из тетраэдра – усечённый тетраэдр |
Из октаэдра: усечённый октаэдр, кубо-октаэдр, ромбо-кубо-октаэдр, ромбо-усечённый кубо-октаэдр

| => | 
| 
| 
| 
|
Из куба: усечённый куб, курносый куб

| => | 
| 
|
Из додекаэдра: усеч. додекаэдр, икосо-додекаэдр, усеч. икосо-додекаэдр, Ромбо-усеч. икосо-додекаэдр, курносый додекаэдр
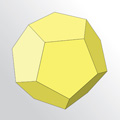
| => | 
| 
| 
| 
| 
|
Из икосаэдра: Усечённый икосаэдр

| => | 
|