Основные теоретические положения.

 

Если на вход электрической цепи с последовательно соединенными активным сопротивлением R, индуктивностью L и емкостью С (рис. 3.1) подается подать переменное синусоидальное напряжение ,

 

 

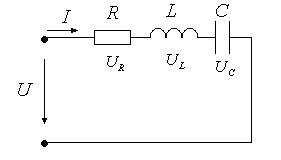Рис.3.1.

 

комплексное значение которого

,

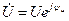то по цепи будет протекать ток

,

 

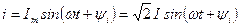комплексное значение которого

.

Согласно второму закону Кирхгофа в комплексной форме записи напряжение, подводимое к этой электрической цепи, может быть записано

,

где 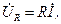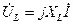, - комплексные напряжения на участках цепи.

Причем X_L=ωL и Х_с=1/ωС -индуктивное и емкостное сопротивления; ω=2πf - угловая частота; f - частота напряжения.

Если комплексы напряжений активного, индуктивного и емкостного участков цепи заменить произведениями комплексов тока и сопротивления, то уравнение для подводимого к электрической цепи комплексного напряжения преобразуется к виду

 

 

или к виду уравнения, записанного в комплексной форме по закону Ома для всей цепи: ,

где - полное комплексное сопротивление электрической цепи переменного тока.

Модуль полного комплексного сопротивления цепи переменного тока

,

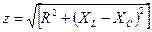а аргумент

,

 

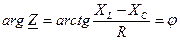есть угол между векторами напряжения и тока, определяемый как разность начальных фаз соответственно

 

.

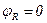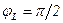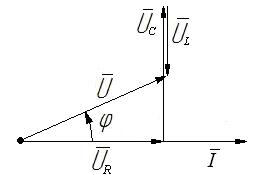
С учетом того, что на резисторе R напряжение совпадает по фазе с током ( ), на индуктивности L напряжение опережает ток на угол ( ), а на емкости С напряжение отстает от тока на ( 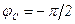), построенная векторная диаграмма для электрической цепи (рис. 3.1) представлена на рис. 3.2.

 

 

 

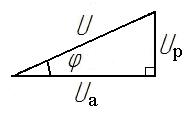Рис. 3.2.

 

Взаимосвязь между действующими значениями тока и напряжения и полным сопротивлением цепи определяется соотношениями

 

U=zI или I=U/z,

 

где действующие значения напряжения 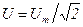и тока .

 

Из треугольника напряжений на векторной диаграмме (рис. 3.2), можно получить треугольник сопротивлений (рис. 3.3) для рассматриваемой цепи, разделив стороны этого треугольника на комплексный ток 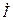, из которого следует, что ;

 

,

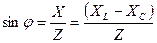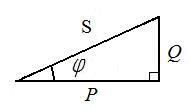
а также треугольник мощностей (рис. 3.4), умножив стороны треугольника сопротивлений на квадрат тока в цепи I².

 

 

 

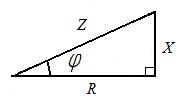Рис. 3.3. Рис. 3.4.

 

Активная мощность цепи переменного тока

 

,

 

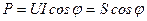отсюда .

Из треугольника мощностей можно установить взаимосвязь между активной Р, полной S и реактивной Q мощностями электрической цепи:

 

,

,

.

 

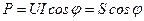При этом реактивная составляющая полной мощности цепи находится как разность реактивной индуктивной Q_L. и реактивной емкостной Q_C составляющих:

.

Выражения для полной мощности цепи переменного тока в комплексной форме записывают в следующем виде:

 

или

,

где - сопряженное значение комплексного тока .

 

Полученные выражения показывают, что угол сдвига фаз между током 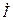и напряжением питающей сети зависит от характера сопротивлений, включенных в цепь переменного тока. При этом если

 

, т.е. – характер нагрузки индуктивный,

, т.е. – характер нагрузки емкостной.

 

Однако возможно особое состояние цепи переменного тока при последовательном включении активного сопротивления R, индуктивности L и емкости С, при котором индуктивное сопротивление цепи равно емкостному сопротивлению .

, т.е. - характер нагрузки чисто активный.

Это явление в неразветвленной электрической цепи переменного тока называется резонансом напряжений.

Условием для возникновения резонанса является равенство реактивных сопротивлений и равенство нулю разности фаз тока и напряжения на входе цепи . Частота, на которой возникнет равенство реактивных сопротивлений, называется резонансной и определяется как .

В простейшем случае резонанс напряжений может быть получен в электрической цепи при последовательном включении катушки индуктивности и конденсаторов за счет изменения емкости конденсаторов при постоянных параметрах катушки. Значения частоты, индуктивности, напряжения и активного сопротивления цепи неизменны. Векторная диаграмма тока и напряжений этой цепи при резонансе представлена на рис. 3.5.

 

Рис. 3.5.

 

Реактивная составляющая напряжения U_L. на катушке при резонансе равна напряжению U_С на конденсаторе, напряжение источника U приложено к активному сопротивлению R. Точка резонанса в этих условиях определяется по наибольшему значению тока в электрической цепи.

Для резонанса напряжений характерно:

1. Полное сопротивление электрической цепи переменного тока минимально и равно ее активному сопротивлению, т.е. , так как X_L = X_С.

2. При неизменном напряжении питающей сети (U=const) ток в цепи достигает наибольшего значения I=U/z=U/R.

3. Коэффициент мощности cos φ=cos(ψ_u–ψ_i)=P/S=R/z=R/R=1, т.е. максимальный, (соответствующий ). Это значит, что вектор тока 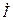и вектор напряжения сети совпадают по направлению, т.к. имеют равные начальные фазы ψ_i = ψ_u .

4. Активная мощность имеет наибольшее значение, равное полной мощности S, а реактивная мощность цепи равна нулю .

Однако реактивная индуктивная и реактивная емкостная составляющие полной мощности могут приобретать большие значения, в зависимости от значений тока и реактивных сопротивлений.

5. Напряжения на емкости и индуктивности равны и в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети.

6. Напряжение на активном сопротивлении равно напряжению питающей сети, т.е. .

При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и перенапряжения на отдельных ее участках. Поэтому, резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, т.к. может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов. В то же время резонанс напряжений широко используется в радиотехнике и электронике для выделения сигналов заданной частоты.