Комплексное изображение синусоидального тока.
Комплексное представление синусоидальных токов и напряжений позволяет совместить простоту и наглядность векторного представления с точностью представления действительными функциями времени. Для перехода от графического к комплексному представлению, заменим оси декартовой системы координат (рис.2.2) следующим образом:
-ось Х на ось действительных чисел Re;
-ось Y на ось мнимых чисел Jm (рис.2.4).
При этом длина вектора тока (напряжения) по-прежнему определяется амплитудным значением, но обозначается как комплексная величина, т.е. 
. Угол наклона вектора к оси реальных чисел Re в момент времени t=0 остается прежним, т.е. j.
Обозначим проекцию вектора 
на ось 
реальных чисел i/ = Im×cosj, а проекцию на ось мнимых чисел 
= Im× sin j. Тогда очевидно, что:
, (2.5)
где j - мнимая единица, причем 
- 
Выражение (2.5) определяет комплексную алгебраическую форму представления синусоидального тока. Она удобна для выполнения действий сложения и вычитания токов (напряжений).
Действительно, для сложения двух комплексных чисел достаточно отдельно сложить действительные и мнимые числа.
Подставим в (2.5) вместо 
и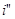 
их значения. Тогда получим:
İ 
, (2.6)
где 
- модуль комплексного представления тока, численно равный амплитудному значению.
Выражение (2.6) определяет комплексную тригонометрическую форму представления синусоидального тока. Из рис. 2.4 очевидно, что:
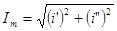, а 
. (2.7)
Видим, что выражения (2.7) характеризуют параметры синусоидального тока, не зависящие от времени - действительную амплитуду и начальную фазу j. Они позволяют легко перейти от комплексной формы представления к представлению действительными функциями времени.
Введем в (2.5) зависимость от времени. Тогда:
İ 
, (2.8)
где 
Теперь очевидно, что реальная часть (2.8) характеризует реально существующее колебание, описываемое действительной косинусной функцией, мнимая часть - это же колебание в синусной форме.
С помощью формулы Эйлера от (2.6) переходят к показательной форме комплексного представления тока:
İ 
, (2.9)
а с учетом зависимости от времени:
İm 
İm 
. (2.10)
Комплексная показательная форма удобна для выполнения действий умножения, деления, возведения в степень или извлечения корня. Действительно, для умножения двух комплексных чисел в показательной форме (2.9) достаточно перемножить их модули, а аргументы (показатели степени) сложить.
Представим токи и напряжения на пассивных элементах, обладающих активным сопротивлением, емкостью и индуктивностью в комплексной форме. Пусть имеем:
İ 
İ 
; 
Для элемента с активным сопротивлением справедливо равенство:
.
Перепишем это равенство в показательной форме:
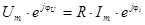(2.11)
Но равенство (2.11) возможно только в том случае, когда 
. Таким образом, мы пришли к важному выводу о том, что на элементе с активным сопротивлением ток и напряжение совпадают по фазе, т.е. максимумы тока и напряжения имеют место в один и тот же момент времени, Векторы тока и напряжения будут совпадать (рис. 2.5).
Для элемента обладающего емкостью известно выражение:
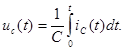
Применяя к нему комплексную форму представления тока и напряжения получим:
.
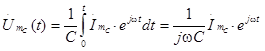Учитывая, что 
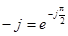приходим к выражению:
,
или:
Таким образом, видим, что напряжение на емкости отстает от тока на 90о (см. рис.2,6)
Для элемента, обладающего индуктивностью, воспользуемся выражением (1.11). Тогда:
или:
(2.13)
Видим, что напряжение на индуктивности опережает ток на 90о (см. рис. 2.7).
В заключение лекции отметим что выражения (2.11), (2.12) и (2.13) не имеют временных зависимостей. Это упрощает расчеты электрических цепей, сводя их к алгебраическим операциям с комплексными числами. Именно поэтому комплексное представление широко используется при анализе электрических цепей переменного тока.