Вывод законов Ома и Джоуля—Ленца в классической электронной теории
Важнейшей задачей классической электронной теории проводимости металлов является теоретический вывод основных законов электрического тока - законов Ома и Джоуля-Ленца, установленных опытным путем. Рассмотрим вывод этих законов.
1. Предположим, что при соударениях с узлами кристаллической решетки электроны полностью теряют скорость упорядоченного движения, которую они приобретают под действием внешнего электрического поля за время t свободного пробега. В процессе свободного пробега электроны движутся равноускоренно. Поэтому средняя скорость упорядоченного движения электронов равна:
где 
макс—среднее значение максимальной скорости, приобретаемой электроном под действием электрического поля за время свободного пробега.
Пусть т—масса электрона, е—его заряд и Е—напряженность стационарного электрического поля в проводнике. Тогда уравнение движения электрона имеет следующий вид
Интегрируя это уравнение по v от 0 до vмакс и по t от 0 до t(t - средняя продолжительность свободного пробега электрона), получаем:
(20.24)
и
. (20.25)
Среднее время свободного пробега электронов можно выразить через среднюю длину свободного пробега 
и среднюю скорость движения электронов относительно кристаллической решетки проводника. Эта скорость равна сумме средней скорости их теплового движения и средней скорости и упорядоченного движения. Поэтому
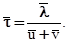
Выше было показано, что 
. Поэтому в предыдущей формуле величиной по сравнению с 
можно пренебречь 
Подставим значение 
в формулу (20.25):
(20.25`)
Заменив в (20.24) его выражением из(20.25`), получим:
. (20.26)
Величина
называетсяудельной электропроводностью, а обратная ей величина 
- удельным сопротивлением проводника.
Следовательно,
(20.27)
Формула (20.27) совпадает с (20.12) и выражаетзакон Ома в дифференциальной форме для плотности тока:
плотность тока в проводнике равна произведению удельной проводимости проводника на напряженность электрического поля.
Векторы Е и j имеют одинаковое направление. Поэтому закон Ома можно записать также в векторной форме (20.12).
2. Рассмотрим превращение энергии, происходящее при соударениях электронов проводимости с узлами кристаллической решетки. В конце свободного пробега каждый электрон теряет скорость упорядоченного движения. Средняя энергия, передаваемая при этом электроном тому иону, с которым он столкнулся, равна 
. За единицу времени электрон в среднем претерпевает 
столкновений с узлами решетки, причем
(20.28)
Все по электронов проводимости, находящихся в единице объема проводника, испытывают 
столкновений в единицу времени и передают узлам решетки металла энергию, которая идет на увеличение теплового движения ионов металла, т. е. на нагревание проводника
(20.29)
Подставив в (20.29) выражения для из (20.28) и 
из (20.24), получим величину энергии, которая передается ионам решетки в единице объема проводника за единицу времени:
(20.30)
Эта величина по своему физическому смыслу являетсяплотностью тепловой мощности тока,рассмотренная нами в уравнении (20.17).
Коэффициент есть не что иное, как удельная электропроводность
металла, поэтому (20.30) можно записать в следующем виде:
. (20.31)
Формула (20.31) представляет математическое выражениезакона Джоуля—Ленца для плотности тепловой мощности тока:
плотность тепловой мощности тока в проводнике равна произведению его удельной электропроводности на квадрат напряженности электрического поля,
и совпадает с ранее полученным выражением (20.19) дифференциальной формы закона.
В приведенных выше выводах законов Ома и Джоуля—Ленца мы предполагали, что при соударениях электронов с узлами кристаллической решетки электроны полностью теряют скорость упорядоченного движения. Г. Лоренц показал, что это предположение несущественно. К тем же результатам можно прийти, считая, что соударения электронов с узлами решетки являются абсолютно упругими.