ПРОГРАММИРОВАНИИ

Рассмотрим две задачи линейного программирования:

 

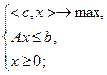(2.3.1)

 

(2.3.2)

 

где , , 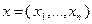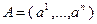– матрица размерности , , ; .

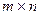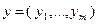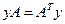Задача (2.3.2) называется двойственной к задаче (2.3.1). Покажем, что задача (2.3.1) является двойственной к задаче (2.3.2). Задаче (2.3.2) эквивалентна задача

 

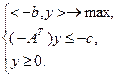(2.3.3)

 

Запишем задачу, двойственную к (2.3.3):

 

 

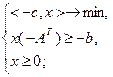
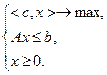
Таким образом, задачи (2.3.1) и (2.3.2) обе являются двойственными, т.е. каждая из них двойственна другой.

Пример 2.3.1

 

Исходная задача: Двойственная задача:

 

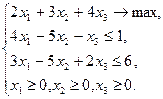
Здесь , , .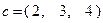

 

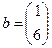В дальнейшем, когда это удобно, допустимые множества задач (2.3.1) и (2.3.2) будем обозначать через и :

 

 

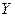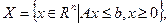
Некоторые важные свойства двойственных задач устанавливают следующие теоремы.

 

Теорема 2.3.1

 

 

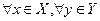
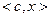
Доказательство. Поскольку и , справедливо неравенство 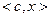. Преобразуем его правую часть и оценим ее сверху:

 

 

Неравенство в полученном выражении справедливо в силу того, что и . Из полученного результата следует 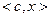Теорема доказана.

 

Следствие. Если , и , то 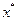– решение задачи (2.3.1), – решение задачи (2.3.2). Действительно, в силу доказанной теоремы

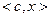
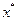в точке достигается максимум;

в точке достигается минимум.

 

Для следующих двух теорем приведем только формулировки.

 

Теорема 2.3.2 (первая теорема двойственности)

 

Задача (2.3.1) имеет решение тогда и только тогда, когда задача (2.3.2) имеет решение. При этом , где 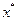– решение задачи (2.3.1), – решение задачи (2.3.2).

Теорема 2.3.3 (вторая теорема двойственности)

 

1). Если допустимые множества задач (2.3.1) и (2.3.2) не пусты, то каждая из них имеет решение.

2). Если , , то в задаче (2.3.1) .

3). Если , , то в задаче (2.3.2) .

 

Следствие. Если и целевая функция задачи (2.3.1) ограничена на множестве сверху, т.е. ( ), то задача (2.3.1) имеет решение и, следовательно, задача (2.3.2) также имеет решение.

Если и целевая функция задачи (2.3.2) ограничена на множестве 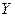снизу, т.е. ( ), то задача (2.3.2) имеет решение и, следовательно, задача (2.3.1) также имеет решение.

 

Теорема 2.3.4

 

Точки , являются решениями задач (2.3.1) и (2.3.2) соответственно тогда и только тогда, когда выполнены равенства

 

(2.3.4)

 

(2.3.5)

 

Доказательство. Пусть точки и являются решениями задач (2.3.1) и (2.3.2) соответственно. Тогда имеют место соотношения:

 

(2.3.6)

 

Согласно теореме 2.3.2, Поэтому неравенства в (2.3.6) могут быть заменены на равенства:

 

= = (2.3.7)

 

Используя (2.3.7), запишем:

 

= (2.3.8)

 

Поскольку в силу ограничений задач (2.3.1) и (2.3.2)

 

 

из (2.3.8) следует

 

 

Формулы (2.3.5) выводятся аналогично. Воспользовавшись выражением (2.3.7), запишем:

 

= (2.3.9)

 

В силу ограничений задач (2.3.1) и (2.3.2):

 

 

С учетом этого из (2.3.9) следует

 

 

Для доказательства теоремы в обратную сторону предположим, что в некоторых точках и выполнены равенства (2.3.4), (2.3.5). Докажем, что эти точки оптимальны. В силу сделанного предположения, из (2.3.8), (2.3.9) и (2.3.7) следует:

 

 

На основании первой теоремы двойственности (теорема 2.3.2) заключаем, что 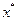и – решения задач (2.3.1) и (2.3.2), т.е. точк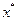и и оптимальны. Теорема доказана.

 

Теория двойственности применяется:

1) для выяснения оптимальности точек (если в точках и имеет место равенство , то эти точки оптимальны);

2) в тех случаях, когда рассмотрение двойственной задачи облегчает получение решения.

 

Рассматривая ограничения задач (2.3.1) и (2.3.2), запишем:

(2.3.10)

 

(2.3.11)

 

Пусть – решение задачи (2.3.1) и при некотором выполнено неравенство . Тогда из (2.3.4) следует, что -е ограничение в (2.3.11) на решении двойственной задачи (2.3.2) должно выполняться как равенство:

 

(2.3.12)

 

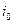Если при некотором соответствующее ( -е) ограничение в (2.3.10) на решении 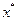задачи (2.3.1) выполнено как строгое неравенство, т.е. если

 

(2.3.13)

 

то из (2.3.5) следует, что в решении задачи (2.3.2) . Использование выражений (2.3.12) и (2.3.13) в контексте приведенных рассуждений позволяет по найденному решению одной из двойственных задач определить решение другой.

Равенства (2.3.4) и (2.3.5) называются условиями равновесия (дополняющей нежесткости). Ограничения называются выполненными нежестко, если в ограничениях имеет место строгое неравенство.

 

Пример 2.3.2

 

(2.3.14)

 

Требуется найти решение данной задачи, затем сформулировать и решить двойственную задачу.

Для решения задачи (2.3.14) воспользуемся геометрическим методом. Иллюстрация геометрического решения представлена на рис. 2.3.1. Следуя рассуждениям, аналогичным сделанным при решении задачи из примера 2.1.2, приходим к выводу о том, что решением задачи (2.3.14) является точка . Сформулируем задачу, двойственную к задаче (2.3.14):

 

(2.3.15)

Поскольку , , в соответствии с (2.3.12) второе и третье неравенства в (2.3.15) на решении этой задачи должны выполняться как равенства:

(2.3.16)

 

Первое ограничение задачи (2.3.14) выполнено на ее решении как строгое неравенство:

 

 

Поэтому, в соответствии с рассуждениями, сделанными при рассмотрении выражения (2.3.13), Учитывая это, из системы, составленной из уравнений (2.3.16), находим: ; . Таким образом, решением задачи (2.3.15) является Нетрудно убедиться в том, что , как это и должно быть в соответствии с теоремой 2.3.2.

 

Пример 2.3.3

 

(2.3.17)

 

Для решения данной задачи удобно сначала сформулировать и решить двойственную задачу:

 

(2.3.18)

 

Графическое (геометрическое) решение задачи (2.3.18) представлено на рис. 2.3.2. В результате получаем оптимальную точку . Подстановка найденных значений и в ограничения задачи (2.3.18) позволяет установить, что второе и третье ограничения выполняются как строгие неравенства. Это означает, что в решении исходной задачи (2.3.17) , . Поскольку и , первые два ограничения задачи (2.3.17) на ее решении должны выполняться как равенства. Поэтому с учетом найденных значений , получаем систему уравнений, решением которой являются значения и :

 

 

, .

 

Таким образом, оптимальная точка задачи (2.3.17) . Значение целевой функции задачи (2.3.17) или целевой функции задачи (2.3.18) в найденных для каждой задачи оптимальных точках составляет . Использование двойственной задачи с меньшим числом переменных позволило упростить получение результата.

Пример 2.3.4 (специальная задача)

(2.3.19)

 

Сформулируем задачу, двойственную к (2.3.19):

 

(2.3.20)

 

Предположим, что найдено решение задачи (2.3.20): . Нетрудно видеть, что первые ограничений этой задачи, за исключением самого первого ограничения, на решении всегда будут выполнены как строгие неравенства. Поэтому оптимальная точка задачи (2.3.19) будет иметь нулевые значения всех координат, кроме первой. При этом первая координата решения задачи (2.3.19) принимает значение, равное , так как именно в этом случае при указанных условиях целевая функция рассматриваемой задачи принимает минимальное значение (также равное ). Итак, .

Наряду с рассмотренными ранее, находит применение общая постановка задачи линейного программирования:

 

(2.3.21)

 

(2.3.22)

 

Задачи (2.3.21) и (2.3.22) являются двойственными друг по отношению к другу. На переменные и не наложено условие их неотрицательности, так как они являются избыточными и могут быть исключены из задач (2.3.21) и (2.3.22) с помощью уравнений, присутствующих в ограничениях. Для записи двойственных задач линейного программирования в общей постановке можно использовать таблицу вида табл. 2.3.1. Здесь при записи ограничений задачи (2.3.21) подразумевается формирование сумм произведе-

 

Таблица 2.3.1

 

			…			…
			…			…
			…			…
…	…	…	…	…	…	…	…	…	…
			…			…
			…			…		=
…	…	…	…	…	…	…	…	…	…
			…			…		=
			…		=	…	=
			…			…

 

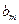
ний переменных , на соответствующие элементы матрицы при движении по ее строкам. При записи ограничений задачи (2.3.22) осуществляется формирование сумм произведений переменных , 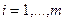на соответствующие элементы матрицы при движении по ее столбцам.

 

Пример 2.3.5. Для данной задачи сформулировать двойственную:

 

 

В данном случае рассмотренная выше таблица имеет вид:

 

		-1			1
			-1	=	6
			=
	1	4	2

 

Двойственная задача формулируется следующим образом: