Сложное движение точки
Рассмотрим движущееся тело А (рис. 2.36) и точку М, не принадлежащую этому телу, а совершающую по отношению к нему некоторое движение. Тело перемещается относительно неподвижной системы координат O1х1y1z1. С телом неизменно связана система координат Oxyz, которая перемещается вместе с телом, поэтому в дальнейшем будем называть ее подвижной системой координат. Движение точки можно рассматривать одновременно как по отношению к подвижной, так и по отношению к неподвижной системам координат. Движение, совершаемое при этом точкой, называют сложным. Например, сложное движение совершает лодка, переплывающая реку, пассажир, перемещающийся в вагоне движущегося поезда.
Рис. 2.26
Движение точки относительно неподвижной системы координат O1х1y1z1 называется абсолютным или сложным. Скорость и ускорение точки относительно неподвижной системы координат соответственно будем называть абсолютными и к символу скорости и ускорения добавлять индекс по названию точки. Например, для точки М – 
M, 
M. Иногда, если исследуется движение одной точки, индекс опускается и пишется просто , .
Движение точки относительно подвижной системы координат Oxyz будем называть относительным. Скорость и ускорение точки относительно подвижной системы координат называют соответственно относительной скоростью и относительным ускорением, и к символам скорости и ускорения добавляется индекс по названию точки и индекс «r». Например, для точки М – Mr, Mr - Но иногда, если исследуется движение одной точки, в индексе название точки опускается и пишется просто r, r.
Движение подвижной системы координат Oxyz относительно неподвижной O1х1y1z1 называется переносным. Переносными скоростью и
ускорением называются соответственно скорость и ускорение относительно неподвижной системы координат O1х1y1z1 той точки подвижного тела, в которой в данный момент находится подвижная точка. При обозначении переносных скорости и ускорения к символам скорости и ускорения добавляется индекс по названию точки и индекс «е». Например, для точки М - Me, Me. Иногда, если в задаче исследуется движение одной точки, индекс, соответствующий наименованию точки, опускается и пишется просто e, e.
Связь между абсолютной, относительной и переносной скоростями точки показана в теореме о сложении скоростей точки при сложном движении, согласно которой абсолютная скорость точки, совершающей сложное движение, равна геометрической сумме относительной и переносной скоростей:
= r+ e. (2.57)
Для определения абсолютной величины одного из членов, входящих в уравнение (2.57), можно использовать какой-либо известный метод сложения векторов, например, метод треугольника или проекций.
Согласно теореме о сложении ускорений при сложном движении материальной точки (теорема Кориолиса) абсолютное ускорение точки равно геометрической сумме относительного ускорения, переносного ускорения и ускорения Кориолиса:
= r+ e + k. (2.58)
Ускорение Кориолиса определяется векторным произведением:
(2.59)
где 
e – вектор переносной угловой скорости (угловая скорость подвижной системы координат).
Модуль ускорения Кориолиса будет равен
(2.60)
где sin( 
e, r) – синус угла между векторами e, r.
Из выражения (2.60) следует, что ускорение Кориолиса равно нулю в следующих случаях:
а) ωe = 0, то есть при поступательном перемещении подвижной
системы координат;
б) 
e || r, то есть когда вектор угловой скорости подвижной системы координат параллелен вектору относительной скорости;
в) Vr =0, то есть в момент времени, в который относительная
скорость точки равна нулю.
Направление вектора ускорения Кориолиса можно определять по правилу направления вектора, получаемого в результате векторного произведения двух векторов, но удобнее воспользоваться правилом Н.Е. Жуковского, согласно которому для определения направления вектора ускорения Кориолиса необходимо вектор относительной скорости спроецировать на плоскость, перпендикулярную вектору переносной угловой скорости (оси переносного вращения), а затем повернуть на угол 90 градусов в направлении переносного вращения (рис. 2.37).
Рис. 2.37
Так как правая часть векторного уравнения (2.58) содержит, как правило, больше двух векторов, выполнение операций суммирования при решении этого уравнения удобно выполнять методом проекций. Заметим, что если переносное движение не прямолинейное поступательное, а относительное движение точки происходит по криволинейной траектории, ускорения e, r будут содержать несколько составляющих. В таких случаях вид уравнения (2.58) существенно осложняется. Так, например, если переносное движение вращательное, а относительное происходит по криволинейной траектории, уравнение (2.58) приобретает вид
= en + eτ + rn + rτ + k, (2.61)
где en , eτ – соответственно нормальная и касательная составляющие переносного ускорения; rn rτ –соответственно нормальная и касательная составляющие в относительном движении.
При решении задач на сложное движение материальной точки важно правильно указать направление векторов, входящих в уравнения (2.57), (2.58). Обычно определение направления нормальных составляющих векторов не вызывает трудностей. Для правильного определения направлений векторов скоростей и касательных составляющих ускорения обязательно предварительно определить их алгебраические величины и, соответственно, используя теорию поступательного или вращательного движения тела, выбрать направления этих векторов.
Существует большое количество задач механики, которые можно успешно решать, используя теорию сложного движения материальной точки. Несмотря на значительные различия в их условиях, решение можно производить в следующей последовательности:
а) выделить тело, движение которого является для изучаемой точки
переносным;
б) определить положение точки на теле, если оно не задано;
в) задать подвижную и неподвижную системы координат;
г) классифицировать вид переносного движения и траекторию относительного;
д) записать уравнения теорем о сложении скоростей и сложении
ускорений для исследуемой материальной точки;
е) подсчитать алгебраические величины и модули векторов, входящих в уравнения теорем о сложении скоростей и ускорений, для которых это возможно (кроме ускорения Кориолиса);
ж) указать на чертеже направление векторов, входящих в уравнения теорем о сложении скоростей и сложении ускорений, для которых это
возможно сделать (кроме направления ускорения Кориолиса);
з) подсчитать модуль и указать на чертеже направление ускорения
Кориолиса;
и) решая уравнение теоремы о сложении скоростей, найти неизвестные величины, входящие в него; решение уравнения возможно как с использованием правила треугольника, так и метода проекций;
к) проецируя уравнения теоремы о сложении ускорений на оси декартовой системы координат, найти неизвестные величины, входящие в него.
Пример 2.8. Тележка перемещается по прямолинейным направляющим по закону L = t3+ 4t см. В корпусе тележки имеется канал в форме дуги окружности радиусом R=48 см с центром в точке В. По каналу перемещается материальная точка М по закону AM = 4π· t2см. В момент времени t1 =2 с определить абсолютную скорость и абсолютное ускорение точки М (рис. 2.38).
Рис. 2.38
В этой задаче движение корпуса тележки будет переносным, движение точки относительно корпуса – относительным. Положение точки на корпусе тележки определим углом 
(рис. 2.39):
рад
Рис. 2.39
Введем неподвижную систему координат O1х1y1. Ось O1х1 направим по направляющей, по которой перемещается тележка. Ось O1y1 вверх, перпендикулярно оси O1х1. Начало координат расположим в точке направляющей, относительно которой отсчитывается перемещение тележки. Тогда
x1=L = t3 +4t.
Подвижную систему координат Оху свяжем с корпусом тележки
(рис. 2.39).
Запишем уравнение теоремы о сложении скоростей для точки М:
= e+ r. (2.62)
Записывая уравнение теоремы о сложении ускорений для точки М, учтем, что переносное движение поступательное, а траектория относительного движения криволинейная. Поэтому ускорение Кориолиса будет равно нулю, а относительное ускорение будет иметь две составляющие – нормальную rn и касательную τr .Получим
= 
e+ rn + 
τr. (2.63)
Определим алгебраические величины и модули векторов, входящих в правые части уравнений (2.62), (2.63):
см/с; 
см/с;
см/с2; 
см/с2;
см/с2
В момент времени t1 = 2с: 
e =Ve =16 см/с; r =Vr =50,27см/с;
e=We =12см/с2; rτ =Wrτ =25,13 см/с2; Wrn =52,63см/с2.
Нанесем на чертеж (рис. 2.39) все векторы, входящие в правые части уравнений (2.62), (2.63), учитывая знаки их алгебраических величин. Так как переносное движение прямолинейное поступательное, векторы e, e направим параллельно оси O1х1. Векторы r, τr направим перпендикулярно отрезку ВМ в сторону увеличения дуги AM. Вектор nr направим по отрезку ВМ от точки М к точке В – центру дуги окружности.
Из чертежа видно, что угол между векторами e и r равен 120°, поэтому для вычисления модуля абсолютной скорости используем формулу, вытекающую из теоремы косинусов, получим
см/с.
Спроецировав векторное уравнение (2.63) на оси системы координат O1х1y1 определим проекции вектора абсолютного ускорения точки М:
Wx=We- Wnr cos60° - Wτr cos30° =-35,9 см/с2;
Wy = Wnr sin60° - Wτr sin30° =33,01 см/с2.
Тогда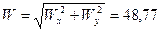 
см/с2.
Пример 2.9. Полое кольцо радиусом R=0,3 м, укрепленное на стержне ОК длиной 1=0,3 м, вращается вокруг точки О по закону
φ = 5t-4t2 рад. По каналу внутри кольца перемещается шарик М, причем длина дуги AM изменяется по закону s = AM = 0,15π· t3/8 м. В момент времени t1 =2c определить абсолютную скорость и абсолютное ускорение шарика (рис. 2.40).
В данной задаче движение кольца будет переносным и вращательным относительно точки О. Движение шарика относительно кольца будет относительным. Положение шарика относительно кольца определим углом а (рис. 2.41):
рад
Рис. 2.40
Введем в рассмотрение неподвижную декартову систему координат O1х1y1, расположенную в плоскости вращения кольца, начало которой поместим в точке О, оси координат направим произвольно. Подвижную декартову систему координат Оху свяжем с вращающимся кольцом; ее начало также расположим в точке О, ось Ох направим по стержню ОК, ось Ох перпендикулярно оси Оу (рис. 2.41).
Рис. 2.41
Запишем уравнение теоремы о сложении скоростей для точки М:
= e+ r. (2.64)
Так как переносное движение вращательное, а относительное совершается по криволинейной траектории, уравнение теоремы о сложении ускорений для точки М примет вид:
= en+ eτ + rn + rτ + k. (2.65)
Определим алгебраические величины и модули векторов, входящих в правые части уравнений (2.64), (2.65)
1/c; 
1/c2
e = OM· 
e= OM· (5 – 8t) м/с; r = ds/dt = 0,056π · t2 м/с;
e n = OM· ωe2= OM· (5 – 8t) 2 м/с; еτ = OM· 
e = - OM· 8 м/с2;
Wr n = Vr 2 /R = 0,0031π2 t4 м/с2; r τ =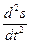 
= 0,113π · t м/с2
Учитывая, что ОМ = R√5 = 0,67 м, при t1 = 2с получим:
e =-11 1/с, e =-8 1/с2; e =-7,37 м/с; r =0,71 м/с;
We n =81,07 м/с2; eτ =-5,36 м/с2; Wr n =1,68 м/с2; r τ =0,71 м/с2.
Тогда
ωe =11 1/с, εe =8 1/с2; Ve =7,37м/с, Vr =0,71м/с; We τ =5,36м/с2;
Wr τ =0,71 м/с 2.
Учитывая знаки алгебраических величин векторов, входящих в правые части уравнений (2.64), (2.65), нанесем направления этих векторов на чертеж (рис. 2.41), на котором также изогнутой стрелкой укажем направление вращения кольца.
Модуль ускорения Кориолиса будет равен
Wk = 2Vr ωe sin90o =15,62 м/с2.
Угол между векторами r и 
e в данном случае будет равен 90°, так как вектор r лежит в плоскости, перпендикулярной оси переносного вращения, а вектор e направлен по этой оси.
Для определения направления ускорения Кориолиса воспользуемся правилом Жуковского. Так как вектор r уже лежит в плоскости, перпендикулярной оси переносного вращения, для определения
направления ускорения Кориолиса достаточно повернуть его на угол 90° в направлении переносного вращения (в данном случае по направлению вращения часовой стрелки). Нанесем направление вектора ускорения Кориолиса на чертеж (рис. 2.41).
Для проецирования векторов, входящих в правые части уравнений (2.64), (2.65) на оси системы координат Оху, определим косинус и синус угла b – угла между положительным направлением оси Ох и отрезком ОМ, получим
Проецируя уравнение (2.64) на оси системы координат Оху, найдем проекции вектора абсолютной скорости точки М на ее оси:
Vx = Ve sin β - Vr = 2,59 м/с; Vy = Ve cos β = 6,59 м/с,
по которым определим модуль абсолютной скорости:
м/с.
Проецируя уравнение (2.65) на оси подвижной системы координат Оху, найдем проекции вектора абсолютного ускорения точки М на ее оси:
Wx = - We n cos β + We τ sin β – Wr τ = -70,82 м/с2;
Wy = - We n sin β - We τ cos β - Wr n +Wk= -27,32 м/с2,
по которым затем определим модуль абсолютного ускорения
м/с2.
Пример 2.10.Кулисный механизм состоит из шатунов ОВ, О1А и ползуна (рис 2.42). Ползун шарнирно прикреплен к кривошипу ОВ и скользит по кривошипу О1А. Кривошип ОВ вращается с угловой скоростью ωO = 5 1/с и угловым ускорением εO = 10 1/с2 в направлении, указанном на рис. 2.42. Рассматривая ползун как материальную точку, совпадающую с шарниром В, определить угловую скорость и угловое ускорение кривошипа О1А и относительную скорость и относительное ускорение перемещения ползуна по кривошипу О1А, если О1В = ОВ = О1О = 1 м.
Рис. 2.42
В данной задаче вращательное движение кривошипа О1А для ползуна будет переносным, поступательное перемещение ползуна по кривошипу О1А будет относительным, а движение ползуна вместе с кривошипом ОВ относительно точки О будет абсолютным.
Введем в рассмотрение неподвижную систему координат Oх1y1, ее начало разместим в точке О, ось Oх1 проведем через точку O1, ось Оу1 -перпендикулярно оси Oх1. Начало подвижной системы координат Вху разместим в точке В, ось Вх направим по кривошипу О1А, ось By перпендикулярно оси Вх (рис. 2.43).
Так как точка В крепления ползуна и кривошипа ОВ является для них общей, а кривошип ОВ совершает вращательное движение относительно неподвижной точки О, абсолютные скорость и ускорение точки В ползуна можно определить как ускорение точки В кривошипа ОВ во вращательном движении относительно точки О.
Рис. 2.43
Запишем для точки В теорему о сложении скоростей при сложном движении:
= e+ r, (2.66)
и теорему о сложении ускорений при сложном движении. С учетом того, что абсолютное движение точки В ползуна происходит по известной нам криволинейной траектории, переносное движение вращательное, а относительное движение поступательное, уравнение теоремы о сложении ускорений для точки В примет вид:
n + τ= en+ eτ + r+ k. (2.67)
Определим модули векторов, которые мы можем определить на данном этапе решения задачи:
V = ωO · ОВ = 5 м/с; Wn = ωO 2ОВ = 25м/с2; Wτ = εO ·ОВ = 10 м/с2.
Нанесем на чертеж (рис. 2.43) векторы, входящие в уравнения (2.66),(2.67), кроме ускорения Кориолиса. Направление векторов , r, e, en, n, τ выберем с учетом заданного направления вращения кривошипа ОВ и конструкции механизма. Вектор r направим вдоль кривошипа О1А в произвольную сторону, так как нам неизвестно, ускоренно движется ползун в относительном движении или замедленно. Вектор eτ направим перпендикулярно кривошипу О1А в произвольном направлении, так как нам неизвестно, будет ли замедленным или ускоренным вращение этого кривошипа. Укажем также изогнутой стрелкой направление переносного вращения кривошипа О1А.
Используя правило Жуковского, определим направление ускорения Кориолиса. Для этого, учитывая, что вектор r уже расположен в плоскости, перпендикулярной оси переносного вращения, повернем его на
угол 90° в направлении переносного вращения.
Проецируя уравнение (2.66) на оси подвижной системы координат Вху, определим модули векторов переносной и относительной скоростей e и r:
V cos 60° = Ve; => Ve = 2,5 м/с; V sin 60° = Vr; => Vr = 4,3 м/с.
Найдем модуль угловой скорости переносного движения (кривошипа О1А):
ωe=Ve/O1B = 2,51/с.
После этого можем определить модуль нормальной составляющей переносного ускорения и модуль ускорения Кориолиса:
Wen = ωе2О1В = 6,25 м/с2; Wk = 2ωeVr sin90° = 21,5 м/с2.
Угол между векторами r и е равен 90°, так как вектор r лежит в плоскости, перпендикулярной оси переносного вращения, по которой направлен вектор е.
Спроецировав векторное уравнение (2.67) на оси подвижной системы координат Вху, получим два скалярных уравнения:
- Wncos60° + Wτ cos30° = -Wen + Wr;
- Wnsin60° - Wτ sin30° = - Weτ - Wk,
из которых определим модуль относительного ускорения ползуна и касательной составляющей ускорения точки В в переносном движении:
Wr =- Wn cos60° + Wτ cos30o +Wen =2,41 м/с2;
Weτ = Wn sin60o+ Wτ sin30o- Wk =5,15 м/с2.
Модульуглового ускорения кривошипа О1А будет равен
1/с2.
СПИСОК ЛИТЕРАТУРЫ
1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: учебник для вузов. М.: Наука, 1979. Т. 1.
2. Бухгольц Н.Н. Основной курс теоретической механики: учебник для университетов. М.: Наука, 1965. Т. 1.
3. Никитин М. М. Курс теоретической механики: учебник для вузов. М.: Высшая школа, 1990 и предыдущие издания.
4. Тарг СМ. Краткий курс теоретической механики: учебник для вузов. М.: Высшая школа, 1998 и предыдущие издания.
5. Яблонский А.А. Курс теоретической механики: учебник для вузов. М.: Высшая школа, 1984 и предыдущие издания. Т. 1.
6. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах: учеб. пособие для вузов. М.: Наука, 1990 и предыдущие издания.
7. Теоретическая механика: методические указания и контрольные задания / под ред. С.М. Тарга. М.: Высшая школа, 1989.
8. Сборник заданий для курсовых работ по теоретической механике / под ред. А.А. Яблонского. М.: Высшая школа, 1985.
ОГЛАВЛЕНИЕ
Введение...............................................................................................................3
1. Статика.............................................................................................................5
1.1. Основные понятия и определения.......................................................5
1.2. Аксиомы статики...................................................................................8
1.3. Момент силы относительно точки и оси...........................................10
1.4. Пара сил................................................................................................13
1.5. Связи, реакции связей.........................................................................14
1.6. Система сходящихся сил....................................................................18
1.7. Пространственная и плоская системы сил.......................................26
1.8. Центр тяжести тела.............................................................................45
1.9. Равновесие тел при наличии трения.................................................51
2. Кинематика....................................................................................................59
2.1. Кинематика точки..............................................................................59
2.2. Поступательное движение твердого тела........................................72
2.3. Вращательное движение твердого тела.......тела <== предыдущая
Дата добавления: 2015-04-01; просмотров: 106; Опубликованный материал нарушает авторские права?.