Контроль на выходе по модулю ЕН.01.М.06
| № п/п | Базовые определения, понятия, теоремы | Формулировки определений, понятий, теорем | Используемая форма записи |
| Определение производной функции | Производной функции  в точке х называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю: в точке х называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю:
|   
| |
| Сложная функция Производная сложной функции | Функция y=f(u) называется сложной функцией, если её аргумент u в свою очередь функция независимого аргумента, т.е. u=  Производная сложной функции равна производной заданной функции по промежуточному аргументу, умноженной на производную этого аргумента по независимой переменной
Производная сложной функции равна производной заданной функции по промежуточному аргументу, умноженной на производную этого аргумента по независимой переменной
|
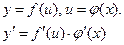
| |
| Дифференцирование обратной функции (доказательство) | Производные от взаимообратных функций обратные по величине |  от взаимообратные функции, тогда от взаимообратные функции, тогда 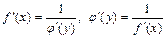
| |
| Производная функции, заданной параметрическими уравнениями | Если функция задана параметрическими уравнениями
 то её производная равна отношению то её производная равна отношению 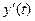 к к 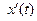
| 
| |
| Производные высших порядков | Производной n- го порядка  называется производная от производной называется производная от производной  -го порядка -го порядка
| 
| |
| Определение дифференци-руемости функции (вывод) |
Функция 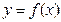 называется дифференцируемой в точке называется дифференцируемой в точке  , если её приращение можно представить равенством , если её приращение можно представить равенством 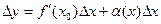
| 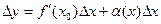
| |
| Определение дифференциала функции | Дифференциалом функции 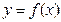 , называется главная часть приращения функции пропорциональная приращению независимой переменной ( , называется главная часть приращения функции пропорциональная приращению независимой переменной (  ) )
|  
| |
| Правило вычисления дифференциала функции | Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной |  
| |
| Правило Лопиталя | Если при х 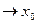 обе функции стремятся к 0 или к обе функции стремятся к 0 или к  ,
т.е. ,
т.е.  или или 
| 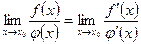
| |
| Производные основных элементарных функций | С доказательством | Таблица производных | |
| Правила дифференцирования | |||
| Суммы функций (с доказательством) | |||
| Произведения функций (с доказательством) | |||
| Частного функций | |||
| Определение касательной к графику функции | Касательной М0Т к линии АВ в её точке М0 (рис.1) называется предельное положение секущей, проходящей через точку М0 и другую точку М линии при  по линии АВ. по линии АВ.
| ||
| Геометрический смысл производной (вывод) | Значение производной функции  в точке в точке  : : 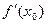 - равно угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой равной - равно угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой равной 
|

| |
| Уравнение касательной | 
| ||
| Определение нормали к графику функции | Прямая перпендикулярная касательной к кривой, проведенная в точке касания называетсянормалью к кривой | ||
| Уравнение нормали | 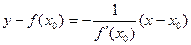
| ||
| Теорема Ферма (с доказательством) | Если функция  , непрерывная в замкнутом интервале , непрерывная в замкнутом интервале  , принимает свое наибольшее (или наименьшее) значение во внутренней точке , принимает свое наибольшее (или наименьшее) значение во внутренней точке  этого интервала: этого интервала:  . Если в точке . Если в точке  производнаяфункции производнаяфункции 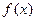 существует, то она обязательно равна нулю: существует, то она обязательно равна нулю: 
| ||
| Теорема Ролля (с доказательством) | Если функция  , непрерывна в замкнутом интервале , непрерывна в замкнутом интервале  , дифференцируема во всех её внутренних точках и имеет на концах равные значения, то внутри этого интервала существует хотя бы одно значение , дифференцируема во всех её внутренних точках и имеет на концах равные значения, то внутри этого интервала существует хотя бы одно значение  для которого для которого 
| ||
| Теорема Лагранжа (с доказательством) | Если функция 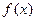 непрерывна в замкнутом интервале непрерывна в замкнутом интервале  ,дифференцируема во всех её внутренних точках, то внутри интервала существует хотя бы одно значение ,дифференцируема во всех её внутренних точках, то внутри интервала существует хотя бы одно значение  для которого для которого 
| ||
| Необходимый признак монотонности (с доказательством) | |||
| Достаточный признак монотонности (с доказательством) | |||
| Необходимый признак экстремума (с доказательством) | |||
| Достаточный признак экстремума (с доказательством) | |||
| Определения: | |||
| точек экстремума | Точки, разделяющие промежутки монотонности, называются точками экстремума | ||
| точки максимума | Точка x0 называется точкой максимумафункции  , если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие: , если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие:

| ||
| точки минимума | Точка x0 называется точкой минимумафункции  , если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие: , если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие:
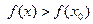
| ||
| точки перегиба | Точкой перегиба называется такая точка линии , которая отделяет выпуклую дугу от вогнутой | ||
| асимптоты графика функции | Прямая l называется асимптотой линии, если расстояние от точки линии до прямой l стремиться к нулю при неограниченном удалении этой точки от начала координат | ||
| наклонной асимптоты | Прямая 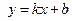 называется наклонной асимптотой графика функции называется наклонной асимптотой графика функции  при при  , если , если 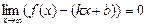
| ||
| вертикальной асимптоты | Прямая 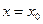 называется вертикальной асимптотой графика функции называется вертикальной асимптотой графика функции  , если хотя бы один из односторонних пределов при , если хотя бы один из односторонних пределов при  равен равен  . .
| ||
Уравнение наклонной асимптоты, формулы вычисления 
|  , , 
|