Ряд Фурье. Интеграл Фурье
Пусть f(t) – действительная периодическая функция с периодом T, для которой существует интеграл 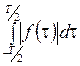 . Тогда эту функцию можно представить в виде:
. Тогда эту функцию можно представить в виде:
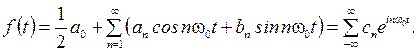 (1.3)
(1.3)
Представление (1.3) называется разложением в ряд Фурье.
Здесь:
-  - циклическая частота основного тона (первой гармоники);
- циклическая частота основного тона (первой гармоники);
- 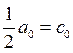 - среднее значение f(t);
- среднее значение f(t);
- члены ряда называются гармониками (n = 1 – первая гармоника или основной тон, n = 2, 3, … - обертоны).
Коэффициенты ряда определяются выражениями:

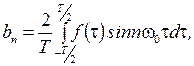

n-я гармоника имеет частоту 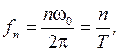 амплитуду
амплитуду 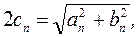 фазу
фазу 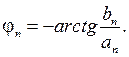
Если функция f(t) непериодическая, то ее можно представить в виде интеграла Фурье:
 (1.4)
(1.4)
