Взаимное положение точки и плоскости

Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей этой плоскости. Если это условие не выполняется, то точка находится вне пределов плоскости, т. е. при использовании системы плоскостей проекций П₁, П₂ точка может лежать перед или дальше, над или под плоскостью. Рассмотрим несколько примеров на рис. 1.44, где на комплексном чертеже задана Т( ) – восходящая плоскость.

1. Точка А принадлежит плоскости Т, т. к. проекции точки А принадлежат одноименным проекциям прямой m, которая в свою очередь принадлежит плоскости Т :

.

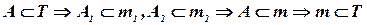2. Очевидно, что точка В не принадлежит плоскости Т, т. к. ее проекции принадлежат не одноименным проекциям прямых m и n.

3. Точка , т. к. она принадлежит вспомогательной прямой 12, которая построена принадлежащей плоскости Т.

4. Точки M и D , а точки N и E, находящиеся с ними попарно в проекционных связях, располагаются следующим образом:

- точка N находится выше точки M, т. е. над плоскостью Т;

- точка E находится ближе точки D, т. е. перед плоскостью Т.

В заключении решим обратную позиционную задачу. Определить положение точек M и N относительно плоскости Т(l,A) (рис. 1.45).

В первом случае сначала необходимо провести вспомогательную прямую А1 фронтально или горизонтально конкурирующую с точкой М и принадлежащую плоскости Т. Так как проекции точки М принадлежат одноименным проекциям прямой А1, то она принадлежит плоскости Т.

Во втором случае необходимо провести вспомогательную прямую А2, фронтально конкурирующую с точкой N и принадлежащую плоскости Т. Точка N находится перед фронтально конкурирующей с ней точкой (на рис. 1.45 помечена х) принадлежащей прямой А2, следовательно также принадлежащей плоскости Т, а значит, и перед самой плоскостью Т.