Взаимное положение прямой и плоскости
Прямая может пересекаться с плоскостью, быть параллельной плоскости или принадлежать ей. Если прямая l пересекается, параллельна или принадлежит плоскости Т, то вместе с тем она будет соответственно пересекаться (рис. 1.38), совпадать (рис. 1.39) или будет параллельна прямой b, принадлежащей этой плоскости (рис. 1.40). Справедливы и обратные положения.
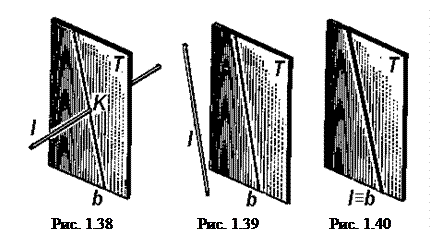 Таким образом, чтобы определить взаимное положение прямой l и плоскости Т, нужно построить вспомогательную прямую b, конкурирующую с прямой l и принадлежащую плоскости Т. Если прямые l и b пересекаются в некоторой точке К, то в этой точке прямая l пересекается с плоскостью. Если же прямые l и b совпадают или параллельны, то прямая l соответственно принадлежит или параллельна плоскости Т.
Таким образом, чтобы определить взаимное положение прямой l и плоскости Т, нужно построить вспомогательную прямую b, конкурирующую с прямой l и принадлежащую плоскости Т. Если прямые l и b пересекаются в некоторой точке К, то в этой точке прямая l пересекается с плоскостью. Если же прямые l и b совпадают или параллельны, то прямая l соответственно принадлежит или параллельна плоскости Т.
Рассмотрим примеры. На рис. 1.41, 1.42 и 1.43 изображены комплексные чертежи прямой l и Т(АВС) – нисходящая плоскость. Определим взаимное положение этих объектов.
 Построим вспомогательную прямую b, горизонтально конкурирующую с прямой l и принадлежащую плоскости Т. С этой целью на прямых АВ и ВС, которые задают плоскость Т, выделим точки 1 и 2, горизонтально конкурирующие с прямой l.
Построим вспомогательную прямую b, горизонтально конкурирующую с прямой l и принадлежащую плоскости Т. С этой целью на прямых АВ и ВС, которые задают плоскость Т, выделим точки 1 и 2, горизонтально конкурирующие с прямой l.
Первоначально с этой целью определим горизонтальные проекции 11 и 21 точек пересечения прямых АВ и ВС, которые задают плоскость Т, с прямой l. После этого, используя линии проекционных связей по принадлежности к линиям АВ и ВС, найдем фронтальные проекции точек 12 и 22.
Точки 1 и 2 задают прямую b, которая принадлежит плоскости Т и горизонтально конкурирует с прямой l. Теперь можно определить относительное положение прямых l и b.
По полю проекций П2 (рис 1.41) видно, что прямые l и b пересекаются в точке К (при этом сначала определяется ее фронтальная проекция К2, а затем горизонтальная проекция К1 (рис. 1.41). Точка К будет также точкой пересечения прямой l с плоскостью Т.
Если же при построении вспомогательной прямой b окажется, что прямая l параллельна прямой b (рис. 1.42), то это условие совместно с условием  означает, что
означает, что  и, значит, прямая l параллельна плоскости Т.
и, значит, прямая l параллельна плоскости Т.
Если же в результате построения вспомогательной прямой b окажется, что 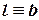 (
(  и
и 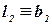 ) (рис. 1.43), то прямая l принадлежит плоскости Т.
) (рис. 1.43), то прямая l принадлежит плоскости Т.