Задача 1. Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Каток для раскатывания асфальта (рис. 1) состо­ит из кузова массой т₁ = 3∙103 кг и двух одинаковых барабанов. Масса барабана m₂=103 кг, радиус его r=0,5м, а радиус инерции ρ=0,4м. Коэффициент трения каче­ния барабанов f_к=9 см. Определить скорость кузова катка после того, как он проехал расстояние S=2 м, начальная скорость катка была равна 0,2 м/с. К ведущему барабану приложен постоянный момент M=4,6 кНм.

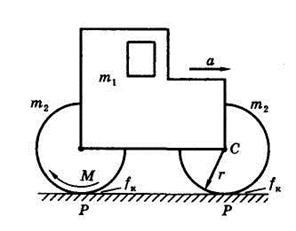
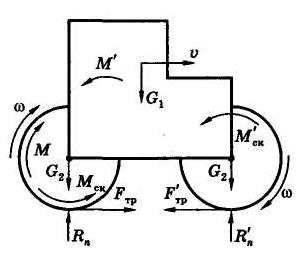
Рис. 1 Рис. 2

 

Решение. Так как в задаче идет речь о конечном перемещении системы, то следует применить теорему об изменении кинетической энергии в интегральной (конечной) форме:

 

.

 

 

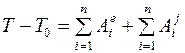Кинетическая энергия системы (поступательно движу­щийся кузов и совершающие плоское движение бараба­ны) имеет вид

 

,

 

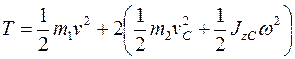где v — скорость кузова, v_С — скорость центра масс бара­бана, ω — его угловая скорость, J_zC = m₂ρ² = 160 кгм² — момент инерции барабана относительно его оси (проходя­щей через центр масс).

Кинематические связи определяются тем, что каждый барабан поворачивается вокруг своего мгновенного центра скоростей (точки Р), а именно: v_C = ωr; кроме того, v = v_C, т. е. ω = v/r. Тогда кинетическая энергия приводится к виду

,

 

 

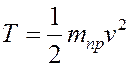где т_пр= 6280 кг — приведенная к кузову масса системы. Начальная кинетическая энергия системы

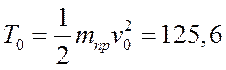Дж.

 

Вычислим теперь величину работы действующих сил (рис. 2).

Внешние силы. Силы тяжести барабанов G₂ и кузова G₁ работы не совершают, поскольку они перпендикуляр­ны скоростям (и, соответственно, перемещениям) точек их приложения. Также не работают нормальные реакции R_n и R’_n и силы трения F_rp и 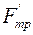, так как всегда равны нулю скорости их точек приложения — мгновенных центров скоростей, и, соответственно, постоянно равны нулю их мощности.

Работу будут совершать моменты сопротивления каче­нию:

 

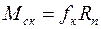и ,

а именно:

,

где

.

 

Здесь φ — угол поворота барабанов, для которого, ин­тегрируя уравнение кинематической связи ω = v/r с уче­том нулевых начальных условий для перемещений s и φ, легко получаем φ = s/r. Тогда

 

 

Внутренние силы. Запишем, учитывая, что кузов не вращается, суммарную работу внутренних сил (моментов) М и М’:

 

.

 

Тогда сумма работ всех сил запишется в виде

 

.

 

Множитель, стоящий в этой формуле перед перемеще­нием s, — это приведенная сила системы

Итак

Дж.

 

Собирая правую и левую части теоремы, получаем

 

или Т – 125,6 = 760, откуда

 

и

 

Ответ: v = 0,53 м/с.