Булевы тождества. Нормальная форма Кантора

 

Булевы тождества(названы по имени Дж.Буля – основателя математической логики) - система теоретико-множественных тождеств (законов), которым подчиняются введенные выше операции над множествами.

Система полна в том смысле, что любое соотношение между множествами является следствием булевых тождеств. В систему булевых тождеств входят следующие группы соотношений (равенств, правил выполнения преобразований множеств):

1) коммутативность (переместительность) объединения и пересечения

А+В = В+А, А∙В = В∙А;

2) ассоциативность (сочетательность) объединения и пересечения

А+ (В+С) = (А+В) + С, А (В∙С) = (А∙В) С;

3) дистрибутивность (распределительность) пересечения относительно объединения и объединения относительно пересечения

А (В+С) = А∙В+А∙С, А + (В∙С) = (А+В) (А+С);

4) идемпотентность объединения и пересечения

А + А = А, А∙А = А;

5) действия с универсальным U и пустым Æ множествами

А + Æ = А, A + U = U, A∙Æ = Æ, A∙U = A, A + Ā = U, A∙Ā = Æ, Ū = Æ;

 

6) двойственность (законы де-Моргана)

, ;

7) правило двойного дополнения (отрицания) – закон инволюции

.

 

Нормальная форма Кантора (НФК)множества. Пусть имеются n произвольных множеств 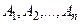. Рассмотрим различные произведения (пересечения), составленные из исходных множеств и их дополнений . На основании булевых тождеств (входящих в четвертую и пятую группы) можно считать, что каждая буква (с черточкой и без черточки) входит в произведение не более одного раза, так как в противном случае произведение либо упрощается, либо равно Æ.

Потребуем, чтобы каждая буква входила в произведение только один раз. Такие произведения называются конституентами (составляющими). Пользуясь законом коммутативности, будем располагать буквы в порядке возрастания их номеров. Тогдаконституента есть не что иное, как произведение, в котором, во-первых, ровно n сомножителей и, во-вторых, каждый i-й сомножитель – это (i = 1,2,…,n).

Выражение, задающее некоторое множество М в виде объединения различных элементарных пересечений (конституент), называется нормальной формой Кантора множества М.

Замечание. Ясно, что НФК конкретного множества не обязательно содержит все возможные конституенты. Так, например, если множество М получено в результате операций над тремя множествами (т.е. при n = 3 ), то его НФК будет содержать не более 8 возможных конституент:

 

.

 

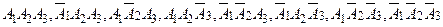Так как равные множества имеют одинаковую НФК (один и тот же состав конституент), то представление множеств в виде НФК может быть, в частности, использовано для их сравнения (проверки на совпадение).

Алгоритм (правила) приведения множества к НФК (см. пример 1.5). Процесс приведения множества к сумме элементарных пересечений (конституент) в общем случае распадается на следующие этапы:

1) с помощью законов де-Моргана и двойного дополнения добиваемся того, чтобы черточки (причем не более одной) стояли только над буквами;

2) пользуясь законом дистрибутивности пересечения, раскрываем скобки и приводим к выражению вида сумма произведений;

3) одинаковые множители в произведениях заменяем одним (свойство идемпотентности пересечения);

4) произведения, содержащие некоторую букву и ту же букву с черточкой (множество и его дополнение), удаляем (в силу тождеств пятой группы);

5) если некоторое произведение содержит менее n букв, то для

добавления недостающих букв используется одно из следствий булевых тождеств - закон склеивания, в соответствии с которым

 

" А, В: В = В (А+ Ā) = ВА + ВĀ;

 

6) если в результате преобразований полученная сумма

произведений содержит одинаковые слагаемые, то из них оставляем только одно (свойство идемпотентности объединения).