Задание 7. Решение систем линейных уравнений методом Гаусса – 2 ч.

Цель: формирование умения решать системы линейных уравнений методом Гаусса.

Задание для самостоятельной внеаудиторной работы:

& 7.1.Изучите теоретические основы решения системы линейных уравнений методом Гаусса, критерий Кронекера-Капелли. Закончите высказывания:

а) для решения системы линейных методом Гаусса необходимо:

· составить … матрицу из коэффициентов при неизвестных и расширенную из …

· привести расширенную матрицу к ступенчатому виду с помощью …

· определить …

· в случае существования решений восстановить систему линейных уравнений, равносильную исходной, начиная с последнего уравнения, и …

б) если ранг основной равен рангу расширенной матрицы и совпадает с числом переменных, то …

если ранг основной равен рангу расширенной матрицы и не совпадает с числом переменных, то …

если ранг основной не равен рангу расширенной матрицы, то …

?7.2. Решите систему линейных уравнений методом Гаусса:

а) б) в)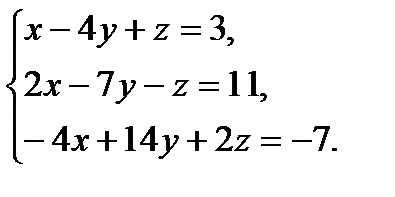

?7.3. Решите систему линейных уравнений по правилу Крамера и методом Гаусса:

7.4. Фирма для перевозки грузов может заказывать машины трех видов. Если она закажет по одной машине каждого вида, то перевезёт 12 тонн груза. Если закажет по две машины первого и второго вида и одну машину третьего вида, то перевезёт 19 тонн груза. Если же фирма закажет по две машины первого и третьего вида и одну машину второго вида, то перевезёт 20 тонн груза. Какова грузоподъемность каждого вида машин?

Методические указания по выполнению работы:

Алгоритм метода Гаусса решения систем линейных уравнений:

1. Составьте расширенную матрицу системы – матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов.

2. С помощью элементарных преобразований приведите полученную матрицу к ступенчатому виду.

3. Определите число решений системы линейных уравнений, используя теорему Кронекера-Капелли

система линейных уравнений с n неизвестными имеет решения тогда и только тогда, когда ранг основной матрицы (матрицы, составленной только из коэффициентов при неизвестных) равен рангу расширенной матрицы r, причем:

1. если r = n(ранг матрицы равен числу неизвестных), то система имеет единственное решение;

2. если r < n (ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.

4. В случае существования решений восстановите систему линейных уравнений, равносильную исходной, начиная с последнего уравнения, и найдите значения неизвестных.

Метод Гаусса является более универсальным, чем правило Крамера, так как позволяет находить решения в следующих случаях:

1. число уравнений не равно числу неизвестных.

2. если в правиле Крамера ∆ = ∆х= ∆у = ∆z= 0.

Все возможные случаи решения системы линейных уравнений (одно решение, нет решений, множество решений) разобраны в примерах 1 – 3.

Пример 1.Решите систему уравнений методом Гаусса:

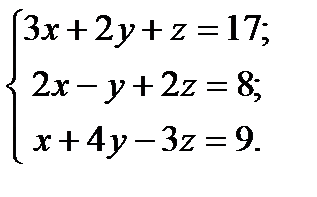
Решение. 1. Выпишем расширенную матрицу системы: .

2. Приведем её к ступенчатому виду. Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных коэффициентов при последующих вычислениях: .

Первую строку полученной матрицы умножаем последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом А будет иметь вид:

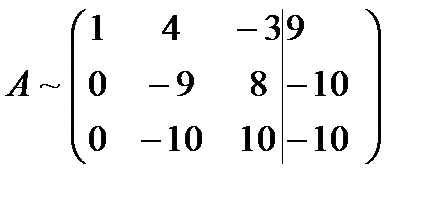
Для упрощения вычислений умножим третью строку на (-0,1) и поменяем ее местами со второй строкой. Тогда получим:

Далее, умножая вторую строку матрицы на 9 и складывая с третьей, окончательно получим:

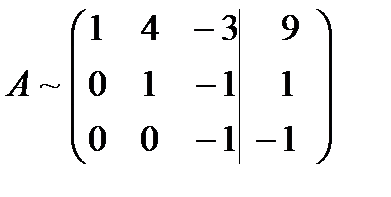- матрица ступенчатого вида.

3. Определим число решений системы уравнений. Ранг основной матрицы равен 3, расширенной тоже 3, следовательно в силу критерия Кронекера-Капелли система имеет единственное решение. 4. Найдём его. Восстановим из полученной матрицы А систему уравнений, равносильную данной, начиная с последнего уравнения:

Из последнего уравнения находим: z = 1.

Подставим z = 1 во второе уравнение системы: y – 1 = 1; y = 2.

После подстановки z = 1 и y = 2 в первое уравнение получим: x + 4·2 - 3·1 = 9;

x = 9 – 8 + 3; x = 4. Итак, x = 4, y = 2, z = 1.

Проверка:

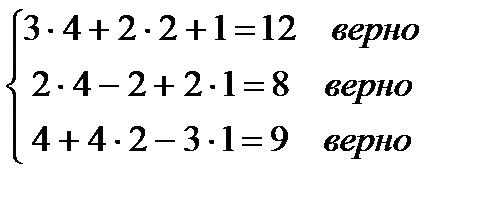
Следовательно, решение системы найдено верно.

Ответ: x = 4, y = 2, z = 1.

Пример 2.Найдите все решения системы линейных уравнений:

Решение. 1. Составим расширенную матрицу системы:

2. Приведем ее к ступенчатому виду. Домножим первую строку на (-2) и сложим ее со второй строкой: ~ .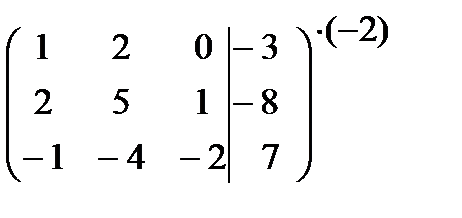

Сложим первую и третью строки: .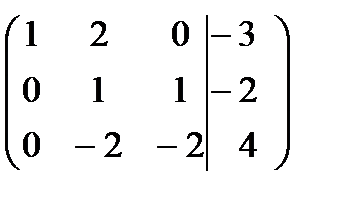

Домножим вторую строку на 2 и сложим ее с третьей строкой: .

Вычеркнем нулевую строку: - матрица ступенчатого вида.

3. Определим число решений системы уравнений. Видим, что ранг основной матрицы равен рангу расширенной матрицы и равен двум. Следовательно, в силу критерия Кронекера-Капелли, система имеет решения. Так как ранг матрицы (два) меньше числа неизвестных (три), то система имеет бесчисленное множество решений.

4. Найдем эти решения. Восстановим систему уравнений, равносильную исходной:

Пусть z – свободная переменная, которая может принимать любые числовые значения. Выразим из первого уравнения y: y = -z – 2.

Подставим данное выражение y = -z – 2во второе уравнение:

x = -2у – 3; x = -2·(-z - 2) – 3; x = 2z + 4 – 3; x = 2z + 1.

Такое решение будем называть общим решением системы. Запишем общее решение системы в виде тройки чисел: (2z + 1; -z – 2; z).

Ответ: (2z + 1; -z – 2; z).

Пример 3.Докажите, что система линейных уравнений не имеет решений:

Решение. 1. Составим расширенную матрицу системы: .

2. Приведем ее к ступенчатому виду. Домножим первую строку на (-3) и сложим ее со второй строкой: ~ .

Домножим первую строку на 2 и сложим ее с третьей строкой:

~ .

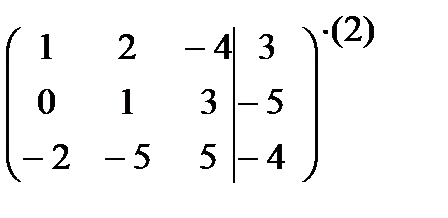Сложим вторую и третью строки: .

3. Определим число решений системы уравнений. Видим, что ранг основной матрицы (2) не равен рангу расширенной матрицы (3). Следовательно, в силу критерия Кронекера-Капелли система не имеет решений.

Ответ: решений нет.

Список литературы:

1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 2, §2.4, стр. 40 – 51.

2. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 1, §5, 6, стр. 85 – 91.