Алгоритм нахождения обратной матрицы.
1. Вычислите определитель матрицы А, проверьте условие: |A|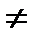 
0.
2. Найдите алгебраические дополнения элементов матрицы А и составьте матрицу алгебраических дополнений А*:
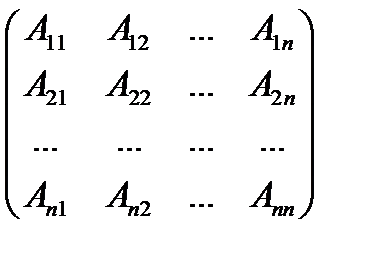
А* =
3. Составьте матрицу (А*)т, транспонируя матрицу А*.
4. Найдите обратную матрицу по формуле:
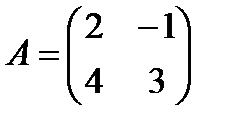
Пример 1. Найдите матрицу, обратную матрице
Решение: 1. Находим определитель матрицы А:
|A| =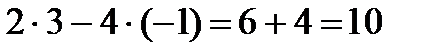 
2.Найдем алгебраические дополнения каждого элемента матрицы А:
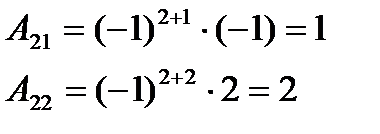
Составляем матрицу из алгебраических дополнений А*: А*=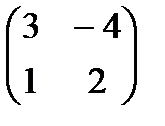 
- Транспонируем матрицу А*:
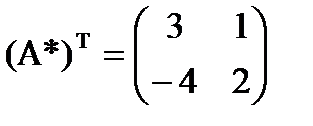
- Составляем обратную матрицу по формуле:
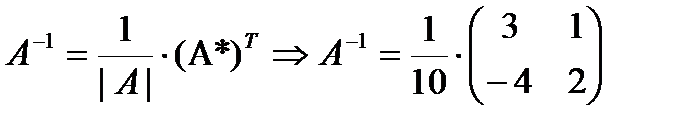
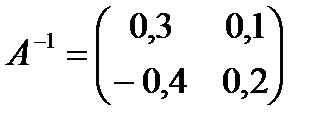
Проверим, действительно ли матрица А-1 является обратной к матрице А. Должно выполняться равенство: 
, где Е – единичная матрица.
.
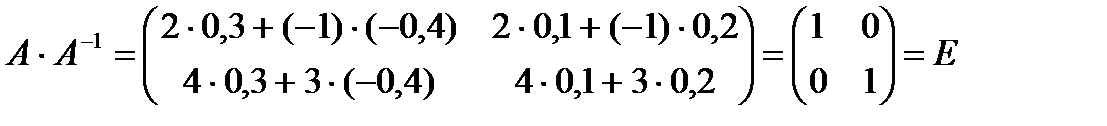Получили, что , следовательно, матрица А-1 является обратной к матрице А.
Ответ: .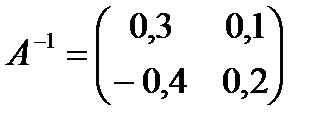
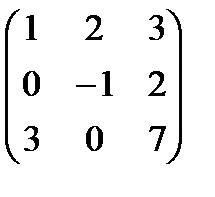
Пример 2. Найдите матрицу, обратную матрице А = .
Решение: 1. Находим определитель матрицы А.
|A|=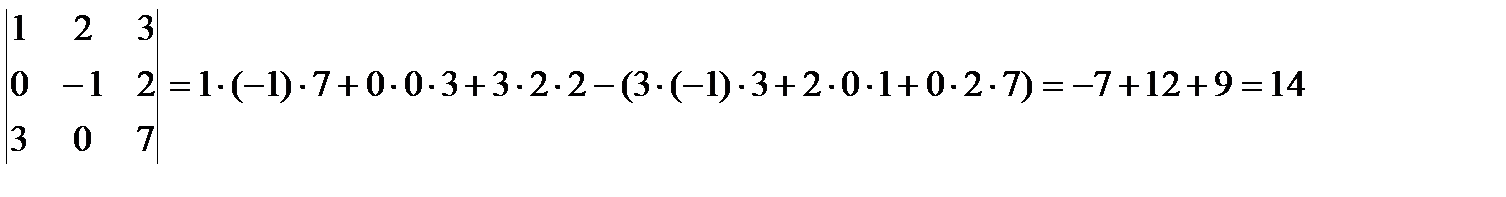 
;
14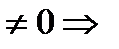 
матрица 
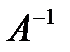существует.
2. Найдем алгебраические дополнения каждого элемента матрицы А:
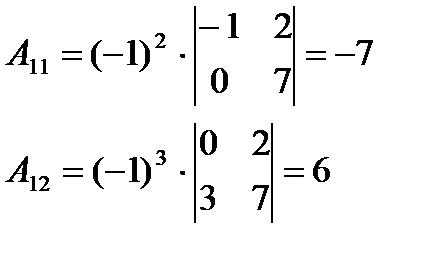
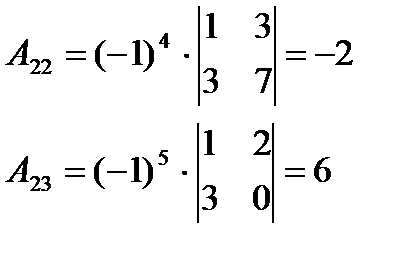
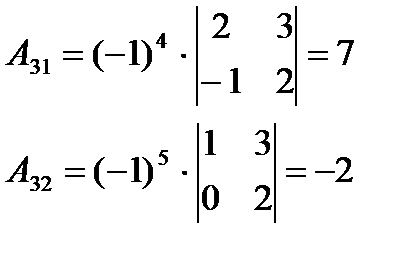
Составляем матрицу из алгебраических дополнений А*: А*=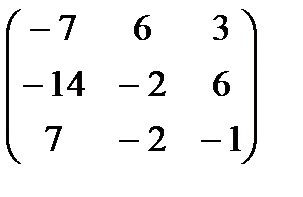 
.
3. Транспонируем матрицу А*: (А*)Т=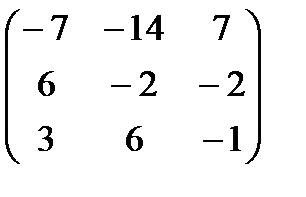 
.
4.Составляем обратную матрицу по формуле:
.
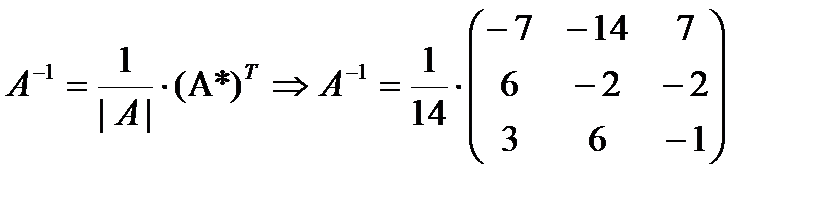Ответ: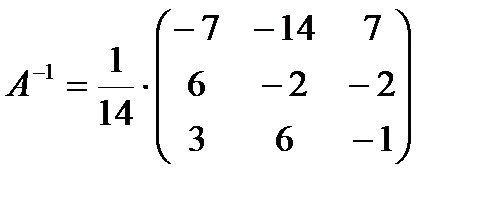 
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 2, §2.3, стр. 33 – 36.
2. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 1, §3, стр. 78 – 81.