Токоведущей цепи

4.3.1. ЭДУ между параллельными проводниками. Сила взаимодействия между двумя проводниками, расположенными параллельно и обтекаемыми токами i₁ и i₂, определяется следующим образом:

а) если один проводник имеет бесконечную длину, а второй имеет длину l и расположен симметрично относительно первого, то

, (84)

б) если оба проводника имеют конечную длину, т.е. l₁=l₂=l, то

. (85)

Приведенные формулы справедливы для провод-

ников круглого и трубчатого сечений, для которых можно считать, что ток протекает по их геометрической оси. Для проводников прямоугольного сечения (шин) вводится поправочный коэффициент – коэффициент формы К_ф, зависящий от размеров проводников и расстояний между ними

. (86)

Рис. 33. К расчету ЭДУ между

параллельными проводниками

 

4.3.2. ЭДУ между взаимно перпендикулярными проводниками. Такое расположение проводников встречается в распределительных шкафах, в присоединительных токоподводящих шинах и др.

а) При h = , (87)

б) при h конечном . (88)

Момент сил относительно точки О (рис. 34).

, . (89)

4.3.3. Эду в кольцевом витке и между кольцевыми витками. В кольцевом витке с током i возникают радиальные силы f_r, стремящиеся увеличить его периметр,

т.е. разорвать виток:

а) для витка круглого сечения

при R >> r

, (90)

где R – радиус витка; r – радиус провода;

Рис. 34. К расчету ЭДУ между

перпендикулярными проводниками б) для витка прямоугольного сечения

. (91)

Эти формулы применимы не только к одному витку, но и к обмоткам с любым числом витков, занимающим данное сечение. В катушках аппаратов, кроме сил, действующих внутри каждого витка, будут существовать ЭДУ между витками.

При одинаковом направлении тока в витках, между витками возникает сила притяжения F, которую можно представить как результирующую двух сил F_x и F_y.

F_x – сила, стремящаяся притянуть витки друг к другу; F_y – сила, стремящаяся один виток, а именно виток с меньшим диаметром (при одинаково направленных токах) растянуть, а другой виток, большего диаметра – сжать.

Рис. 35. К расчету ЭДУ Таким образом, в одном из витков сила

в кольцевом витке F_x будет складываться с силой F_r, а в дру-

гом вычитаться из нее.

Силы F_x и F_y зависят от расстояния между витками.

, (92)

 

, (96)

Рис. 36. Зависимость F_x и F_y от h где .

4.3.4. ЭДУ в проводниках переменного сечения. В проводнике силы взаимодействия отдельных линий тока с собственным магнитным полем проводника, направлены перпендикулярно линиям тока. При неизменном сечении проводника все нити тока параллельны и силы не имеют осевой составляющей (в цилиндрическом проводнике они направлены по радиусу).

При изменении сечения проводника

Рис. 37. ЭДУ в проводнике линии тока искривляются и, кроме попе- переменного сечения речной силы F_r, появляется продольная составляющая F_l, стремящаяся разорвать проводник в узком сечении (рис. 37). Эта сила всегда направлена в сторону большего сечения проводника и равна:

. (94)

4.3.5. ЭДУ между проводником с током и ферромагнитной массой. Вблизи ферромагнитной массы магнитное поле вокруг проводника с током искажается, магнитные силовые линии стремятся замкнуться на массе. В результате этого возникают силы, стремящиеся притянуть проводник к этой массе. Значение силы притяжения может быть определено из следующих

Рис. 38. ЭДУ между соображений. Заменим действие ферромагнит-

проводником и Fe массой ной массы вторым проводником с током того же

направления, расположенным на таком же расстоянии от границы раздела сред. Картина поля при этом не нарушится, так как одновременно с удвоением длины магнитной силовой линии удвоилась и магнитодвижущая сила, то есть такая замена вполне правомерна (рис. 38).

Сила взаимодействия между двумя параллельными проводниками подсчитывается по (85) и (86). Только в данном случае вместо размера а надо брать 2а, т. е.

. (95)

Если проводник с током находится в щели, образованнойстенками из ферромагнитной массы (рис. 39), то электродинамические

силы будут отталкивать проводник от гра-

ницы раздела воздуха и ферромагнитной массы, то есть проводник будет затягиваться в щель. Сила, действующая на проводник, в этом случае определяется выражением:

. (96)

Здесь l – длина щели, – ширина щели в

Рис. 39. ЭДУ на проводник месте расположения проводника.

в щели железной массы В щели постоянного сечения сила, затяги-

вающая проводник вглубь, будет неизменной, а в щели переменного сечения – переменной, возрастающей по мере сужения щели. Этот случай используется для гашения электрической дуги в дугогасительных решетках.

4.3.6. ЭДУ при переменном однофазном токе. Рассмотрим силы, действующие между параллельными проводниками. Согласно выражению (86) для этого случая, ЭДУ будет равно:

.

Для конкретной системы можно положить, что при i₁=i₂ и

, то .

На переменном токе , тогда сила будет равна:

. (97)

Отсюда следует, что ЭДУ на переменном

Рис. 40. ЭДУ на переменном токе токе состоит из двух составляющих –

постоянной и переменной .

Причем, переменная составляющая ЭДУ пульсирует с двойной частотой сети по косинусоидальному закону и дважды за период изменяется по величине от максимального значения до нуля (рис. 40). В расчетах учитывается максимальное значение силы

, где .

Отсюда видно, что при переменном однофазном токе максимальное значение ЭДУ при одном и том же токе в два раза больше, чем на постоянном. Однако, в отличие от постоянного тока, при котором максимальное значение тока короткого замыкания равно его установившемуся значению I_уст при R = const, при переменном токе в зависимости от момента к.з. первая амплитуда ударного тока i_уд.max может существенно превосходить амплитудное значение установившегося тока к.з. (рис. 41)

. (98)

Максимальное усилие, на которое следует рассчитывать устройство, будет равно:

, (99)

то есть, при равном значении установившегося тока к.з. при переменном токе ЭДУ может быть почти в 6,5 раза больше, чем при постоянном токе.

4.3.7. ЭДУ в трехфазной сети. При трехфазной сети токи в фазах будут сдвинуты относительно друг друга на 120 электрических градусов

, (100)

, (101)

. (102)

Случай, когда проводники расположены в одной плоскости на равном расстоянии друг от друга (рис. 42). Проводник 1 будет взаимодействовать с проводниками 2 и 3. Пусть ЭДУ между проводниками 1 и 2 равно F₁₂, а между проводниками 1 и 3 – F₁₃. Токи в фазах

раны. Тогда полная сила, действующая на проводник 1, будет равна:

.

(103)

В отличие от однофазного тока при

Рис. 41. ЭДУ в однофазной сети 3-х фазном токе сила меняется не только во времени, но и по знаку. При положительных значениях и получим силу, притягивающую проводник 1 к двум другим проводникам.

При отрицательных значениях sin и cos получим силу, отталкивающую проводник 1 от двух других. Так как расстояние между про-

водниками одинаково, то F₁₃ = 0.5F₁₂ и тогда в установившемся режиме максимальная притягивающая сила

. (104)

Максимальная отталкивающая сила

. (105)

ЭДУ, действующие на проводник 3, будут аналогичными, а на проводник 2

. (106)

С учетом переходной составляющей, возникающей в момент

короткого замыкания, максималь-

Рис. 42. ЭДУ в трехфазной системе ные ЭДУ будут большими, чем по

вышеприведенным формулам.

В момент возникновения к.з.

F_1от.max= 6.48F₁₂I² при ; F_1пр = 0;

F_1пр.max= 0.468F₁₂I при ; F_1от = 0.75F₁₂ .

Вопросы для самоконтроля

4.4.1. Определите направление действия ЭДУ на проводник с током, находящийся между полюсами 1 и 2 электромагнита. Направление токов в проводнике и в катушке электромагнита показано на рис. 43.

 

Рис. 43. К определению направления действия ЭДУ

4.4.2. Чем отличаются выражения для ЭДУ между параллельными проводниками бесконечной и конечной длины?

4.4.3. Как влияет форма сечения проводников на величину электродинамической силы?

4.4.4. Как рассчитываются ЭДУ в круговом витке и между витками?

4.4.6. Покажите направление магнитных силовых линий поля между полюсами (рис. 44). Сделайте обозначение полярности полюсов электромагнитов. Определите направление действия ЭДУ на проводник с током, расположенный между полюсами.

 

Рис. 44. К определению полярности полюсов и направления действия ЭДУ

 

4.4.7. Чем обусловлена сила отталкивания контактов, и к каким вредным последствиям она может привести?

4.4.8. Объясните причину возникновения электродинамической силы между проводником с током и ферромагнитным телом, и приведите пример ее использования в электрических аппаратах.

4.4.9.

Рис. 3

Как рассчитываются ЭДУ внутри контура с током и между токоведущими контурами с помощью энергетического метода.

4.4.10. Как отреагирует деталь 3 (рис. 45), свободно лежащая на полюсах электромагнита 1, если в катушку 2 подать импульс тока путем разряда конденсатора С через замыкающий ключ К в случае, если деталь 3 выполнена: из стали, из меди, из пластмассы? Обоснуйте ответы.

Рис. 45. К определению направления действия ЭДУ на деталь

4.4.11.Объясните суть первого метода расчета электродинамических сил (на основе закона Ампера).

4.4.12. В каком случае ЭДУ между проводниками прямоугольного сечения, обтекаемыми токами, будут больше: при взаимном расположении по рис. 46,а или по рис. 46,б? Обоснуйте ответ.

Рис. 46. К определению влияния 4.4.13. С позиции теории ЭДУ объясните

взаимного расположения принцип действия устройства, состоящего

проводников на ЭДУ из С-образного электромагнита перемен-

ного тока, между полюсами которого расположен алюминиевый диск (например: счетчик электроэнергии).

4.4.14. Что понимается под электродинамической стойкостью электрических аппаратов.

4.4.15. Как направлены ЭДУ и моменты в системах взаимно перпендикулярных проводников?

4.4.16. Приведите примеры устройств, принцип действия которых основан на взаимодействии проводника с током и ферромагнитным телом.

4.5. Примеры расчета [6]

 

4.5.1. Определить величину ЭДУ, возникающего между двумя расположенными параллельно друг другу шинами прямоугольного сечения h x b = 100 x 10 мм на длине l = 2 м. Расстояние между осями шин а = 20 мм, по ним протекает ток короткого замыкания I_кз = 54 кА. Шины находятся в воздухе вдали от ферромагнитных частей и ток распределен равномерно по их сечению. Шины расположены широкими сторонами друг к другу.

Решение. Величина ЭДУ определяется по формуле

.

Для данного расположения проводников величина соотношения

; .

Коэффициент формы из [6] равен k_ф = 0,44.

Тогда Н.

4.5.2. Определить ЭДУ, действующее на проводник 1, со стороны проводника 2 (рис. 47), если по проводникам протекает постоянный ток I = 12 кА, а длины участков l₁ = 1 м, l₂ = 2 м. Проводники круглые диаметром d = 10 мм и находятся в воздухе на достаточном удалении от ферромагнитных частей.

Рис. 47. К расчету ЭДУ Ршение.Выделим элементы проводников dl₁ dl₂ и определим элементарную силу, действующую со стороны элемента dl₂ на элемент dl₁. Так как проводники находятся в одной плоскости, то со стороны проводника 2 на проводник 1 действует элементарная сила

, (107)

или для 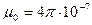Гн/м,

.

Суммарная сила, действующая на проводник 1,

. (108)

Здесь

; ; ; ; .

После интегрирования и, учитывая, что , получаем

Н.

 

4.5.3. Определить ЭДУ, действующее между параллельно расположенными шинами, если I₁ = 10 кА, I₂ =15 кА, l₁ = 1м, l₂ =1,5 м, а = 0,5 м.

Решение.ЭДУ определим по формуле

.

Коэффициент контура электродинамических усилий [6]

, (109)

для воздуха 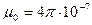Гн/м.

Тогда, Н.

 

4.5.4. Определить усилие, разрывающее проводник с током I =100 кА в месте, где проводник изменяет свое поперечное сечение от D = 50 мм до d = 20 мм.

Решение.Для нахождения усилия, разрывающего проводник, воспользуемся формулой

Н.

 

4.5.5. На каком минимальном расстоянии можно поставить опорные изоляторы в распределительном устройстве, если в нем применены прямоугольные медные шины сечением 100 х 10 мм по одной шине на фазу. Шины закреплены жестко на опорах, поставлены на ребро и по ним протекает ток трехфазного короткого замыкания, установившееся значение которого I_уст = 507 кА. Расстояние между фазами равно 0,3 м.

Решение.Определим значение ЭДУ, действующего на 1 м длины шин, при этом расчетное значение тока определим по формуле

кА.

Здесь k_уд= 1,8.

Сила, действующая на 1 м длины

Н/м.

Для многопролетной балки [6]

, (110)

где – момент сопротивления поперечного сечения шины; Н/м – допустимое напряжение на изгиб для меди.

Подставив числовые значения, получим

,

откуда l_1мин = 0,65 м.

Поскольку по шинам протекает переменный ток, необходимо найти минимальное расстояние между изоляторами в случае отсутствия механического резонанса. При этом, собственная частота шин должна быть меньше частоты механических колебаний, т. е. двойной частоты тока: , (111)

где k = 112 для жесткого закрепления шин; E = 11,8∙10⁶ Н/см² – модуль упругости для меди; см⁴ – момент инерции сечения шины; γ = 85,2 Н/см³ – удельный вес меди; S –поперечное сечение шины.

После решения равенства (114) относительно l_2мин получаем требуемое расстояние между изоляторами

l_2мин = 0,596 м.

Выбираем наименьшее из двух полученных значений, т. е.

l_мин = 0,6 м.