Зависимость константы скорости реакции от температуры

Скорость большинства химических реакций возрастает при повышении температуры. Так как концентрация реагирующих веществ, практически не зависит от температуры, то в соответствии с кинетическим уравнением реакции основное влияние температуры на скорость реакции осуществляется через изменение константы скорости реакции. При увеличении температуры возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение.

Зависимость скорости реакции от температуры можно характеризовать величиной температурного коэффициента .

Экспериментальные данные по влиянию температуры на скорость многих химических реакций при обычных температурах (273–373 К), в небольшом интервале температур показали, что повышение температуры на 10 градусов увеличивает скорость реакции в 2-4 раза (правило Вант-Гоффа).

По Вант-Гоффу- температурный коэффициент константы скорости (коэффициент Вант-Гоффа) – это возрастание скорости реакции при увеличении температуры на 10 градусов.

 

(4.63)

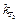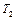где и — константы скорости при температурах и ; — температурный коэффициент скорости реакции.

При повышении температуры на n десятков градусов отношение констант скоростей будет равно

 

, (4.64)

где n может быть как целым, так и дробным числом.

Правило Вант-Гоффа это приближенное правило. Оно применимо в узком интервале температур, так как температурный коэффициент изменяется с температурой.

Более точная зависимость константы скорости реакции от температуры выражается полуэмпирическим уравнением Аррениуса

(4.65)

где А - предэкспоненциальный множитель который не зависит от температуры, а определяется только видом реакции; Е – энергия активации химической реакции. Энергию активации можно представить как некоторую пороговую энергию, характеризующую высоту энергетического барьера на пути реакции. Энергия активации также не зависит от температуры.

Эта зависимость установлена в конце XIX в. голландским ученым Аррениусом для элементарных химических реакций.

Энергия активации прямой (Е₁ ) и обратной (Е₂ ) реакции связана с тепловым эффектом реакции DН соотношением (см. рис 1):

Е₁ – Е₂ = DН.

Если реакция эндотермическая и DН> 0, то Е₁ > Е₂ и энергия активации прямой реакции больше обратной. Если реакция экзотермическая, то Е₁ < Е₂.

Уравнение Аррениуса (101) в дифференциальной форме можно записать:

 

. (4.66)

Из уравнения следует, что чем больше энергия активации Е, тем быстрее растет скорость реакции с температурой.

Разделив переменные k и T и, считая E постоянной величиной, после интегрирования уравнения (4.66) получим:

Рис. 5. График lnk –1/T.

, (4.67)

где А – предэкспоненциальный множитель, имеющий размерность константы скорости. Если это уравнение справедливо, то на графике в координатах опытные точки располагаются на прямой линии под углом a к оси абсцисс и угловой коэффициент ( ) равен , что позволяет рассчитать энергию активации химической реакции по зависимости константы скорости от температуры по уравнению .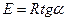

Энергию активации химической реакции можно вычислить по значениям констант скоростей при двух различных температурах по уравнению

. (4.68)

Теоретический вывод уравнения Аррениуса сделан для элементарных реакций. Но опыт показывает, что подавляющее большинство сложных реакций также подчиняются этому уравнению. Однако для сложных реакций энергия активации и предэкспоненциальный множитель в уравнении Аррениуса не имеют определенного физического смысла.

Уравнение Аррениуса (4.67) позволяет дать удовлетворительное описание большого круга реакций в узком температурном интервале.

Для описания зависимости скорости реакции от температуры применяют также модифицированное уравнение Аррениуса

,(4.69)

в которое входят уже три параметра:А, Е и n.

Уравнение (4.69) широко используется для реакций, протекающих в растворах. Для некоторых реакций зависимость константы скорости реакции от температуры отличается от приведенных выше зависимостей. Так, например, в реакциях третьего порядка константа скорости убывает с увеличением температуры. В цепных экзотермических реакциях константа скорости реакции резко возрастает при температуре выше некоторого предела (тепловой взрыв).

4.5.1. Примеры решения задач

Пример 1. Константа скорости некоторой реакции с увеличением температуры изменялась следующим образом: t₁ = 20°С;

k₁ = 2,76 10^-4 мин.^-1; t₂ = 50 ⁰С; k₂= 137,4 10^-4 мин.^-1 Определить температурный коэффициент константы скорости химической реакции.

Решение. Правило Вант –Гоффа позволяет рассчитать температурный коэффициент константы скорости по соотношению

gⁿ = =2 ¸ 4, где n = = =3;

g³ = =49,78 g = 3,68

Пример 2.С помощью правила Вант-Гоффа вычислить, при какой температуре реакция закончится за 15 мин., если при температуре 20 ⁰С потребовалось 120 мин. Температурный коэффициент скорости реакции равен 3.

Решение. Очевидно, чем меньше время протекания реакции (t), тем больше константа скорости реакции:

= = = ;

3ⁿ = 8, nln3 = ln8, n= = .

Температура, при которой реакция закончится за 15 минут, равна:

20 + 1,9×10 = 39 ⁰С.

Пример 3.Константа скорости реакции омыления уксусно-этилового эфира раствором щелочи при температуре 282,4 К равна2,37л²/моль²мин_., а при температуре 287,40 К равна 3,2л²/моль²мин. Найти, при какой температуре константа скорости данной реакции равна 4?