Краткая теория
ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА
Краткая теория
В качестве меры механического воздействия в механике вводится векторная величина, называемая силой 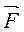 . Сила гравитационного притяжения,действующая между двумя материальными точками. Согласно закону всемирного тяготения: все тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс тел и обратно пропорциональной квадрату расстояния между ними.
. Сила гравитационного притяжения,действующая между двумя материальными точками. Согласно закону всемирного тяготения: все тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс тел и обратно пропорциональной квадрату расстояния между ними.
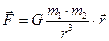
| (3.1) |
где G = 6,67 × 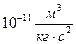 - гравитационная постоянная,
- гравитационная постоянная, 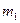 и
и 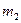 - массы первого и второго тела, r - расстояние между телами.
- массы первого и второго тела, r - расстояние между телами.
Если тела имеют большие размеры (Земля, другие планеты), расстояние R нужно брать до их центра.
Сила тяжести — это сила всемирного тяготения между Землей и телами, находящимися около ее поверхности. Экспериментальным путем установлено, что 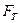 = mg. Следовательно,
= mg. Следовательно, 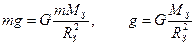 - ускорение свободного падения на поверхности Земли.
- ускорение свободного падения на поверхности Земли.
Если тело находится на достаточной высоте Н над Землей, ускорение свободного падения уменьшается, и может быть найдено по формуле:
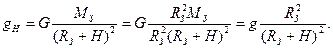
Вес тела - это сила, с которой тела действуют на опору или подвес:
1) Р = 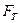 = mg — тело находится в покое или движется равномерно вместе с опорой;
= mg — тело находится в покое или движется равномерно вместе с опорой;
2) Р = m(g-a) — тело движется вертикально вниз вместе с опорой с ускорением а.
Частный случай — тело свободно падает вместе с опорой. В этом случае a = g. Следовательно, P = 0. В таких случаях явление исчезновения веса называют невесомостью.
3) Р = m(g+a) — тело движется вертикально вверх вместе с опорой с ускорением а. Такое состояние называют перегрузкой. Значительные перегрузки (иногда в 5 - 6 раз больше нормального веса) испытывают космонавты при старте. Они же испытывают невесомость при свободном движении корабля по орбите вокруг Земли.
Сила трения. Сила трения скольжения возникает во время движения одного тела по поверхности другого. Эта сила всегда противодействует движению. Природа ее объясняется существованием взаимодействия между молекулами и атомами соприкасающихся тел.
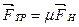
| (3.2) |
где 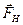 — сила нормального давления на опору, m — коэффициент трения, который зависит от вещества соприкасающихся тел, а также от качества обработки соприкасающихся поверхностей. При равномерном движении по горизонтали, когда перпендикулярно движению действует только сила тяжести:
— сила нормального давления на опору, m — коэффициент трения, который зависит от вещества соприкасающихся тел, а также от качества обработки соприкасающихся поверхностей. При равномерном движении по горизонтали, когда перпендикулярно движению действует только сила тяжести: 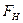 = mg, следовательно,
= mg, следовательно, 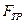 = mmg .
= mmg .
Сила упругости — сила, возникающая при деформации тела и направленная в сторону, противоположную перемещению частиц или частей тела при деформации. Природа сил упругости объясняется силами отталкивания и притяжения между атомами и молекулами вещества.
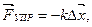
| (3.3) |
где Dx — изменение размера тела, k — коэффициент упругости или жесткость тела, который зависит от материала тела и от его размеров.
Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости. Эта сила зависит от скорости тела относительно среды, причем направлена противоположно вектору 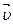 :
:
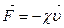
| (3.4) |
где c - положительный коэффициент характерный для данного тела и данной среды. Этот коэффициент зависит от скорости υ, однако при малых скоростях во многих случаях его можно практически считать постоянным.
Первый закон Ньютона: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.
Первый закон Ньютона называютзаконом инерции, а свойство тел сохранять состояние покоя или равномерного прямолинейного движения при отсутствии воздействия на них других тел называютинертностью.
Экспериментпоказывает, что всякое тело «оказывает сопротивление» при любых попытках изменить его скорость – как по модулю, так и по направлению. У различных тел оно проявляется в разной степени. Мерой инертности служит величина, называемая массой. Тело с большей массой является более инертным, и наоборот. В рамках ньютоновской механики масса обладает следующими двумя важнейшими свойствами:
1) масса – величина аддитивная, то есть масса составного тела равна сумме масс его частей m = S 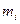
2) масса тела как такового – величина постоянная, не изменяющаяся при его движении.
Первый закон Ньютона так же, как и остальные законы механики, выполняется не во всякой системе отсчета. Системы отсчета, по отношению к которым выполняется первый закон Ньютона, называютсяинерциальными системами отсчета. Как показывает эксперимент, этому условию с весьма большой степенью точности удовлетворяет система отсчета, связанная с Солнцем, — начало координат находится в центре Солнца, а оси проведены в направлении определенных звезд. Система отсчета, скрепленная с Землей, строго говоря, неинерциальна. Однако в большинстве практических задач эффекты, обусловленные неинерциальностью земной системы отсчета, пренебрежимо малы. Поэтому в дальнейшем мы будем считать эту систему отсчета инерциальной, а при изложении законов механики будем пользоваться только инерциальными системами отсчета.
Второй закон Ньютона:под действием результирующей силы тело приобретает ускорение
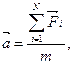
| (3.5) |
где m – масса тела, 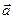 - ускорение,
- ускорение, 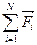 - результирующая сила (геометрическая сумма сил, действующих на тело).
- результирующая сила (геометрическая сумма сил, действующих на тело).
Второй закон Ньютона можно записать в другой форме. Заменим, согласно формуле (1.7): 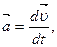
Тогда
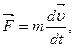
| (3.6) |
Или
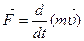
| (3.6¢) |
Вектор m 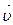 называется импульсом,или количеством движения,тела, а (m
называется импульсом,или количеством движения,тела, а (m 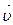 ) представляет собою элементарное изменение вектора импульса. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру его движения (скорость), но и его важнейшее динамическое свойство – массу.
) представляет собою элементарное изменение вектора импульса. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру его движения (скорость), но и его важнейшее динамическое свойство – массу.
С учетом формул (3.5), (3.6) основное уравнение динамики поступательного движениятвердого тела:
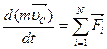
| (3.7) |
где 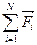 - геометрическая сумма сил, действующих на тело;
- геометрическая сумма сил, действующих на тело; 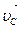 - скорость центра масс тела.
- скорость центра масс тела.
Центром масс,системы материальныхточек называется точка С, радиус-вектор которой равен:
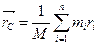
| (3.7¢) |
где 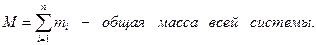
Третий закон Ньютона:каждой силе 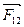 соответствует сила противодействия
соответствует сила противодействия 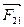 , равная по величине, но противоположно по направлению:
, равная по величине, но противоположно по направлению:
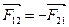
| (3.8) |
Силы 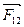 и
и 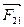 приложены к разным телам. Это силы одной природы. Уравнение (3.6) можно записать в другом виде:
приложены к разным телам. Это силы одной природы. Уравнение (3.6) можно записать в другом виде:
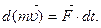
| (3.9) |
где 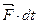 называется элементарным импульсом силы
называется элементарным импульсом силы 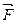 за малый промежуток времени dt.
за малый промежуток времени dt.
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ
3.1. Определение силы.
3.2. Определение результирующей силы.
3.3. Сила гравитационного притяжения.
3.4. Физический смысл гравитационной постоянной.
3.5. Сила тяжести.
3.6. Определение ускорения силы тяжести.
3.7. Вес тела.
3.8. Условия изменения веса тела.
3.9. Сила упругости.
3.10. Сила трения.
3.11. Сила сопротивления.
3.12. Определение инерции.
3.13. Инерциальные системы отсчета.
3.14. Неинерциальные системы отсчета.
3.15. Первый закон Ньютона.
3.16. Определение масс.
3.17. Свойства массы.
3.18. Основной закон динамики поступательного движения для твердого тела.
3.19. Третий закон Ньютона.
3.20. Определение импульса тела.
3.21. Определение центра масс.
3.22. Определение импульса силы.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ:
«ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА»
1. Построить чертеж.
2. Записать следствие из второго закона Ньютона в виде: 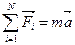 (в векторной форме).
(в векторной форме).
3. Выбрать инерциальную систему отсчета (И.С.О.).
4. Определить проекции сил и ускорения на выбранные оси.
5. Записать дополнительные уравнения, позволяющие определить неизвестные физические величины, входящие во второй закон Ньютона.
6. Решить систему уравнений относительно искомой физической величины.
7. Проверить единицы физических величин измерений справа и слева от знака равенство.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ:
«ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА»
Задача 3.1. Тело массой m скользит по горизонтальной плоскости под действием силы 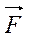 , направленной под углом a к горизонту. Найти ускорение тела, если коэффициент трения равен m.
, направленной под углом a к горизонту. Найти ускорение тела, если коэффициент трения равен m.
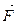   Дано:
a
m
m Дано:
a
m
m
| Решение:
1.
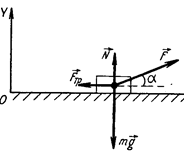 Рисунок к задаче 3.1.
Рисунок к задаче 3.1.
|
| Найти: а - ? |
2. Согласно уравнению (3.5), имеем:
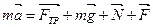
| (1) |
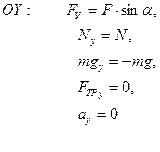 3. И.С.О.: Тело отсчета – Земля; система координат – Декартова; ОХ – горизонтально вправо; ОУ – вертикально вверх; начальная координата – в точке О.
3. И.С.О.: Тело отсчета – Земля; система координат – Декартова; ОХ – горизонтально вправо; ОУ – вертикально вверх; начальная координата – в точке О.
4. 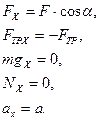 ОХ:
ОХ:
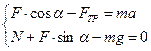
5. Согласно уравнению (3.2): 
6. Решая полученную систему уравнений относительно искомой величины:
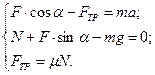
Можно получить: 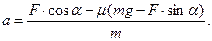
Ответ: 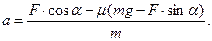
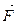 Задача 3.2. По наклонной плоскости, составляющей с горизонтом угол a, движется вверх груз массой m, к которому приложена сила , направленная под углом b к наклонной плоскости. Коэффициент трения скольжения равен m. Найти ускорение тела.
Задача 3.2. По наклонной плоскости, составляющей с горизонтом угол a, движется вверх груз массой m, к которому приложена сила , направленная под углом b к наклонной плоскости. Коэффициент трения скольжения равен m. Найти ускорение тела.
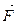   Дано:
a
m
m
b Дано:
a
m
m
b
| Решение:
1. 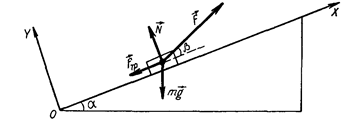 Рисунок к задаче 3.2.
2. Согласно уравнению (3.5), имеем:
Рисунок к задаче 3.2.
2. Согласно уравнению (3.5), имеем:
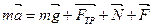 (1)
3. И.С.О.: Тело отсчета – Земля; система координат - Декартова; ОХ – вверх вдоль плоскости; ОУ – вверх перпендикулярно к плоскости. (1)
3. И.С.О.: Тело отсчета – Земля; система координат - Декартова; ОХ – вверх вдоль плоскости; ОУ – вверх перпендикулярно к плоскости.
|
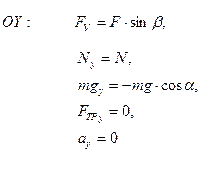 Найти:
а - ? Найти:
а - ?
|
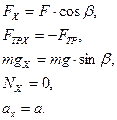 4. ОХ:
4. ОХ:
ОХ: 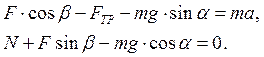
ОУ:
5. Согласно уравнению (3.2): 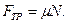
6. Решая полученную систему уравнений относительно искомой величины:
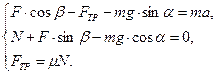
Можно получить: 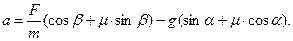
Ответ: 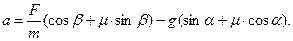
Задача 3.3. Две гири с массами 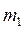 = 2 кг и
= 2 кг и 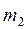 = 1 кг соединены и перекинуты через невесомый блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением в блоке пренебречь.
= 1 кг соединены и перекинуты через невесомый блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением в блоке пренебречь.
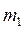 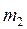   Дано:
= 2 кг
= 1 кг Дано:
= 2 кг
= 1 кг
| Решение:
1.
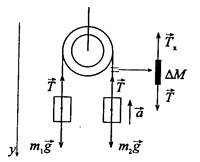 Рисунок к задаче 3.3.
2. Согласно уравнению (3.5), имеем:
Для 1 гири:
Рисунок к задаче 3.3.
2. Согласно уравнению (3.5), имеем:
Для 1 гири: 
|
| Найти: а - ? Т - ? |
Для 2 гири: 
3. Предположим, что нить невесома и нерастяжима. Выберем элемент нити Dm и запишем уравнение движения в проекции на ось У: 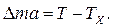 Поскольку Dm = 0, то
Поскольку Dm = 0, то 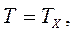 есть сила натяжения нити во всех точках одинакова. Ускорения движения гирь тоже одинаковы,
есть сила натяжения нити во всех точках одинакова. Ускорения движения гирь тоже одинаковы, 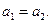 Так как из-за нерастяжимости нити за одно и то же время гири проходят один путь, то есть следовательно,
Так как из-за нерастяжимости нити за одно и то же время гири проходят один путь, то есть следовательно, 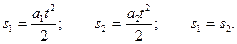
Но направление векторов 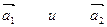 противоположны.
противоположны.
4. И.С.О.: Тело отсчета – Земля; система координат – линейная; ОУ – вертикально вниз.
Для 1 гири: Для 2 гири:
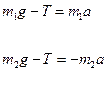
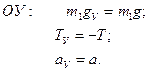
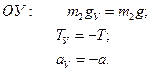
Для 1 гири:
Для 2 гири:
5. Решая совместно полученную систему уравнений относительно искомой величины, можно получить: 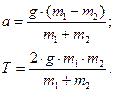

6. Вычисления производим в Международной системе единиц СИ:
1) проверка единиц физических величин измерений справа и слева от знака равно:
2) 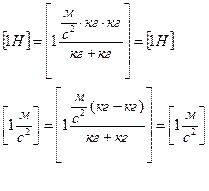
3) вычисления: 
Ответ:Т = 13 Н; а = 3,27  .
.
Задача 3.4. Невесомый блок укреплен на конце стола. Гири 1 и 2 одинаковой массы  = 1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол m =0,1. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением в блоке пренебречь.
= 1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол m =0,1. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением в блоке пренебречь.
   Дано:
= 1 кг
m =0,1 Дано:
= 1 кг
m =0,1
| Решение:
1.
 Рисунок к задаче 3.4.
Рисунок к задаче 3.4.
|
| Найти: а - ? Т - ? |
1. Для 1 гири: 
Для 2 гири: 
2.  И.С.О. : Тело отсчета – Земля; Система координат – Декартова; ОХ – вертикально вниз(по ходу движения гири 1); ОУ – горизонтально влево (по ходу движения гири 2); Начальная координата – в точке О.
И.С.О. : Тело отсчета – Земля; Система координат – Декартова; ОХ – вертикально вниз(по ходу движения гири 1); ОУ – горизонтально влево (по ходу движения гири 2); Начальная координата – в точке О.
3.  ОХ:
ОХ:
 m1 g – T1 = m1a T2 – FТР = m2a
m1 g – T1 = m1a T2 – FТР = m2a
(см. задачу 3.3)
Сила трения равна: 
4. Решая систему уравнений относительно искомой величины:

можно получить: 
5.Вычисления производим в Международной системе единиц СИ:
1) проверка единиц физических величин измерений справа и слева от знака равно:


2) вычисления:

Ответ:а = 4,4  , Т = 5,4 Н.
, Т = 5,4 Н.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1. Два тела, массы которых 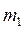 и
и 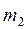 связаны невесомой нерастяжимой нитью и лежат на горизонтальной плоскости. С каким ускорением будут двигаться эти тела, если к телу массой
связаны невесомой нерастяжимой нитью и лежат на горизонтальной плоскости. С каким ускорением будут двигаться эти тела, если к телу массой 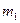 приложить горизонтально направленную силу
приложить горизонтально направленную силу  ? Трением между телом и плоскостью пренебречь.
? Трением между телом и плоскостью пренебречь.
(Ответ: а = F/( 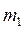 +
+ 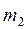 ).
).
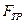 3.2. На автомобиль массой m = 1 тво время движения действует сила , равная 0,1 действующей на него силе тяжести mg. Какова должна быть сила тяги F, развиваемая мотором автомобиля, если автомобиль движется с ускорением а =
3.2. На автомобиль массой m = 1 тво время движения действует сила , равная 0,1 действующей на него силе тяжести mg. Какова должна быть сила тяги F, развиваемая мотором автомобиля, если автомобиль движется с ускорением а =  в гору с уклоном 1 м на каждые 25 м пути.
в гору с уклоном 1 м на каждые 25 м пути.
(Ответ: F = 2,37 кН).
3.3.Найти силу натяжения Т нити в устройстве, изображенном на рисунке, если массы тел 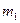 = 100 г и
= 100 г и 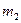 = 300 г.
= 300 г.
 (Ответ: Т = 1,26 Н).
(Ответ: Т = 1,26 Н).
Рисунок к задаче 3.3.
 3.4. Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол a =
3.4. Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол a =  . Гири 1 и 2 одинаковой массы
. Гири 1 и 2 одинаковой массы  = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гири о наклонную плоскость и трением в блоке пренебречь. (Ответ: а = 2,45 ; Т = 7,35 Н).
= 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гири о наклонную плоскость и трением в блоке пренебречь. (Ответ: а = 2,45 ; Т = 7,35 Н).

Рисунок к задаче 3.4.
3.5.Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы a =  и b =
и b =  . Гири 1 и 2 одинаковой массы
. Гири 1 и 2 одинаковой массы  = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
= 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
(Ответ: а = 1,03  Т = 5,9 Н).
Т = 5,9 Н).

Рисунок к задаче 3.5.
3.6.Маляр работает в подвесном кресле (см. рисунок). Вес его 72 кГ. Ему понадобилось срочно подняться вверх. Он принимается тянуть за веревку с такой силой, что его давление на кресло уменьшается до 40 кГ. Само кресло весит 12 кГ. а) Чему равно ускорение маляра и кресла? б) Чему равна полная нагрузка на блок?
(Ответ: N = 2Т = 112 кГ).

Рисунок к задаче 3.6.
3.7.Посмотрите на рисунок. Какую постоянную горизонтальную силу нужно приложить к М, чтобы  и
и  относительно М не двигалось?
относительно М не двигалось?
 (Ответ:
(Ответ:  ).
).
Рисунок к задаче 3.7.
3.8.К потолку лифта, масса которого  , подвешен груз массы
, подвешен груз массы  . Приложенная сила F заставляет лифт двигаться с ускорением вверх (F больше (
. Приложенная сила F заставляет лифт двигаться с ускорением вверх (F больше (  )g). Груз
)g). Груз  находится на расстояние S от пола лифта:
находится на расстояние S от пола лифта:
а) найдите ускорение лифта.
б) чему равно натяжение нити, которой груз привязан к потолку?
в) нить внезапно оборвалась. Чему равно ускорение лифта и груза  в следующий момент?
в следующий момент?
(Ответ:  ).
).
3.9.Космический путешественник собирается отправиться на Луну. У него есть пружинные весы и гиря А массой 1 кг. Если подвесить эту гирю на пружине весов на Земле, они покажут 1 кГ. Опустившись на некотором участке лунной поверхности, где ускорение силы тяжести точно не известно (известно лишь, что оно примерно в шесть раз меньше, чем на Земле), космонавт подбирает камень В, который вытягивает на весах тот же самый 1 кГ. Затем он подвешивает А и В на нити, перекинутой через блок, как показано на рисунке, и обнаруживает, что камень опускается с ускорением 1,2 м/сек2. Чему равна масса камня В?
(Ответ: m = 5,75 кг).

Рисунок к задаче 3.9.
3.10.Двое молодых марсиан, Паоло и Франческа, хотят переправиться через марсианский канал Римини, но ни одна гондола не берет их обоих сразу, а переправляться в разных лодках они отказались. Находчивый гондольер Джузеппе умудряется все-таки заработать на их переезде. Он подвешивает эту парочку на мачте (см. рисунок) с помощью невесомых и абсолютно гладких блоков и веревок (характерная особенность всех марсианских конструкций) и быстро переправляет влюбленных через канал, пока ни один из них не успевает коснуться ни мачты, ни палубы. Много ли при этом Джузеппе выигрывает в нагрузке? Напоминаем: натяжение невесомой нити, перекинутой без трения через невесомый блок, одинаково с обеих сторон блока.
(Ответ: N = 116 кГ; DN = 34 кГ).

Рисунок к задаче 3.10.