А через два года

FV = 1000 + 400 + 400 = 1800 грн.

Таким образом, общая формула начисления простых процентов имеет следующий вид

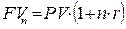. (4. 3)

В формуле (4.3) n может иметь дробное значение, когда речь идет о части периода (года), например, если банк выдал ссуду на t дней, а в году 365 дней, то

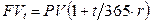. (4.3')

Кредитная сделка может производиться при изменяющейся процентной ставке. В этом случае существует некоторая временная решетка процентной ставки

n1	n2	n3	…	ni
r1	r2	r3	…	ri

и наращение производиться по формуле

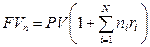, (4.3")

где N – общее количество значений в решетке;

n_i – общее количество периодов, в течение которых действует процентная ставка r_i .

Дисконтирование при простых процентах осуществляется с помощью формулы, которая получается путем обращения (4.3):

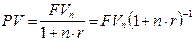. (4.4)

Проиллюстрируем феномен дисконтирования с помощью следующего примера. Вы собирается накопить 50000 грн. в течение года посредством банковского депозита, который предлагает ежемесячное начисление простых процентов по месячной процентной ставке 5%. Какую сумму необходимо положить на депозит?

Из формулы (4.4) следует

.

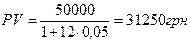Наращение и дисконтирование с помощью учетной ставки. В некоторых случаях в качестве базы для оценки доходности финансового инструмента используется не современное, а будущее значение. В этом случае норма доходности называется учетной ставкой (а не процентной ставкой). Наиболее распространенной областью применения учетной ставки является учет векселей. Суть учетной ставки состоит в том, что доход инвестора начисляется на сумму, подлежащую к оплате в конце срока кредитования, а не на начальную сумму.

Формулу для учетной ставки получим по аналогии в формулой для процентной ставки.

Для процентной ставки из формулы (4.3) получим:

По аналогии определим учетную ставку d, как следующее отношение

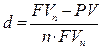
Отсюда легко следует формула для дисконтирования в случае использования учетной ставки для схемы простых процентов.

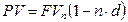. (4.5)

Формула для наращения с использованием учетной ставки получается путем обращения формулы для дисконтирования:

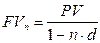. (4.6)

 

Пример. Переводной вексель, тратта, выдан на сумму 100 тыс. грн. с уплатой по векселю 25 апреля. Держатель векселя учел его в банке 11 февраля. На этот момент учетная ставка по векселям в этом банке составляла 12%. Определить величину дисконта, которую банк произвел в момент учета векселя и сумму, которую получил держатель векселя.

Сопоставляя даты учета и погашения векселя, определим, что до погашения осталось 73 дня. Таким образом, дисконт по векселю составит

D = 100000 · 73 / 365 · 0.12 = 2400 грн.,

а владелец векселя (теперь уже бывший) получит

PV =100000 – 2400 = 97600 грн.

Сравним результаты дисконтирования с использованием учетной и процентной ставок. Для этого воспользуемся формулой для дисконтирования

,

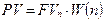в которой множитель дисконтирования будем вычислять следующим образом:

· для процентной ставки

,

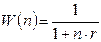· для учетной ставки

.

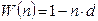Результаты сравнения представлены в таблице.

n	1/12	1/4	1/2
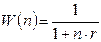
	0,99174	0,9756	0,9524	0,9091	0,833	0,667	0,5
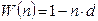
	0,99167	0,975	0,95	0,9	0,8	0,5

 

При дисконтировании с помощью учетной ставки возникает методический парадокс: дисконтированное значение может стать 0 или даже отрицательным. На практике такого не бывает, так как вексель исключительно краткосрочный инструмент заимствования.

Сложные проценты. Сложным процентом называется сумма дохода, которая образуется в результате инвестирования денег при условии, что сумма начисленного простого процента не выплачивается в конце каждого периода, а присоединяется к сумме основного вклада и в следующем платежном периоде сама приносит доход.

При норме доходности r имеем:

· в первый год: ,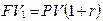

· во второй год: 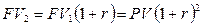и т. д.

Таким образом, общая формула для начисления сложных процентов имеет следующий вид

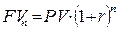. (4.7)

Настоящее (современное) значение стоимости определенной будущей суммы денег вычисляется с помощью формулы

 

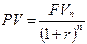. (4.8)

 

Если процентная ставка изменяется в различные периоды времени, т.е.

 

n			…	n
r	r1	r2	…	rn

 

В этом случае формулы (4.7) и (4.8) обобщаются следующим образом:

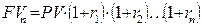или

. (4.7')

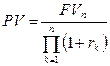. (4.8')

Рассмотрим соотношение между показателями наращения для простых и сложных процентов. С помощью простых алгебраических рассуждений нетрудно установить,

· если n < 1 года, то , инвестировать при простых процентах более выгодно,

· если n ³ 1 года, то 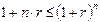, то предпочтительней для инвестора является схема сложных процентов.

 

Пусть проценты начисляются т раз в году, тогда процентная ставка в пересчете на период будет равна r/m, а количество периодов будет равным nm. В соответствии с исходной формулой (4.3) в этом случае наращение будет производиться с помощью следующего соотношения:

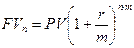. (4.9)

Формула для вычисления настоящей стоимости также принимает следующий обобщенный вид:

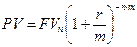. (4.10)

 

Пример. Что более выгодно при вложении денег на 2 года: процентная ставка 40% годовых при начислении процентов 2 раза в год, либо ставка 38% годовых, начисляемых 12 раз в год?

Рассчитаем показатель наращения с помощью формулы (4.9):

,

.

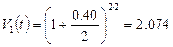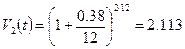Очевидно, что второй вариант предпочтительней.

Для сравнения эффективности вложения денег при различном количестве начислений процентов в году вводят понятие эффективной процентной ставки: это процентная ставка такого вложения денег, при котором начисление процентов происходит только 1 раз в конце года и это равносильно по конечному результату конкретной схемы начисления процентов, для которой определяется эффективная процентная ставка.

По определению эффективной процентной ставки имеем одну и ту же величину будущего значения денег, полученных

· при начислении процентов m раз в году при номинальной процентной ставке r,

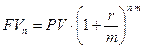и

· при начислении процентов один раз в году при процентной ставке r_э:

.

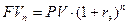Следовательно

,

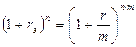откуда легко следует

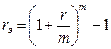. (4.11)

Влияние числа начислений процентов на эффективность инвестирования денег при неизменной годовой процентной ставке иллюстрируется ниже.

 

m
rэ	30%	32,3%	33,6%	34,5%	35%

 

Наращение и дисконтирование производится с использованием учетной ставки по схеме сложных процентов производится аналогично, но расчетные формулы отличаются. С помощью простых рассуждений можно доказать, что

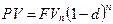. (4.12)

Если начисление процентов производится т раз в году, то формула (12) будет иметь вид

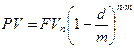. (4.12')

Формулы для наращения при использовании учетной ставки легко получаются из формул дисконтирования путем простого обращения последних:

 

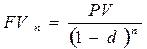, (4.13)

 

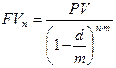. (4.13')

 

Пример. Вексель на 500 тыс. грн. учитывается банком по учетной ставке 15% при начислении процентов 12 раз в году. Вексель учитывается за 8 месяцев до погашения. Необходимо определить величину дисконта.

return false">ссылка скрыта

Воспользовавшись формулой (4.12') получим

.

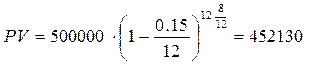Следовательно, дисконт составляет 500000 – 452130 = 47870 грн.