Локальная теорема Лапласа
Локальная теорема Лапласа определяет вероятность того, что в серии из n повторных независимых испытаниях событие А наступит точно k раз, при условии, что вероятность наступления события А в каждом испытании постоянна и равна р. Если число испытаний невелико n<10, то применяют формулу Бернулли. Если же n велико, то для удобства вычислений применяют локальную теорему Лапласа:
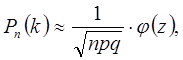(1.22)
Значения функции Гаусса 
находятся из таблиц распределения (приложение 1) для каждого значения аргумента z, вычисляемого по формуле:
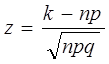. (1.23)
Функция Гаусса четная, то есть φ(-z)=φ(z).