Формула Бернулли

 

Для определения вероятности того, что событие А в n повторных независимых испытаниях появится точно k раз, применяется формула Бернулли:

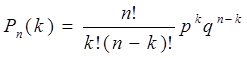, (1.20)

где n – число испытаний;

k – число наступления события А в n испытаниях;

р – вероятность наступления события А в каждом отдельном испытании;

q = 1-p – вероятность наступления события, противоположному А, в одном испытании.

Произведение N натуральных чисел 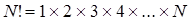называется факториалом, 0!=1.

Числом сочетаний n по k называется величина:

.

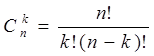Тогда формула Бернулли примет вид:

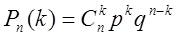. (1.20.1)

Определение.Число наступлений события А в n повторных независимых испытаниях называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями других возможных исходов.

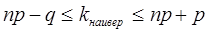. (1.21)

Пример 1.7. 25% большой партии костюмов составляют костюмы 48 размера. Найти наивероятнейшее число костюмов 48 размера среди серии из шести отобранных наугад и вычислить соответствующую этому вероятность. Вычислить вероятность того, что среди костюмов этой серии хотя бы один будет 48 размера.