Для ликвидации ЧС по федеральным округам, млн. рублей
Приложение 10
Некоторые способы обработки
и представления результатов исследования
Исследователь на определенном этапе своей научной работы встречается с необходимостью проверки выдвинутых гипотез, эффективности выполненных разработок. Критерием результативности проведенной работы, справедливости сделанных выводов является качественная математико-статистическая обработка результатов эксперимента.
Наиболее простым случаем является случай, когда сложное задание можно разделить на элементы, однородность которых не вызывает сомнений. При этом можно найти индивидуальные коэффициенты полноты выполнения задания по формуле:
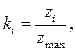
где - zi – число элементов задания, выполненных i- м учащимся,
z max - число элементов задания, которые мог бы выполнить этот учащийся.
Пример: Ученик должен был заучить 40 слов. Во время терминологического диктанта он воспроизвел 30 слов. Его
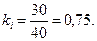
Если задание выполняется группой учащихся, для дальнейших расчетов необходимо найти среднее значение коэффициента полноты выполнения задания и посмотреть, как отклоняются от среднего значения индивидуальные коэффициенты полноты выполнения задания.
Среднее значение коэффициента полноты выполнения задания находится по формуле:
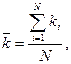
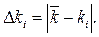 где N – число учащихся, выполнявших задание.
где N – число учащихся, выполнявших задание.
Модуль отклонения
Пример:В таблице 1 приведены гипотетические значения коэффициентов полноты выполнения некоторого задания группой учащихся.
Таблица 1
| № | |||||||||
| ki | 0,32 | 0,35 | 0,40 | 0,47 | 0,50 | 0,53 | 0,60 | 0,65 | 0,68 |
Обратите внимание на то, что ряд значений ki упорядочен!
Исходя из предположения, что результаты тестирования являются случайными величинами, найдем среднее значение коэффициента полноты выполнения задания.
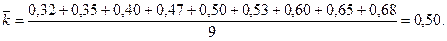
Зная среднее значение коэффициента полноты выполнения задания, можно показать, как откланяются от него индивидуальные коэффициенты, и сравнить каждый индивидуальный коэффициент со средним значением. Последнюю задачу можно решить путем вычитания модулей отклонения индивидуальных коэффициентов полноты выполнения задания от среднего: 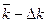 .
.
В таблице 2, отображены соответствующие значения указанных величин.
Таблица 2
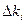
| 0,18 | 0,15 | 0,10 | 0,03 | 0,03 | 0,10 | 0,15 | 0,18 | |
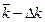
| 0,32 | 0,35 | 0,40 | 0,47 | 0,50 | 0,47 | 0,40 | 0,35 | 0,32 |
Когда проводится оценка результатов выполнения контрольной работы группой учащихся, наряду со средним значением коэффициента полноты выполнения заданий, рассчитывается величина разброса результатов, которая имеет самостоятельное значение. Это видно из такого примера.
В двух классах средние коэффициенты полноты выполнения контрольной работы составляют 0,6. Но в первом классе половина класса выполнила работу полностью (k1=1), а половина класса имела коэффициент k2=0,2. Во втором классе 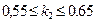 у всех учащихся коэффициент полноты выполнения работы лежит в интервале . Понятно, что результаты выполнения работы в этих классах принципиально отличаются друг от друга и требуют различных способов анализа и корректировки.
у всех учащихся коэффициент полноты выполнения работы лежит в интервале . Понятно, что результаты выполнения работы в этих классах принципиально отличаются друг от друга и требуют различных способов анализа и корректировки.
Разброс результатов можно посчитать следующим способом. По этому способу находится величина, называемаядисперсией:
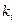
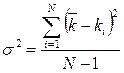
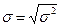 (На надо смотреть как на случайные величины). Если N>30, то деление производится на N.
(На надо смотреть как на случайные величины). Если N>30, то деление производится на N.
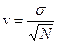 Квадратный корень из дисперсии называется средним квадратичным, или стандартным отклонением, а
Квадратный корень из дисперсии называется средним квадратичным, или стандартным отклонением, а
величина - коэффициентом вариации.
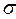 Чем меньше , тем острее пик нормального распределения.
Чем меньше , тем острее пик нормального распределения.
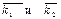 Зная средние значения коэффициентов полноты выполнения контрольной работы из двух выборок , дисперсии
Зная средние значения коэффициентов полноты выполнения контрольной работы из двух выборок , дисперсии 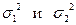 , число человек, выполнявших работы
, число человек, выполнявших работы 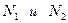 , можно сравнить результаты между собой. Для этого находится экспериментальное значение коэффициента Стьюдента
, можно сравнить результаты между собой. Для этого находится экспериментальное значение коэффициента Стьюдента 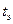 :
:
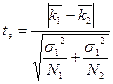
и число степеней свободы 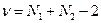 .
.
Критерий Стъюдента используют для сравнения средних значений двух случайных величин в предположении, что обе имеют нормальное распределение.
Далее по специальным таблицам (см. табл. 3), которые имеются в справочниках по математике в разделе «Математическая статистика», находится теоретическое значение коэффициента Стьюдента 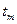 для соответствующего числа степеней свободы и интересующей исследователя степени значимости результата Р.
для соответствующего числа степеней свободы и интересующей исследователя степени значимости результата Р.
Например, для 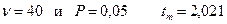 .
.
Если оказывается, что 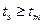 , делают вывод: на уровне значимости 0,05 (или на 5% уровне значимости, или с достоверностью 95%) между результатами выборок существует статистически значимая разница. В противном случае делать вывода о различии результатов нельзя.
, делают вывод: на уровне значимости 0,05 (или на 5% уровне значимости, или с достоверностью 95%) между результатами выборок существует статистически значимая разница. В противном случае делать вывода о различии результатов нельзя.
Таблица 3
| t – распределение Стьюдента | |||||||
| P V | 0,80 | 0,40 | 0,20 | 0,10 | 0,05 | 0,02 | 0,01 |
| 0,325 | 1,376 | 3,078 | 6,314 | 12,706 | 31,821 | 63,657 | |
| 0,289 | 1,061 | 1,866 | 2,920 | 4,303 | 6,965 | 9,925 | |
| 0,277 | 0,978 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | |
| 0,271 | 0,941 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | |
| 0,267 | 0,920 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | |
| 0,265 | 0,906 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | |
| 0,263 | 0,896 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | |
| 0,262 | 0,889 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | |
| 0,261 | 0,883 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | |
| 0,260 | 0,879 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | |
| 0,260 | 0,876 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | |
| 0,259 | 0,873 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | |
| 0,259 | 0,870 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | |
| 0,258 | 0,868 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | |
| 0,258 | 0,866 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | |
| 0,258 | 0,865 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 | |
| 0,257 | 0,863 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | |
| 0,257 | 0,862 | 1,330 | 1,734 | 2,101 | 2,552 | 2,878 | |
| 0,257 | 0,861 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | |
| 0,257 | 0,860 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | |
| 0,257 | 0,859 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 | |
| 0,256 | 0,858 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | |
| 0,256 | 0,858 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 | |
| 0,256 | 0,857 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 | |
| 0,256 | 0,856 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 | |
| 0,256 | 0,856 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 | |
| 0,256 | 0,855 | 1,314 | 1,703 | 2,052 | 2,473 | 2,771 | |
| 0,256 | 0,855 | 1,313 | 1,701 | 2,048 | 2,467 | 2,763 | |
| 0,256 | 0,854 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 | |
| 0,256 | 0,854 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 | |
| 0,255 | 0,851 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 | |
| 0,254 | 0,848 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 | |
| 0,254 | 0,845 | 1,289 | 1,658 | 1,980 | 2,358 | 2,617 |
Приложение 11