Глава 4. КРУЧЕНИЕ

 

При кручении в поперечном сечении стержня возникает крутящий момент М_К. Нагрузкой при кручении являются скручивающие моменты m_i, действующие относительно продольной оси стержня. Крутящий момент определяется методом сечений и равен алгебраической сумме внешних (скручивающих) моментов, действующих на рассматриваемую часть стержня: М_К = ∑m_i. Момент считается положительным, если он направлен против хода часовой стрелки (при взгляде со стороны сечения).

При кручении в поперечном сечении стержня возникают касательные напряжения τ. Касательные напряжения τ распределяются по площади круглого поперечного сечения стержня неравномерно, нарастая от оси вала к поверхности по линейному закону, наибольшие напряжения возникают по контуру сечения. Закон распределения напряжений τ вдоль произвольного радиуса в сечении изображен на рис. 13. Во всех точках окружности радиуса ρ напряжение τ = const и направлено по касательной к этой окружности. Напряжения τ в сечении сводятся к крутящему моменту М_К(рис.13):

М_К = .

Формула для определения τ имеет вид

,

 

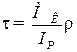где I_p – полярный момент инерции сечения, м⁴; для сплошного круглого сечения 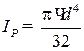(прил. 4);

М_К – крутящий момент, Н·м.

 

 

Рис. 13. Распределение касательных напряжений

в сечении при кручении

Условие прочности имеет следующий вид:

,

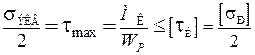где – геометрическая характеристика прочности при кручении, называемая полярным моментом сопротивления, м³;

[τ_к] – допускаемое напряжение на кручение, Па.

Для сплошного круглого сечения (рис. 14)

.

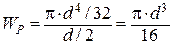Рис.14. К определению полярного момента сопротивления W_p

длясплошного круглого сечения

Для полого толстостенного цилиндра (рис. 15)

.

 

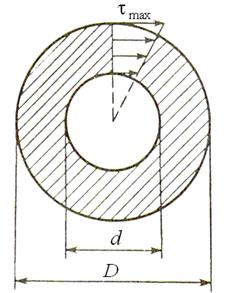
Рис. 15. К определению полярного момента сопротивления W_p

дляполого толстостенного цилиндра

Деформация при кручении характеризуется углом закручивания на единицу длины стержня θ:

.

Величина θ называется относительным углом закручивания и имеет размерность рад/м.

Условие жесткости имеет вид

,

где G – модуль упругости материала при сдвиге, Па.

Зависимость между модулями упругости Е и G имеет вид

,

где μ – коэффициент Пуассона;

[θ] – допускаемый относительный угол закручивания на единицу длины стержня (рад/м).

Диаметр стержня, работающего на кручение, определяется из двух условий: прочности и жесткости. Во внимание берется наибольший диаметр. Окончательное значение его принимается согласно стандарту.

 

Пример 4

 

Определить диаметры поперечных сечений участков стержня (вала) (рис. 16, а), если [τ_K] = 100 МПа, G = 80 ГПа, [θ] = 1,5^о/м. Построить эпюру углов поворота сечений φ.

[θ] = 1,5^о/м = рад/м.

Рис.16. Построение эпюр крутящих моментов М_к

и углов поворота сечений φ:

а – расчетная схема; б – эпюра крутящих моментов М_к;

в – эпюра углов поворота сечений φ

Должно выполняться условие равновесия ∑m_x = 0:

∑m_x = m₁ – m₂ – m₃ + m₄ = 2 – 1 – 4 + 3 = 0.

Для определения крутящих моментов М_к на участках стержня будем рассматривать левую часть его.

Участок I: М_KI = m₁ = 2 кН·м.

Участок II: М_KII = m₁ – m₂ = 2 – 1 = 1 кН·м.

Значение М_КIII определите самостоятельно (М_КIII = – 3 кН·м).

По вычисленным значениям М_к строится эпюра (см. рис. 16, б).

Преобразуем условия прочности и жесткости к виду, удобному для определения диаметра стержня.

Условие прочности:

, .

Условие жесткости:

,

откуда

.

Вычисляем диаметр вала из условий прочности и жесткости.

На первом участке:

– диаметр вала из условия прочности

;

– диаметр вала из условия жесткости

.

 

Принимаем d₁ = 6 см.

На втором участке:

– диаметр вала из условия прочности

;

– диаметр вала из условия жесткости

.

Принимаем d₂ = 5 см.

Диаметр поперечного сечения на участке III рассчитайте самостоятельно (d₃ = 5,35 см, d^’₃ = 6,18 см, принимаем d₃ = 7 см).

Если стержень имеет постоянное сечение, то диаметр его определяется исходя из максимального значения М_к.

Определим деформации участков стержня:

.

Значения φ на других участках следующие:

.

Углы поворота характерных сечений (границ участков) равны:

;

.

Значение φ_D определите самостоятельно (φ_D = – 0,429^о).

Эпюра углов поворота сечений показана на рис. 16, в.

Вычислим максимальные напряжения на участках стержня:

Вычисленные значения диаметров участков стержня обеспечивают его прочность и жесткость.