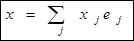В противном случае система противоречива.
I j k
1 0 0
0 1 0
0 0 1
Ещё раз обращаем внимание: у нас векторы – это столбцы. Любой другой трёхмерный вектор выражается через эти орты в виде линейной комбинации a= 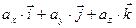 , а числа аi –это проекции вектора a на оси координат Oxyz. Это именно те числа, которые находятся в векторе-столбике. Определитель матрицы такого базиса равен единице.
, а числа аi –это проекции вектора a на оси координат Oxyz. Это именно те числа, которые находятся в векторе-столбике. Определитель матрицы такого базиса равен единице.
Дальше в задачах нам потребуется переходить от записи вектора в одном базисе к записи этого же вектора в другом базисе. Делается это следующим образом( n=3).
| Разложим новый базис по старому: | ||||||||||||
Назовём базис  старым, а базис старым, а базис  - новым. - новым.
| 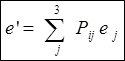
| |||||||||||
| Оба базиса считаем заданными. Разложим вектора нового базиса по старому базису: по формуле (2'), (но в других обозначениях: вместо xi пишем e'i) | Эти формулы в матричном виде можно записать кратко | |||||||||||
 = p11· = p11· 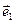 +p12· +p12·  +p13· +p13· 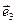
| ||||||||||||
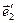 = p21· = p21· 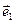 +p22· +p22·  +p23· +p23· 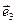
| ||||||||||||
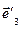 = p31· = p31· 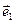 +p32· +p32·  +p33· +p33· 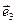
| ||||||||||||
 Кратко это можно записать в виде (3) Кратко это можно записать в виде (3)
| ||||||||||||
| Коэффициенты этих разложений составляют квадратную матрицу P. Она вычисляется. Т.к. новые базисные векторы линейно независимы, то определитель её отличен от нуля. Разложим произвольный вектор x по старому и новому базисам. |
| В новом базисе | 
| |||||||||
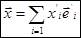 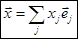
| ||||||||||||
| Подставляя во вторую формулу разложение (3) и | ||||||||||||
сравнивая эти разложения найдём, что компоненты вектора xв старом базисе
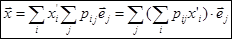 выражаются все по формулам выражаются все по формулам
| ||||||||||||
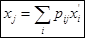 Сравнивая это с первой формулой из (4) получим Сравнивая это с первой формулой из (4) получим
| 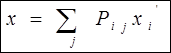
| |||||||||||
| или в подробной записи | ||||||||||||
| Видно, что матрица перехода транспонировалась. Запишем это в покомпонентной записи: | ||||||||||||
| x1=p11·x'1+p21·x'2+p31·x'3 | ||||||||||||
| x2=p12·x'1+p22·x'2+p32·x'3 | ||||||||||||
| x3=p13·x'1+p23·x'2+p33·x'3, | ||||||||||||
| и в матричной записи x=PTx'. Обращаем внимание на операцию транспонирования. | ||||||||||||
| Формулы выражают старые координаты вектора x через его новые координаты | ||||||||||||
| и представляют собой линейное преобразование переменных x в x'. | ||||||||||||
| Обратное преобразование проделывается аналогично, но с матрицей ( PT)-1 x'=(PT)-1x | ||||||||||||
| Пример такого преобразования базисов приведён в файле к этой лекции на диске. |
return false">ссылка скрыта
В евклидовом пространстве En определено скалярное произведение двух векторов одинаковой размерности:
(xT*y)= 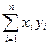 =x1·y1+x2·y2+…+xn·yn c – это скаляр. (3)
=x1·y1+x2·y2+…+xn·yn c – это скаляр. (3)
Здесь в записи формулы используется операция транспонирования: вектор строка умножается на вектор столбец.
Но умножение в другом порядке (y*xT) - это уже не скаляр, не вектор, а квадратная матрица А=(Aij), элементами которой являются Aij =yi*xj. Эти две операции умножения (xT*y) и (y*xT) в принципе различны, так что писать, особенно в аналитических вычислениях нужно правильно - так, как в (3).
Если (xT*y)=с=0, то векторы x и y называются ортогональными (обобщение термина перпендикулярности).
Уже в следующей лекции – в линейном программировании (ЛП) - нам потребуется другая интерпретация формулы (3). В более привычных обозначениях
y=(cT·x)=c·x1+c2·x2+….+cn·xn (3')
Это выражение называется линейной формой с независимыми переменными xi и постоянными сi. Интересным с точки зрения (ЛП) является для нас то, что скалярное произведение, как мы показали выше, имеет в разных базисах разное численное значение.
Если приравнять (3') к нулю
y=(cT·x)=c1·x1+c2·x2+….+cn·xn= 0, (3'')
то это становится уравнением и геометрически это уравнение можно представлять как (n-1)-мерные гиперплоскости в n-мерном пространстве: все векторы xразмерности n, удовлетворяющие (3'') лежат в этой гиперплоскости. Эти гиперплоскости проходят через начало координат. В двумерном пространстве это прямые линии, в трёхмерном - плоскости, проходящие через начало координат, т.к. в уравнении нет свободного члена иx=0 удовлетворяет уравнению (3''). Числа ci в определении гиперплоскости– это компоненты вектора нормали к этой плоскости. Они же являются компонентами вектора градиента линейной функции y=f(x), определяемой (3''). Эти компоненты, естественно, константы, т.к. функция линейна, а ci=const. Всё это разные взгляды на один и тот же предмет: скалярное произведение векторов.
Множество всех векторов x,удовлетворяющих неравенству y=(cT·x)=c1·x1+c2·x2+….+cn·xn ≥ b, называется положительным полупространством.
Множество, представляющее собой пересечение конечного числа разных гиперплоскостей и полупространств называется многогранным множеством в En . Можно показать, что это множество выпукло. Поэтому это множество есть просто выпуклый многогранник. Область допустимых решений в линейном программировании задаётся типичным многогранником S={x:Ax=b,x≥0} или S={x:Ax≤b, x≥0}. Известно, что почти любая точка xиз этого множества может быть представлена как выпуклая комбинация двух любых других точек x1 и x2: 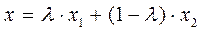 ,
,  . Точки, которые не могут быть так представлены, называются крайними. Это вершины многогранника. В ЛП мы будем называть их опорными планами. Один из этих планов будет оптимальным решением задачи ЛП. Структура вектора крайних точек имеет (двухэтажный) вид:
. Точки, которые не могут быть так представлены, называются крайними. Это вершины многогранника. В ЛП мы будем называть их опорными планами. Один из этих планов будет оптимальным решением задачи ЛП. Структура вектора крайних точек имеет (двухэтажный) вид:
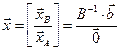 , B-1b≥0
, B-1b≥0
где B- квадратная невырожденная матрица размерности m*m, выделенная из матрицы А с помощью перестановок столбцов к виду [B,N], 0- нулевой вектор размерности (n-m). Как следствие отсюда вытекает, что максимальное количество крайних точек в многограннике конечно и равно числу возможных способов выбора из n столбцов по m, т.е. равно числу сочетаний из n по m: 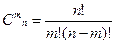 .
.
Теперь о матрицах.
Матрица A– это n*m чисел аi,j, упорядоченных в прямоугольную или квадратную (при n=m) таблицу из n строк и m столбцов. Индекс i нумерует строки, i=1,2, … n; индекс j нумерует столбцы j=1,2, …m. Количество строк и столбцов определяет размерность матрицы. Иногда эти числа указывают как порядок матрицы. Например, матрица порядка А2*3. Это матрица из двух строк и трёх столбцов. Или говорят, например, дана квадратная матрица второго порядка, т.е. порядка А2*2.
Для матриц, в том числе и для прямоугольных, определена операция транспонирования: это замена строк матрицы на её столбцы (АT)ij = Aji. (A*B)T = (BT*AT). Т.е. первый столбец в матрице Аявляется первой строкой в матрице АТ, второй столбец – второй строкой и т.д.
Матрицу An*m можно представить как систему m штук n-мерных векторов и записать в виде
A= (a1,a2,…am), (3''')
где a1,a2,…am- векторы-столбцы размерности n. То же самое можно говорить и строках матрицы. В этом случае число векторов равно n, a1,a2,…an, а размерность их равна m. Представлять матрицу в том или ином виде – вопрос удобства и содержательной постановки. Технически – это операция транспонирования. Но, как мы увидим, операция транспонирования имеет и более глубокий смысл.
Для матриц определены некоторые арифметические операции, которые вам знакомы:
-две матрицы равны, если они имеют одинаковую размерность и если равны их матричные элементы.
-определена сумма матриц одинаковой размерности, умножения матрицы на вектор и умножение матрицы на матрицу.
Квадратной матрице поставлено в соответствие число, называемое определителем матрицы det(A), которое вычисляется по известным из школы методам. Если det(A)≠0, то столбцы матрицы представлении (3''') образуют систему линейно независимых векторов. То же можно сказать и про строки матрицы. Но определитель может быть равен нулю. В этом случае матрица называется вырожденной.
Важным понятием в теории матриц является ранг матрицы rang(A)=r. Понятие ранга относится как к квадратным, так и к прямоугольным матрицам. Ранг матрицы А – это наибольший порядок квадратной подматрицы А, определитель (минор) которой не равен нулю. Ранговый минор называется базисным минором. Столбцы/строки прямоугольной матрицы, пересекающие базисный минор являются линейно независимыми и любой небазисный столбец/строка матрицы выражается в виде линейной комбинации базисных. Ранг определяет максимальное количество линейно независимых строк (и тем самым) столбцов матрицы. Если ранг квадратной матрицы равен её размерности, то матрица называется матрицей полного ранга.
Матрицу можно умножать на вектор и на другую матрицу. Результатом умножения матрицы Аразмерностьюnстрок и m столбцов на m-мерный вектор x,будет n-мерный вектор т.е.
A*x = b.(Anm*xm= bn)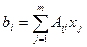 ,i=1,2,…n. (4)
,i=1,2,…n. (4)
Индекс i нумерует строки, а индекс j- столбцы. Для остальных случаев размерности операция умножения матрицы на вектор не определена и, следовательно, невозможна.
Если рассматривать формулу (4) как действие некоторого оператора Ана вектор, то результат этого действия очень интересен. Исходный вектор x
а) при m=n остаётся в своём m-мерном пространстве, но при этом поворачивается и меняет свою длину.
б) при m≠n вектор xпереходит в пространство другой размерности.
в) если же не известно, какой вектор x переходит в результате преобразования в заданный вектор b, то для нахождения x следует решить систему уравнений (4).
 Умножение двух матриц определено только для случая, когда количество столбцов m в матрицеА равно количеству строк n в матрицеB
Умножение двух матриц определено только для случая, когда количество столбцов m в матрицеА равно количеству строк n в матрицеB
(C)ij=(А*B)ij = 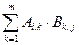 (5)
(5)
Действие деления в векторно-матричном аппарате заменяется умножением А на т.н. обратную матрицу A-1.
A-1*A= A*A-1 =1.
Обратная матрица определена только для квадратных матриц, определитель которых det(A)≠0. При этом роль единицы играет диагональная единичная матрица.
Квадратные матрицы, имеющие обратную, называются невырожденными. Определитель обратной матрицы det(A-1)=1/ det(A). Для обратной матрицы справедливо (A*B)-1= (B-1*A-1). Для того, чтобы матрица была невырожденной необходимо, чтобы её векторы-столбцы были линейно независимы, rang=n
Матрица называется симметричной, если АT = A.Это, конечно, только для квадратных матриц. В математическом программировании симметричные матрицы появляются естественным образом, при векторной записи разложения в ряд Тейлора функции, зависящей от многих переменных. Это является следствием того, что перекрёстные производные от функции нескольких переменных не зависят от порядка дифференцирования
Матрица называется ортогональной, если все её векторы-столбцы ортогональны попарно, т.е. если xТi*xj = 0 при i≠j. Если же еще и xТi*xi= 1 , то матрица называется ортонормированной. Кратко свойство ортонормированности записывается так: xТi*xj = δij , где т.н. дельта-символ равен 1 при i=j и равен 0, при i≠j. Для ортонормированной матрицы
А.АТ= АТ.А =1.
Симметричную ортонормированную матрицу можно всегда привести к диагональному виду. Это используется при решении задач линейной алгебры.
Составим с помощью симметричной матрицы однородный квадратичный многочлен из компонент вектора по формуле:
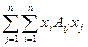 =c
=c
Или в векторном виде:
xT*A*x= (xT*A)Т*x = с. (6)
Это выражение называется квадратичной формой для матрицы А, в отличие от линейной формы cT*x.Хотя и та и другая являются просто скаляром. Отличие же заключается в том, что в квадратичной форме постоянными являются матричные элементы - числа aij.
Матрица называется положительно определённой, если xT*A*x>0 для любых ненулевых векторов x из En. Это понятие играет важнейшую роль в оптимизации, точнее в математическом программировании.
Пока теории достаточно. Определены ещё много свойств и действий с матрицами и векторами, но нужно сказать, что принципиально матричный аппарат не является необходимым. Он просто экономит мел и бумагу, но сильно расходует «серое» вещество. Ведь в конечном случае в вычислениях всё сводится к арифметическим операциям сложения и умножения. Но, с другой стороны, этот аппарат настолько сильно привязан к наукам, особенно к естественным, что без него они уже не представимы.
Скоро нам придётся решать системы линейных уравнений (СЛАУ). Поэтому немного о погрешностях вычислений.
В оптимизации нам придётся иметь дело с векторами и матрицами, как в теоретических формулах, так и при практических вычислениях. Например, для начала, оценивать погрешность (точность) решений в задачах. Для этого нужно договориться, как-то сравнивать между собой векторы и матрицы по величине, т.е. определять, что больше или меньше. Сделать это так же просто, как для сравнения скаляров, нельзя. У вектора много компонент. Для этого в теории матриц вводится понятие нормы вектора и нормы матрицы. Норма вектора xв En определяется по-разному и это зависит во многом от удобства в решаемой задаче. Чаще всего используются норма: ||x ||2=|x|= 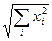 , называемая евклидовой нормой вектора x. Норма вектора это скаляр. Так определённая норма вектора - это просто «длина» вектора. И какой вектор длиннее, тот и больше. И теперь, например, если имеется вектор x – точное решение какой-либо задачи и x’- его приближённое значение, то можно говорить о погрешности решения ∆xabc =||x – x’|| или относительной погрешности || δxотн||=||x – x’||/||x||. Эти погрешности тоже скалярные величины. Но точность оценки векторов и матриц будет уже другая, нежели для чисел. Не так как в оценке точности числа, а грубее, говорят - по норме, для всех компонентов вектора сразу.
, называемая евклидовой нормой вектора x. Норма вектора это скаляр. Так определённая норма вектора - это просто «длина» вектора. И какой вектор длиннее, тот и больше. И теперь, например, если имеется вектор x – точное решение какой-либо задачи и x’- его приближённое значение, то можно говорить о погрешности решения ∆xabc =||x – x’|| или относительной погрешности || δxотн||=||x – x’||/||x||. Эти погрешности тоже скалярные величины. Но точность оценки векторов и матриц будет уже другая, нежели для чисел. Не так как в оценке точности числа, а грубее, говорят - по норме, для всех компонентов вектора сразу.
Для евклидовой нормы вектора выполняется неравенство треугольника: сумма длин двух сторон больше длины третьей стороны. Если обобщить это на n-мерное пространство, то ||x+y||<=||x||+||y||.
Аналогично норме вектора, т.е. тоже формально, определяется норма матрицы. При этом определение нормы матрицы обычно согласовывают с нормой вектора. Это необязательно, но удобно во многих задачах, а в нашей теории оптимизации и решении систем линейных уравнений (СЛАУ) особенно. Поэтому евклидовой норме вектора будем ставить в соответствие связанную (индуцированную) с ней матричную норму ||A||2=(∑∑|xi,j|2)0.5. Для матричных норм выполняется неравенство Шварца ||A*B||≤||A||*||B||.
Системы линейных уравнений.
Огромное разнообразие видов матриц с их характерными свойствами порождает удивительно богатый мир матричной математики, пригодной для построения математических моделей для разных прикладных задач. Наиболее известным разделом является линейная алгебра. Эта ветвь математики, как никакая другая, самым тесным образом переплелась с многочисленными приложениями математики, являясь в них незаменимым инструментом исследования. Она потребуется и в методах оптимизации и прежде всего в линейном программировании.
Вспомним кое-что из линейной алгебры. В линейной алгебре имеется, в сущности, всего одна задача: решить систему линейных алгебраических уравнений
A*x=b, (7)
где А и b заданы. Это численные матрица и вектор правых частей.
Если расписать (7) по правилам умножения матриц на вектор (4), то это и есть система линейных уравнений (СЛАУ). Не нужно, наверно, объяснять, почему система, почему уравнений, и почему линейных. Скажем только, что запись в виде (7) общепринята. Пусть в матрице n строк и m столбцов. Т.е. имеется система из n уравнений с m неизвестными. Причём n и m могут быть любыми, но, конечно, целыми числами.
Тот, кому довелось хотя бы раз решать систему из 3х уравнений ( не дай бог из пяти) с нецелыми коэффициентами по формулам Крамера, знает какой это труд. (недаром преподаватели математики дают домой студентам задачи линейного программирования с матрицами больше пяти). Если же решать систему (4) для квадратных матриц 100*100, то в этом методе придётся вычислять определитель матрицы Асотого порядка.Для этого придётся выполнить 100! умножений. Это примерно 10157 умножений. Да ещё столько же сложений. Ясно, что это абсолютно бессмысленное мероприятие. Поэтому не следует думать, что большие системы решались давно.
Прогресс в этом предприятии начался с 1828г., когда К.Гаусс дал численный метод решения определённых систем линейных алгебраических уравнений (СЛАУ). Интересно проследить за ростом сложности этих задач. В книге Х.Д.Икрамова (1987г.) приводятся такие данные. За период с 1828г т.е. от Гаусса, по 1974г. по тематике СЛАУ было опубликовано 4000 научных работ, с1974 по 1980 – 3000 работ и за три года до 1984г. 4000 публикаций. Крупнейший авторитет в этой области Д.Уилкинсон вспоминает, что во время второй мировой войны он получил от военного ведомства ответственное задание: решить систему из 12 уравнений, а уже после войны в Национальной физической лаборатории (Англия) для решения задачи из 18 уравнений была организована группа из четырёх математиков, в которую он снова входил. И ещё там был Алан Тьюринг. Но уже в 1974г. Национальная геодезическая служба США объявила о некотором проекте, в котором решалась задача 6 000 000 уравнений с 400 000 неизвестными по методу МНК. Проект был рассчитан на 10 лет. Так выросли потребности и вычислительные возможности. Решение систем линейных уравнений – это фундамент современной вычислительной математики.
Классическим решением системы (СЛАУ) называется такой численный вектор x, который после подстановки в (7) обращает его в тождество. Система называется совместной, если она имеет решение. В противном случае она называется противоречивой. Систем называется однородной, если b=0.
Известно, что не все системы имеют решение. Известно также, что системы могут иметь много решений. Ясность в этот вопрос внесла теорема Кронекера-Капелли. Назовём расширенной матрицей системы матрицу А с присоединённым к ней справа столбцом свободных членов b,т.е.(А, b).
Теорема Кронекера-Капелли утверждает, что система совместна, если ранг матрицы системы равен рангу матрицы расширенной системы.
rang(A)= rang(A,b) (8)
В противном случае система противоречива.
Следствие 1: если количество уравнений равно количеству неизвестных (n=m) и система совместна, то она имеет единственное решение. В этом случае необходимо и достаточно, чтобы детерминант матрицы системы был не равен нулю det(A)≠0. Если система однородна и количество уравнений равно количеству неизвестных (n=m) и система совместна, то она имеет только нулевое решение (x=0). Такое решение называется тривиальным. Из этого вытекает ещё одна, широко используемая в теории линейной алгебры теорема: для того чтобы однородная система имела не тривиальное решение необходимо и достаточно, чтобы det(A)=0.
Следствие 2:если количество уравнений меньше количества неизвестных (n<m) и система совместна, то она имеет бесконечное множество решений. Такая система называется недоопределённой. Заниматься на практике решением недоопределённых систем не имеет смысла. Такие системы имеют бесчисленное множество решений. В экономике и технике, они считаются плохо поставленными.
В случае (n>m) система называется переопределённой. Такая система, вообще говоря, несовместна и не решается. Но такая ситуация складывается практически всегда в обработке результатов эксперимента по методу наименьших квадратов (МНК). Поэтому заниматься такими системами приходится очень часто. Это задача оптимизации. Дальше мы займёмся её решением.
Теперь о погрешностях. «Точные» системы и решения бывают только в средней школе. Зачастую системы, которые приходится решать в предметной области, не похожи на абстрактные математические системы. Это от того, что в матрице А и в векторе bвсегда имеются погрешности. Эти погрешности неустранимы и называются наследственными. Следовательно, решается (на ЭВМ или как-то) не математическая задача (7) с точными данными, а физическая задача, описываемая математической моделью
Ã*x’= ß. (9)
где матричные элементы (Ã)ij и ßi имеют погрешности. Поскольку это векторы и матрицы, оценка погрешности может быть дана только нормами ||∆Ã||≤ εA и ||∆ß ||≤ εß.
Таким образом, физическая задача описывается целым классом уравнений (9) и за решение её может быть взято любое из них, удовлетворяющее указанным неравенствам для погрешностей. Что мы ожидаем от решения? Прежде всего, мы хотим, чтобы решение непрерывно зависело от исходных данных. Это значит, что при малых изменениях ||∆Ã||≤ εA и ||∆ß ||≤ εß , решение тоже изменялось немного, а не скачком. Второе, чтобы решение было единственным. Отыскание такого решения называется корректно поставленной задачей. Не все задачи корректны. Некорректные задачи мы рассматривать не будем. Оказывается, что задача будет корректной тогда, когда выполняются условия:
|| ΔA|| || A-1|| < 1 (10)
Например, задача отыскания классического решения системы
25x1-36x2=1, 16x1-23x2= -1
с приближёнными исходными данными будет корректной при условии
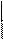
 || ΔA||≤0.02. Действительно, A-1 = -23 36
|| ΔA||≤0.02. Действительно, A-1 = -23 36
-16 25
и || A-1||2 =(∑∑|xi,j|2)0.5=5
Но даже для корректно поставленных задач, ясно, что в процессе «перелопачивания» чисел в алгоритме решения наследственные погрешности распространятся и на само решение (ответ), причём проследить за их распространением нет никакой возможности. Ведь уравнений могут быть сотни и это система уравнений. Т.е всё зависит от всего. Оценить величину результирующей погрешности можно только по норме ||∆x|| = ||x- x’||. Если, конечно, известно точное решение. А если оно неизвестно, то ||∆x|| - это оценка величины разброса решения. Если учитываются только погрешности в векторе bили только в матрице Ã,то формулы для относительной погрешности имеют вид:
||δx|| ≤ ||Ã||* ||Ã-1||* ||δß||
||δx|| ≤ ||Ã||* ||Ã-1||*||δÃ||(10)
В общем случае они сложнее.
Как видно, величина погрешности решения зависит в обеих формулах от величины Cond(A) = ||Ã||* ||Ã-1||. Эта величина называется числом обусловленности матрицы СЛАУ.
Если Cond(A) невелико, то матрица системы называется хорошо обусловленной и решение задачи в этом случае будет непрерывно зависеть от малых погрешностей в исходных данных. В противном случае, всё будет значительно хуже. При малых изменениях в исходных данных можно получить произвольные решения. Решать такие системы тоже не имеет большого смысла.
Но обусловленность - это только часть проблемы СЛАУ. Дело в том, что при машинном решении задачи по выбранному алгоритму числа при арифметических действиях над ними в ячейках машины округляются. Это вносит дополнительную погрешность. При мегафлопах в секунду она может накапливаться сильно, а может и не очень. Это зависит от свойств алгоритма. Алгоритмы могут быть устойчивыми или не устойчивыми к ошибкам округления. Поэтому нужно выбирать хорошие алгоритмы.
Таким образом, по указанным причинам и той роли СЛАУ в численных методах, задача решения системы СЛАУ – это фундаментальная задача вычислительной математики. Но так или иначе, абсолютной уверенности в том, что мы получили решение именно той задачи, которую хотели решить, у пользователя никогда нет.
Вот так углубилась простенькая тема погрешностей, которой мы слегка коснулись, когда рассматривали задачу о вписанном в угол шаровом контейнере. Вспомните, там всё тоже самое. Только проще и без компьютера. Там мы получили хорошие рекомендации к действиям. А здесь? Нужно тщательно анализировать и решение и алгоритм и постановку исходной задачи. Потому что, человек может ошибаться, но только компьютер, делая мегафлопы операций в секунду, может запутать всё окончательно. Не вникая в тонкости можно получить решение, но в нём может не оказаться ничего, кроме погрешностей.
Зачем мы об этом так подробно говорили? Можно было бы привести много доводов о необходимости этого, но лучше перечитайте выше приведённый текст со стр.12. И ещё дело в том, что решение уравнений это основная задача вычислительной математики и она рано или поздно встретится на каком-то шаге алгоритма оптимизации. И тогда все эти трудности могут проявиться. У нас это может произойти таким образом:
Пусть есть задача оптимизации f(x)-à min. Все «приличные» функции вблизи минимума похожи на вогнутые (или выпуклые) многомерные чашечки. Чтобы найти этот минимум, представим приближённо f(x) в окрестности минимума в виде квадратичного ряда Тейлора. В матричных обозначениях
f(x)=f(x0) + b*x+ ½ *x*A(x0)*x. (11)
Условие минимума есть: f’(x)=0. Дифференцируя (11) по компонентам x и приравнивая производные к нулю, как раз получим линейную систему A*x+b=0. Здесь A симметричная матрица вторых производных от f(x), а вектор b –это градиент функции f(x).
Вопросы для самопроверки:
Можно ли построить для реального объекта задачу, имеющую точное решение?
Чем характеризуется некорректно поставленная задача?
Что характеризует число обусловленности СЛАУ ?
Какова геометрическая интерпретация плохо обусловленной задачи СЛАУ?
Чему равняется длина вектора (1, 1, 1) в базисе (i,j,k).Чему она равна в другом каком-нибудь другом базисе?